Entscheidungsgrenzen von multinomialer und One-vs-Rest Logistischer Regression

Dieses Beispiel vergleicht die Entscheidungsgrenzen von multinomialer und One-vs-Rest Logistischer Regression auf einem 2D-Datensatz mit drei Klassen.

Wir vergleichen die Entscheidungsgrenzen beider Methoden, was dem Aufruf der Methode predict entspricht. Zusätzlich plotten wir die Hyperebenen, die der Linie entsprechen, bei der die Wahrscheinlichkeitsschätzung für eine Klasse 0,5 beträgt.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datensatzgenerierung

Wir generieren einen synthetischen Datensatz mit der Funktion make_blobs. Der Datensatz besteht aus 1.000 Stichproben aus drei verschiedenen Klassen, die um [-5, 0], [0, 1.5] und [5, -1] zentriert sind. Nach der Generierung wenden wir eine lineare Transformation an, um eine gewisse Korrelation zwischen den Merkmalen einzuführen und das Problem schwieriger zu gestalten. Dies ergibt einen 2D-Datensatz mit drei überlappenden Klassen, der sich gut zur Demonstration der Unterschiede zwischen multinomialer und One-vs-Rest Logistischer Regression eignet.

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_blobs

centers = [[-5, 0], [0, 1.5], [5, -1]]
X, y = make_blobs(n_samples=1_000, centers=centers, random_state=40)
transformation = [[0.4, 0.2], [-0.4, 1.2]]
X = np.dot(X, transformation)

fig, ax = plt.subplots(figsize=(6, 4))

scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="black")
ax.set(title="Synthetic Dataset", xlabel="Feature 1", ylabel="Feature 2")
_ = ax.legend(*scatter.legend_elements(), title="Classes")

Klassifikatortraining

Wir trainieren zwei verschiedene logistische Regressionsklassifikatoren: multinomial und One-vs-Rest. Der multinomiale Klassifikator verarbeitet alle Klassen gleichzeitig, während der One-vs-Rest-Ansatz für jede Klasse einen binären Klassifikator gegen alle anderen trainiert.

from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier

logistic_regression_multinomial = LogisticRegression().fit(X, y)
logistic_regression_ovr = OneVsRestClassifier(LogisticRegression()).fit(X, y)

accuracy_multinomial = logistic_regression_multinomial.score(X, y)
accuracy_ovr = logistic_regression_ovr.score(X, y)

Visualisierung der Entscheidungsgrenzen

Visualisieren wir die Entscheidungsgrenzen beider Modelle, die von der Methode predict der Klassifikatoren bereitgestellt werden.

from sklearn.inspection import DecisionBoundaryDisplay

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)

for model, title, ax in [
    (
        logistic_regression_multinomial,
        f"Multinomial Logistic Regression\n(Accuracy: {accuracy_multinomial:.3f})",
        ax1,
    ),
    (
        logistic_regression_ovr,
        f"One-vs-Rest Logistic Regression\n(Accuracy: {accuracy_ovr:.3f})",
        ax2,
    ),
]:
    DecisionBoundaryDisplay.from_estimator(
        model,
        X,
        ax=ax,
        response_method="predict",
        alpha=0.8,
    )
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k")
    legend = ax.legend(*scatter.legend_elements(), title="Classes")
    ax.add_artist(legend)
    ax.set_title(title)

Wir sehen, dass die Entscheidungsgrenzen unterschiedlich sind. Dieser Unterschied ergibt sich aus ihren Ansätzen

• Die multinomiale logistische Regression berücksichtigt bei der Optimierung alle Klassen gleichzeitig.

• Die One-vs-Rest logistische Regression passt jede Klasse unabhängig von den anderen an.

Diese unterschiedlichen Strategien können zu variierenden Entscheidungsgrenzen führen, insbesondere bei komplexen Mehrklassenproblemen.

Visualisierung der Hyperebenen

Wir visualisieren auch die Hyperebenen, die der Linie entsprechen, bei der die Wahrscheinlichkeitsschätzung für eine Klasse 0,5 beträgt.

def plot_hyperplanes(classifier, X, ax):
    xmin, xmax = X[:, 0].min(), X[:, 0].max()
    ymin, ymax = X[:, 1].min(), X[:, 1].max()
    ax.set(xlim=(xmin, xmax), ylim=(ymin, ymax))

    if isinstance(classifier, OneVsRestClassifier):
        coef = np.concatenate([est.coef_ for est in classifier.estimators_])
        intercept = np.concatenate([est.intercept_ for est in classifier.estimators_])
    else:
        coef = classifier.coef_
        intercept = classifier.intercept_

    for i in range(coef.shape[0]):
        w = coef[i]
        a = -w[0] / w[1]
        xx = np.linspace(xmin, xmax)
        yy = a * xx - (intercept[i]) / w[1]
        ax.plot(xx, yy, "--", linewidth=3, label=f"Class {i}")

    return ax.get_legend_handles_labels()

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)

for model, title, ax in [
    (
        logistic_regression_multinomial,
        "Multinomial Logistic Regression Hyperplanes",
        ax1,
    ),
    (logistic_regression_ovr, "One-vs-Rest Logistic Regression Hyperplanes", ax2),
]:
    hyperplane_handles, hyperplane_labels = plot_hyperplanes(model, X, ax)
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k")
    scatter_handles, scatter_labels = scatter.legend_elements()

    all_handles = hyperplane_handles + scatter_handles
    all_labels = hyperplane_labels + scatter_labels

    ax.legend(all_handles, all_labels, title="Classes")
    ax.set_title(title)

plt.show()

Während die Hyperebenen für die Klassen 0 und 2 zwischen den beiden Methoden recht ähnlich sind, stellen wir fest, dass die Hyperebene für Klasse 1 deutlich anders ist. Dieser Unterschied ergibt sich aus den grundlegenden Ansätzen der One-vs-Rest und der multinomialen logistischen Regression.

Für die One-vs-Rest logistische Regression

• Jede Hyperebene wird unabhängig bestimmt, indem eine Klasse gegen alle anderen betrachtet wird.

• Für Klasse 1 stellt die Hyperebene die Entscheidungsgrenze dar, die Klasse 1 am besten von den kombinierten Klassen 0 und 2 trennt.

• Dieser binäre Ansatz kann zu einfacheren Entscheidungsgrenzen führen, erfasst aber möglicherweise keine komplexen Beziehungen zwischen allen Klassen gleichzeitig.

• Es gibt keine sinnvolle Interpretation der bedingten Klassenwahrscheinlichkeiten.

Für die multinomiale logistische Regression

• Alle Hyperebenen werden gleichzeitig bestimmt, wobei die Beziehungen zwischen allen Klassen auf einmal berücksichtigt werden.

• Die vom Modell minimisierte Verlustfunktion ist eine korrekte Scoring-Regel, was bedeutet, dass das Modell zur Schätzung der bedingten Klassenwahrscheinlichkeiten optimiert wird, die daher aussagekräftig sind.

• Jede Hyperebene stellt die Entscheidungsgrenze dar, bei der die Wahrscheinlichkeit einer Klasse höher wird als die anderen, basierend auf der gesamten Wahrscheinlichkeitsverteilung.

• Dieser Ansatz kann nuanciertere Beziehungen zwischen den Klassen erfassen und potenziell zu einer genaueren Klassifizierung bei Mehrklassenproblemen führen.

Der Unterschied bei den Hyperebenen, insbesondere für Klasse 1, unterstreicht, wie diese Methoden trotz ähnlicher Gesamtgenauigkeit unterschiedliche Entscheidungsgrenzen erzeugen können.

In der Praxis wird die Verwendung der multinomialen logistischen Regression empfohlen, da sie eine gut formulierte Verlustfunktion minimiert, was zu besser kalibrierten Klassenwahrscheinlichkeiten und damit zu interpretierbareren Ergebnissen führt. Was die Entscheidungsgrenzen betrifft, sollte man eine Nutzenfunktion formulieren, um die Klassenwahrscheinlichkeiten in eine sinnvolle Größe für das jeweilige Problem umzuwandeln. One-vs-Rest ermöglicht unterschiedliche Entscheidungsgrenzen, erlaubt aber keine feingranulare Steuerung des Kompromisses zwischen den Klassen, wie es eine Nutzenfunktion tun würde.

Verwandte Beispiele

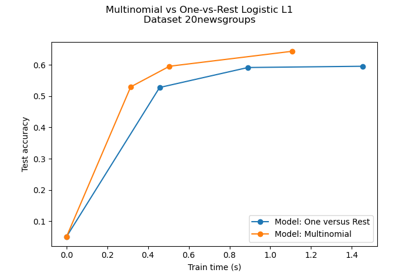
Multiklassen-Sparse-Logistische-Regression auf 20newgroups

Multiklassen-Sparse-Logistische-Regression auf 20newgroups

Klassifikationswahrscheinlichkeit plotten

Klassifikationswahrscheinlichkeit plotten

Restricted Boltzmann Machine Merkmale für Ziffernklassifikation

Restricted Boltzmann Machine Merkmale für Ziffernklassifikation

Multi-Klassen SGD auf dem Iris-Datensatz plotten

Multi-Klassen SGD auf dem Iris-Datensatz plotten