Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Tweedie-Regression bei Versicherungsansprüchen#
Dieses Beispiel illustriert die Verwendung von Poisson-, Gamma- und Tweedie-Regression auf dem Datensatz der französischen Kraftfahrzeug-Haftpflichtansprüche und ist von einem R-Tutorial inspiriert [1].
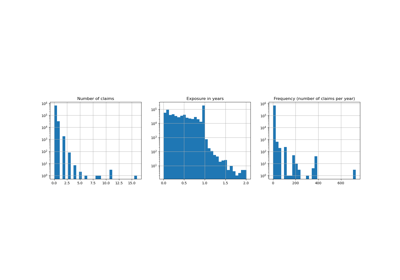
In diesem Datensatz entspricht jede Stichprobe einer Versicherungs police, d. h. einem Vertrag zwischen einer Versicherungsgesellschaft und einer Einzelperson (Versicherungsnehmer). Verfügbare Merkmale sind unter anderem das Alter des Fahrers, das Fahrzeugalter, die Fahrzeugleistung.
Einige Definitionen: Ein *Anspruch* ist die Aufforderung des Versicherungsnehmers an den Versicherer, eine durch die Versicherung gedeckte Leistung zu entschädigen. Der *Anspruchsbetrag* ist der Geldbetrag, den der Versicherer zahlen muss. Die *Exposition* ist die Dauer des Versicherungsschutzes einer bestimmten Police in Jahren.
Unser Ziel hier ist es, den Erwartungswert, d. h. den Mittelwert, des gesamten Anspruchsbetrags pro Expositionseinheit, auch als reiner Premium bezeichnet, vorherzusagen.
Dafür gibt es mehrere Möglichkeiten, zwei davon sind:
Das Anzahlen von Ansprüchen mit einer Poisson-Verteilung und den durchschnittlichen Anspruchsbetrag pro Anspruch, auch als Schwere bekannt, als Gamma-Verteilung modellieren und die Vorhersagen beider multiplizieren, um den gesamten Anspruchsbetrag zu erhalten.
Den gesamten Anspruchsbetrag pro Exposition direkt modellieren, typischerweise mit einer Tweedie-Verteilung mit Tweedie-Potenz \(p \in (1, 2)\).
In diesem Beispiel werden wir beide Ansätze illustrieren. Wir beginnen mit der Definition einiger Hilfsfunktionen zum Laden der Daten und zur Visualisierung der Ergebnisse.
from functools import partial
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.metrics import (
mean_absolute_error,
mean_squared_error,
mean_tweedie_deviance,
)
def load_mtpl2(n_samples=None):
"""Fetch the French Motor Third-Party Liability Claims dataset.
Parameters
----------
n_samples: int, default=None
number of samples to select (for faster run time). Full dataset has
678013 samples.
"""
# freMTPL2freq dataset from https://www.openml.org/d/41214
df_freq = fetch_openml(data_id=41214, as_frame=True).data
df_freq["IDpol"] = df_freq["IDpol"].astype(int)
df_freq.set_index("IDpol", inplace=True)
# freMTPL2sev dataset from https://www.openml.org/d/41215
df_sev = fetch_openml(data_id=41215, as_frame=True).data
# sum ClaimAmount over identical IDs
df_sev = df_sev.groupby("IDpol").sum()
df = df_freq.join(df_sev, how="left")
df["ClaimAmount"] = df["ClaimAmount"].fillna(0)
# unquote string fields
for column_name in df.columns[[t is object for t in df.dtypes.values]]:
df[column_name] = df[column_name].str.strip("'")
return df.iloc[:n_samples]
def plot_obs_pred(
df,
feature,
weight,
observed,
predicted,
y_label=None,
title=None,
ax=None,
fill_legend=False,
):
"""Plot observed and predicted - aggregated per feature level.
Parameters
----------
df : DataFrame
input data
feature: str
a column name of df for the feature to be plotted
weight : str
column name of df with the values of weights or exposure
observed : str
a column name of df with the observed target
predicted : DataFrame
a dataframe, with the same index as df, with the predicted target
fill_legend : bool, default=False
whether to show fill_between legend
"""
# aggregate observed and predicted variables by feature level
df_ = df.loc[:, [feature, weight]].copy()
df_["observed"] = df[observed] * df[weight]
df_["predicted"] = predicted * df[weight]
df_ = (
df_.groupby([feature])[[weight, "observed", "predicted"]]
.sum()
.assign(observed=lambda x: x["observed"] / x[weight])
.assign(predicted=lambda x: x["predicted"] / x[weight])
)
ax = df_.loc[:, ["observed", "predicted"]].plot(style=".", ax=ax)
y_max = df_.loc[:, ["observed", "predicted"]].values.max() * 0.8
p2 = ax.fill_between(
df_.index,
0,
y_max * df_[weight] / df_[weight].values.max(),
color="g",
alpha=0.1,
)
if fill_legend:
ax.legend([p2], ["{} distribution".format(feature)])
ax.set(
ylabel=y_label if y_label is not None else None,
title=title if title is not None else "Train: Observed vs Predicted",
)
def score_estimator(
estimator,
X_train,
X_test,
df_train,
df_test,
target,
weights,
tweedie_powers=None,
):
"""Evaluate an estimator on train and test sets with different metrics"""
metrics = [
("D² explained", None), # Use default scorer if it exists
("mean abs. error", mean_absolute_error),
("mean squared error", mean_squared_error),
]
if tweedie_powers:
metrics += [
(
"mean Tweedie dev p={:.4f}".format(power),
partial(mean_tweedie_deviance, power=power),
)
for power in tweedie_powers
]
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
y, _weights = df[target], df[weights]
for score_label, metric in metrics:
if isinstance(estimator, tuple) and len(estimator) == 2:
# Score the model consisting of the product of frequency and
# severity models.
est_freq, est_sev = estimator
y_pred = est_freq.predict(X) * est_sev.predict(X)
else:
y_pred = estimator.predict(X)
if metric is None:
if not hasattr(estimator, "score"):
continue
score = estimator.score(X, y, sample_weight=_weights)
else:
score = metric(y, y_pred, sample_weight=_weights)
res.append({"subset": subset_label, "metric": score_label, "score": score})
res = (
pd.DataFrame(res)
.set_index(["metric", "subset"])
.score.unstack(-1)
.round(4)
.loc[:, ["train", "test"]]
)
return res
Laden von Datensätzen, grundlegende Merkmalsextraktion und Zieldefinitionen#
Wir konstruieren den Datensatz freMTPL2, indem wir die Tabelle freMTPL2freq, die die Anzahl der Ansprüche (ClaimNb) enthält, mit der Tabelle freMTPL2sev, die den Anspruchsbetrag (ClaimAmount) für dieselben Policen-IDs (IDpol) enthält, verknüpfen.
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import (
FunctionTransformer,
KBinsDiscretizer,
OneHotEncoder,
StandardScaler,
)
df = load_mtpl2()
# Correct for unreasonable observations (that might be data error)
# and a few exceptionally large claim amounts
df["ClaimNb"] = df["ClaimNb"].clip(upper=4)
df["Exposure"] = df["Exposure"].clip(upper=1)
df["ClaimAmount"] = df["ClaimAmount"].clip(upper=200000)
# If the claim amount is 0, then we do not count it as a claim. The loss function
# used by the severity model needs strictly positive claim amounts. This way
# frequency and severity are more consistent with each other.
df.loc[(df["ClaimAmount"] == 0) & (df["ClaimNb"] >= 1), "ClaimNb"] = 0
log_scale_transformer = make_pipeline(
FunctionTransformer(func=np.log), StandardScaler()
)
column_trans = ColumnTransformer(
[
(
"binned_numeric",
KBinsDiscretizer(
n_bins=10, quantile_method="averaged_inverted_cdf", random_state=0
),
["VehAge", "DrivAge"],
),
(
"onehot_categorical",
OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"],
),
("passthrough_numeric", "passthrough", ["BonusMalus"]),
("log_scaled_numeric", log_scale_transformer, ["Density"]),
],
remainder="drop",
)
X = column_trans.fit_transform(df)
# Insurances companies are interested in modeling the Pure Premium, that is
# the expected total claim amount per unit of exposure for each policyholder
# in their portfolio:
df["PurePremium"] = df["ClaimAmount"] / df["Exposure"]
# This can be indirectly approximated by a 2-step modeling: the product of the
# Frequency times the average claim amount per claim:
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
df["AvgClaimAmount"] = df["ClaimAmount"] / np.fmax(df["ClaimNb"], 1)
with pd.option_context("display.max_columns", 15):
print(df[df.ClaimAmount > 0].head())
ClaimNb Exposure Area VehPower VehAge DrivAge BonusMalus VehBrand \
IDpol
139 1 0.75 F 7 1 61 50 B12
190 1 0.14 B 12 5 50 60 B12
414 1 0.14 E 4 0 36 85 B12
424 2 0.62 F 10 0 51 100 B12
463 1 0.31 A 5 0 45 50 B12
VehGas Density Region ClaimAmount PurePremium Frequency \
IDpol
139 'Regular' 27000 R11 303.00 404.000000 1.333333
190 'Diesel' 56 R25 1981.84 14156.000000 7.142857
414 'Regular' 4792 R11 1456.55 10403.928571 7.142857
424 'Regular' 27000 R11 10834.00 17474.193548 3.225806
463 'Regular' 12 R73 3986.67 12860.225806 3.225806
AvgClaimAmount
IDpol
139 303.00
190 1981.84
414 1456.55
424 5417.00
463 3986.67
Frequenzmodell – Poisson-Verteilung#
Die Anzahl der Ansprüche (ClaimNb) ist eine positive ganze Zahl (0 eingeschlossen). Daher kann dieses Ziel durch eine Poisson-Verteilung modelliert werden. Es wird angenommen, dass es sich um die Anzahl diskreter Ereignisse handelt, die mit einer konstanten Rate in einem gegebenen Zeitintervall (Exposure, in Jahren) auftreten. Hier modellieren wir die Frequenz y = ClaimNb / Exposure, die immer noch eine (skalierte) Poisson-Verteilung ist, und verwenden Exposure als sample_weight.
from sklearn.linear_model import PoissonRegressor
from sklearn.model_selection import train_test_split
df_train, df_test, X_train, X_test = train_test_split(df, X, random_state=0)
Denken wir daran, dass trotz der scheinbar großen Anzahl von Datenpunkten in diesem Datensatz die Anzahl der Auswertungspunkte, an denen der Anspruchsbetrag nicht null ist, ziemlich klein ist.
len(df_test)
169504
len(df_test[df_test["ClaimAmount"] > 0])
6237
Infolgedessen erwarten wir erhebliche Schwankungen bei unserer Auswertung nach zufälliger Neubildung der Trainings-Test-Aufteilung.
Die Parameter des Modells werden geschätzt, indem die Poisson-Devianz auf dem Trainingssatz über einen Newton-Solver minimiert wird. Einige der Merkmale sind kollinear (z. B. weil wir in der OneHotEncoder keine kategoriale Ebene fallen gelassen haben), wir verwenden eine schwache L2-Regularisierung, um numerische Probleme zu vermeiden.
glm_freq = PoissonRegressor(alpha=1e-4, solver="newton-cholesky")
glm_freq.fit(X_train, df_train["Frequency"], sample_weight=df_train["Exposure"])
scores = score_estimator(
glm_freq,
X_train,
X_test,
df_train,
df_test,
target="Frequency",
weights="Exposure",
)
print("Evaluation of PoissonRegressor on target Frequency")
print(scores)
Evaluation of PoissonRegressor on target Frequency
subset train test
metric
D² explained 0.0448 0.0427
mean abs. error 0.1379 0.1378
mean squared error 0.2441 0.2246
Beachten Sie, dass die auf dem Testdatensatz gemessene Punktzahl überraschenderweise besser ist als auf dem Trainingsdatensatz. Dies könnte spezifisch für diese zufällige Trainings-Test-Aufteilung sein. Eine ordnungsgemäße Kreuzvalidierung könnte uns helfen, die Stichprobenvariabilität dieser Ergebnisse zu bewerten.
Wir können beobachtete und vorhergesagte Werte visuell vergleichen, aggregiert nach dem Alter des Fahrers (DrivAge), dem Fahrzeugalter (VehAge) und dem Bonus-Malus-System der Versicherung (BonusMalus).
fig, ax = plt.subplots(ncols=2, nrows=2, figsize=(16, 8))
fig.subplots_adjust(hspace=0.3, wspace=0.2)
plot_obs_pred(
df=df_train,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_train),
y_label="Claim Frequency",
title="train data",
ax=ax[0, 0],
)
plot_obs_pred(
df=df_test,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[0, 1],
fill_legend=True,
)
plot_obs_pred(
df=df_test,
feature="VehAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 0],
fill_legend=True,
)
plot_obs_pred(
df=df_test,
feature="BonusMalus",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 1],
fill_legend=True,
)

Laut den beobachteten Daten ist die Unfallhäufigkeit bei Fahrern unter 30 Jahren höher und positiv mit der Variablen BonusMalus korreliert. Unser Modell ist in der Lage, dieses Verhalten weitgehend korrekt zu modellieren.
Schwere-Modell - Gamma-Verteilung#
Der durchschnittliche Anspruchsbetrag oder die Schwere (AvgClaimAmount) kann empirisch so gezeigt werden, dass er annähernd einer Gamma-Verteilung folgt. Wir passen ein GLM-Modell für die Schwere mit denselben Merkmalen wie das Frequenzmodell an.
Hinweis
Wir filtern
ClaimAmount == 0heraus, da die Gamma-Verteilung die Unterstützung auf \((0, \infty)\) hat, nicht auf \([0, \infty)\).Wir verwenden
ClaimNbalssample_weight, um Policen mit mehr als einem Anspruch zu berücksichtigen.
from sklearn.linear_model import GammaRegressor
mask_train = df_train["ClaimAmount"] > 0
mask_test = df_test["ClaimAmount"] > 0
glm_sev = GammaRegressor(alpha=10.0, solver="newton-cholesky")
glm_sev.fit(
X_train[mask_train.values],
df_train.loc[mask_train, "AvgClaimAmount"],
sample_weight=df_train.loc[mask_train, "ClaimNb"],
)
scores = score_estimator(
glm_sev,
X_train[mask_train.values],
X_test[mask_test.values],
df_train[mask_train],
df_test[mask_test],
target="AvgClaimAmount",
weights="ClaimNb",
)
print("Evaluation of GammaRegressor on target AvgClaimAmount")
print(scores)
Evaluation of GammaRegressor on target AvgClaimAmount
subset train test
metric
D² explained 3.900000e-03 4.400000e-03
mean abs. error 1.756752e+03 1.744055e+03
mean squared error 5.801775e+07 5.030676e+07
Diese Werte der Metriken sind nicht unbedingt leicht zu interpretieren. Es kann aufschlussreich sein, sie mit einem Modell zu vergleichen, das keine Eingabemerkmale verwendet und immer einen konstanten Wert vorhersagt, d. h. den durchschnittlichen Anspruchsbetrag, in derselben Einstellung.
from sklearn.dummy import DummyRegressor
dummy_sev = DummyRegressor(strategy="mean")
dummy_sev.fit(
X_train[mask_train.values],
df_train.loc[mask_train, "AvgClaimAmount"],
sample_weight=df_train.loc[mask_train, "ClaimNb"],
)
scores = score_estimator(
dummy_sev,
X_train[mask_train.values],
X_test[mask_test.values],
df_train[mask_train],
df_test[mask_test],
target="AvgClaimAmount",
weights="ClaimNb",
)
print("Evaluation of a mean predictor on target AvgClaimAmount")
print(scores)
Evaluation of a mean predictor on target AvgClaimAmount
subset train test
metric
D² explained 0.000000e+00 -0.000000e+00
mean abs. error 1.756687e+03 1.744497e+03
mean squared error 5.803882e+07 5.033764e+07
Wir kommen zu dem Schluss, dass der Anspruchsbetrag sehr schwer vorherzusagen ist. Dennoch ist der GammaRegressor in der Lage, einige Informationen aus den Eingabemerkmalen zu nutzen, um den Mittelwert-Baseline in Bezug auf D² geringfügig zu verbessern.
Beachten Sie, dass das resultierende Modell der durchschnittliche Anspruchsbetrag pro Anspruch ist. Als solches ist es bedingt auf mindestens einen Anspruch und kann nicht zur Vorhersage des durchschnittlichen Anspruchsbetrags pro Police verwendet werden. Dazu muss es mit einem Anspruchsfrequenzmodell kombiniert werden.
print(
"Mean AvgClaim Amount per policy: %.2f "
% df_train["AvgClaimAmount"].mean()
)
print(
"Mean AvgClaim Amount | NbClaim > 0: %.2f"
% df_train["AvgClaimAmount"][df_train["AvgClaimAmount"] > 0].mean()
)
print(
"Predicted Mean AvgClaim Amount | NbClaim > 0: %.2f"
% glm_sev.predict(X_train).mean()
)
print(
"Predicted Mean AvgClaim Amount (dummy) | NbClaim > 0: %.2f"
% dummy_sev.predict(X_train).mean()
)
Mean AvgClaim Amount per policy: 71.78
Mean AvgClaim Amount | NbClaim > 0: 1951.21
Predicted Mean AvgClaim Amount | NbClaim > 0: 1940.95
Predicted Mean AvgClaim Amount (dummy) | NbClaim > 0: 1978.59
Wir können beobachtete und vorhergesagte Werte visuell vergleichen, aggregiert für das Alter des Fahrers (DrivAge).
fig, ax = plt.subplots(ncols=1, nrows=2, figsize=(16, 6))
plot_obs_pred(
df=df_train.loc[mask_train],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_train[mask_train.values]),
y_label="Average Claim Severity",
title="train data",
ax=ax[0],
)
plot_obs_pred(
df=df_test.loc[mask_test],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_test[mask_test.values]),
y_label="Average Claim Severity",
title="test data",
ax=ax[1],
fill_legend=True,
)
plt.tight_layout()

Insgesamt hat das Alter des Fahrers (DrivAge) einen geringen Einfluss auf die Anspruchsschwere, sowohl bei beobachteten als auch bei vorhergesagten Daten.