1.8. Kreuzzerlegung#
Das Modul zur Kreuzzerlegung enthält **überwachte** Schätzer zur Dimensionsreduktion und Regression, die zur Familie der „Partial Least Squares“ gehören.
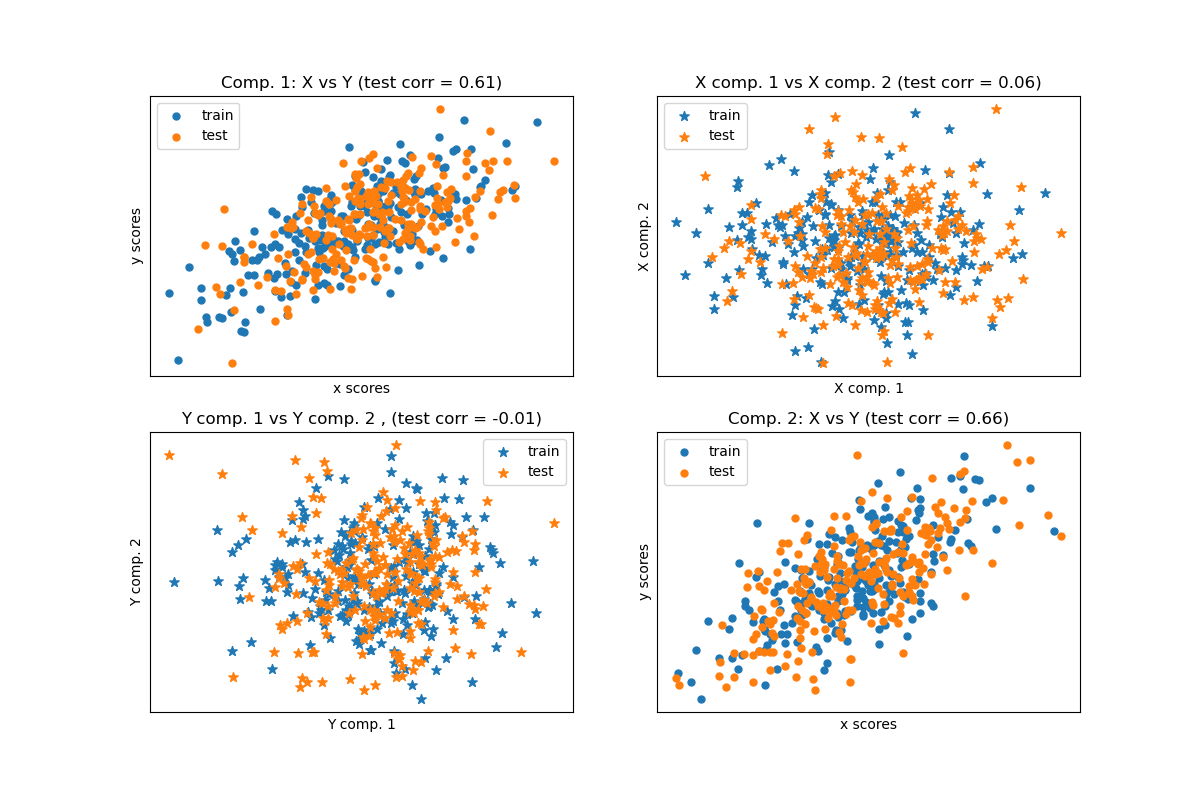
Algorithmen zur Kreuzzerlegung finden die grundlegenden Beziehungen zwischen zwei Matrizen (X und Y). Sie sind Ansätze mit latenten Variablen zur Modellierung der Kovarianzstrukturen in diesen beiden Räumen. Sie versuchen, die multidimensionale Richtung im X-Raum zu finden, die die maximale multidimensionale Varianzrichtung im Y-Raum erklärt. Mit anderen Worten, PLS projiziert sowohl X als auch Y in einen niederdimensionalen Unterraum, so dass die Kovarianz zwischen transformiert(X) und transformiert(Y) maximal ist.
PLS weist Ähnlichkeiten mit Principal Component Regression (PCR) auf, bei der die Stichproben zuerst in einen niederdimensionalen Unterraum projiziert werden und die Ziele y unter Verwendung von transformiert(X) vorhergesagt werden. Ein Problem bei PCR ist, dass die Dimensionsreduktion unüberwacht ist und einige wichtige Variablen verlieren kann: PCR würde die Merkmale mit der größten Varianz beibehalten, aber es ist möglich, dass Merkmale mit geringen Varianzen für die Vorhersage des Ziels relevant sind. In gewisser Weise ermöglicht PLS die gleiche Art von Dimensionsreduktion, aber unter Berücksichtigung der Ziele y. Eine Veranschaulichung dieser Tatsache findet sich im folgenden Beispiel: * Principal Component Regression vs Partial Least Squares Regression.
Abgesehen von CCA eignen sich die PLS-Schätzer besonders, wenn die Prädiktormatrix mehr Variablen als Beobachtungen hat und wenn Multikollinearität unter den Merkmalen besteht. Im Gegensatz dazu würde die Standard-Lineare Regression in diesen Fällen fehlschlagen, es sei denn, sie wird regularisiert.
Die in diesem Modul enthaltenen Klassen sind PLSRegression, PLSCanonical, CCA und PLSSVD
1.8.1. PLSCanonical#
Wir beschreiben hier den Algorithmus, der in PLSCanonical verwendet wird. Die anderen Schätzer verwenden Varianten dieses Algorithmus und werden unten detailliert beschrieben. Wir empfehlen Abschnitt [1] für weitere Details und Vergleiche zwischen diesen Algorithmen. In [1] entspricht PLSCanonical „PLSW2A“.
Gegeben seien zwei zentrierte Matrizen \(X \in \mathbb{R}^{n \times d}\) und \(Y \in \mathbb{R}^{n \times t}\) sowie eine Anzahl von Komponenten \(K\), dann geht PLSCanonical wie folgt vor:
Setze \(X_1\) auf \(X\) und \(Y_1\) auf \(Y\). Dann, für jedes \(k \in [1, K]\):
a) Berechne \(u_k \in \mathbb{R}^d\) und \(v_k \in \mathbb{R}^t\), die ersten linken und rechten Singulärvektoren der Kreuzkovarianzmatrix \(C = X_k^T Y_k\). \(u_k\) und \(v_k\) werden als *Gewichte* bezeichnet. Per Definition werden \(u_k\) und \(v_k\) so gewählt, dass sie die Kovarianz zwischen den projizierten \(X_k\) und dem projizierten Ziel maximieren, d.h. \(\text{Cov}(X_k u_k, Y_k v_k)\).
b) Projiziere \(X_k\) und \(Y_k\) auf die Singulärvektoren, um *Scores* zu erhalten: \(\xi_k = X_k u_k\) und \(\omega_k = Y_k v_k\).
c) Regrediere \(X_k\) auf \(\xi_k\), d.h. finde einen Vektor \(\gamma_k \in \mathbb{R}^d\), so dass die Rang-1-Matrix \(\xi_k \gamma_k^T\) so nah wie möglich an \(X_k\) liegt. Tue dasselbe auf \(Y_k\) mit \(\omega_k\), um \(\delta_k\) zu erhalten. Die Vektoren \(\gamma_k\) und \(\delta_k\) werden als *Loadings* bezeichnet.
d) *Deflationiere* \(X_k\) und \(Y_k\), d.h. subtrahiere die Rang-1-Approximationen: \(X_{k+1} = X_k - \xi_k \gamma_k^T\) und \(Y_{k + 1} = Y_k - \omega_k \delta_k^T\).
Am Ende haben wir \(X\) als Summe von Rang-1-Matrizen approximiert: \(X = \Xi \Gamma^T\), wobei \(\Xi \in \mathbb{R}^{n \times K}\) die Scores in seinen Spalten enthält und \(\Gamma^T \in \mathbb{R}^{K \times d}\) die Loadings in seinen Zeilen enthält. Ähnlich haben wir für \(Y\) \(Y = \Omega \Delta^T\).
Beachten Sie, dass die Score-Matrizen \(\Xi\) und \(\Omega\) den Projektionen der Trainingsdaten \(X\) bzw. \(Y\) entsprechen.
Schritt a) kann auf zwei Arten durchgeführt werden: Entweder durch Berechnung der gesamten SVD von \(C\) und Beibehaltung nur der Singulärvektoren mit den größten Singulärwerten, oder durch direkte Berechnung der Singulärvektoren mithilfe der Power-Iteration (vgl. Abschnitt 11.3 in [1]), was der Option 'nipals' des Parameters algorithm entspricht.
Daten transformieren#
Um \(X\) in \(\bar{X}\) zu transformieren, müssen wir eine Projektionsmatrix \(P\) finden, so dass \(\bar{X} = XP\). Wir wissen, dass für die Trainingsdaten \(\Xi = XP\) und \(X = \Xi \Gamma^T\) gilt. Wenn wir \(P = U(\Gamma^T U)^{-1}\) setzen, wobei \(U\) die Matrix mit den \(u_k\) in den Spalten ist, erhalten wir \(XP = X U(\Gamma^T U)^{-1} = \Xi (\Gamma^T U) (\Gamma^T U)^{-1} = \Xi\) wie gewünscht. Die Rotationsmatrix \(P\) kann über das Attribut x_rotations_ abgerufen werden.
Ähnlich kann \(Y\) mithilfe der Rotationsmatrix \(V(\Delta^T V)^{-1}\) transformiert werden, die über das Attribut y_rotations_ abgerufen werden kann.
Vorhersage der Ziele Y#
Um die Ziele von einigen Daten \(X\) vorherzusagen, suchen wir eine Koeffizientenmatrix \(\beta \in R^{d \times t}\), so dass \(Y = X\beta\) gilt.
Die Idee ist, die transformierten Ziele \(\Omega\) als Funktion der transformierten Stichproben \(\Xi\) vorherzusagen, indem \(\alpha \in \mathbb{R}\) berechnet wird, so dass \(\Omega = \alpha \Xi\).
Dann haben wir \(Y = \Omega \Delta^T = \alpha \Xi \Delta^T\), und da \(\Xi\) die transformierten Trainingsdaten sind, gilt \(Y = X \alpha P \Delta^T\), und als Ergebnis ist die Koeffizientenmatrix \(\beta = \alpha P \Delta^T\).
\(\beta\) kann über das Attribut coef_ abgerufen werden.
1.8.2. PLSSVD#
PLSSVD ist eine vereinfachte Version von PLSCanonical, wie oben beschrieben: Anstatt die Matrizen \(X_k\) und \(Y_k\) iterativ zu deflatieren, berechnet PLSSVD die SVD von \(C = X^TY\) nur *einmal* und speichert die n_components Singulärvektoren, die den größten Singulärwerten entsprechen, in den Matrizen U und V, die den Attributen x_weights_ und y_weights_ entsprechen. Hier sind die transformierten Daten einfach transformiert(X) = XU und transformiert(Y) = YV.
Wenn n_components == 1, sind PLSSVD und PLSCanonical strikt äquivalent.
1.8.3. PLSRegression#
Der Schätzer PLSRegression ist ähnlich zu PLSCanonical mit algorithm='nipals', mit 2 signifikanten Unterschieden:
In Schritt a) der Power-Iteration zur Berechnung von \(u_k\) und \(v_k\) wird \(v_k\) nie normalisiert.
In Schritt c) werden die Ziele \(Y_k\) mithilfe der Projektion von \(X_k\) (d.h. \(\xi_k\)) statt der Projektion von \(Y_k\) (d.h. \(\omega_k\)) approximiert. Mit anderen Worten, die Berechnung der Loadings ist anders. Infolgedessen wird auch die Deflation in Schritt d) beeinflusst.
Diese beiden Modifikationen beeinflussen die Ausgabe von predict und transform, die nicht dieselben sind wie bei PLSCanonical. Außerdem ist, während die Anzahl der Komponenten bei PLSCanonical durch min(n_samples, n_features, n_targets) begrenzt ist, hier die Grenze der Rang von \(X^TX\) ist, d.h. min(n_samples, n_features).
PLSRegression ist auch als PLS1 (einzelne Ziele) und PLS2 (mehrere Ziele) bekannt. Ähnlich wie Lasso ist PLSRegression eine Form der regularisierten linearen Regression, bei der die Anzahl der Komponenten die Stärke der Regularisierung steuert.
1.8.4. Canonical Correlation Analysis#
Canonical Correlation Analysis wurde vor PLS und unabhängig davon entwickelt. Es stellt sich jedoch heraus, dass CCA ein Spezialfall von PLS ist und in der Literatur dem PLS im „Modus B“ entspricht.
CCA unterscheidet sich von PLSCanonical in der Art und Weise, wie die Gewichte \(u_k\) und \(v_k\) in der Power-Iteration von Schritt a) berechnet werden. Details finden Sie in Abschnitt 10 von [1].
Da CCA die Invertierung von \(X_k^TX_k\) und \(Y_k^TY_k\) beinhaltet, kann dieser Schätzer instabil sein, wenn die Anzahl der Merkmale oder Ziele größer ist als die Anzahl der Stichproben.
Referenzen
Beispiele