2.6. Kovarianzschätzung#
Viele statistische Probleme erfordern die Schätzung der Kovarianzmatrix einer Grundgesamtheit, die als Schätzung der Form eines Streudiagramms eines Datensatzes betrachtet werden kann. Meistens muss eine solche Schätzung auf einer Stichprobe erfolgen, deren Eigenschaften (Größe, Struktur, Homogenität) einen großen Einfluss auf die Qualität der Schätzung haben. Das Paket sklearn.covariance bietet Werkzeuge zur genauen Schätzung der Kovarianzmatrix einer Grundgesamtheit in verschiedenen Szenarien.
Wir gehen davon aus, dass die Beobachtungen unabhängig und identisch verteilt (i.i.d.) sind.
2.6.1. Empirische Kovarianz#
Die Kovarianzmatrix eines Datensatzes wird gut durch den klassischen Maximum-Likelihood-Schätzer (oder „empirische Kovarianz“) approximiert, vorausgesetzt, die Anzahl der Beobachtungen ist im Verhältnis zur Anzahl der Merkmale (der die Beobachtungen beschreibenden Variablen) groß genug. Genauer gesagt, der Maximum-Likelihood-Schätzer einer Stichprobe ist ein asymptotisch unverzerrter Schätzer der entsprechenden Kovarianzmatrix der Grundgesamtheit.
Die empirische Kovarianzmatrix einer Stichprobe kann mit der Funktion empirical_covariance des Pakets berechnet werden, oder durch Anpassen eines Objekts EmpiricalCovariance an die Datensatzstichprobe mit der Methode EmpiricalCovariance.fit. Achten Sie darauf, dass die Ergebnisse davon abhängen, ob die Daten zentriert sind, sodass man den Parameter assume_centered korrekt verwenden möchte. Genauer gesagt, wenn assume_centered=True, dann sollten alle Merkmale in den Trainings- und Testdatensätzen einen Mittelwert von Null haben. Andernfalls sollten beide vom Benutzer zentriert werden, oder assume_centered=False verwendet werden.
Beispiele
Siehe Schrumpfende Kovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood für ein Beispiel, wie ein Objekt
EmpiricalCovariancean Daten angepasst wird.
2.6.2. Schrumpfende Kovarianz#
2.6.2.1. Grundlegende Schrumpfung#
Trotz der Tatsache, dass der Maximum-Likelihood-Schätzer ein asymptotisch unverzerrter Schätzer der Kovarianzmatrix ist, ist er kein guter Schätzer für die Eigenwerte der Kovarianzmatrix, sodass die Präzisionsmatrix, die sich aus seiner Inversion ergibt, nicht genau ist. Manchmal kann es sogar vorkommen, dass die empirische Kovarianzmatrix aus numerischen Gründen nicht invertiert werden kann. Um ein solches Inversionsproblem zu vermeiden, wurde eine Transformation der empirischen Kovarianzmatrix eingeführt: die shrinkage (Schrumpfung).
In scikit-learn kann diese Transformation (mit einem benutzerdefinierten Schrumpfungskoeffizienten) direkt auf eine vorab berechnete Kovarianz mit der Methode shrunk_covariance angewendet werden. Außerdem kann ein geschrumpfter Schätzer der Kovarianz mit einem Objekt ShrunkCovariance und dessen Methode ShrunkCovariance.fit an Daten angepasst werden. Auch hier hängen die Ergebnisse davon ab, ob die Daten zentriert sind, sodass man den Parameter assume_centered korrekt verwenden möchte.
Mathematisch gesehen besteht diese Schrumpfung darin, das Verhältnis zwischen den kleinsten und größten Eigenwerten der empirischen Kovarianzmatrix zu verringern. Dies kann durch einfaches Verschieben jedes Eigenwerts um einen gegebenen Offset erfolgen, was der Suche nach dem l2-penalisierten Maximum-Likelihood-Schätzer der Kovarianzmatrix entspricht. In der Praxis läuft die Schrumpfung auf eine einfache konvexe Transformation hinaus: \(\Sigma_{\rm shrunk} = (1-\alpha)\hat{\Sigma} + \alpha\frac{{\rm Tr}\hat{\Sigma}}{p}\rm Id\).
Die Wahl des Schrumpfungsgrads, \(\alpha\), entspricht der Festlegung eines Bias/Varianz-Trade-offs und wird im Folgenden erörtert.
Beispiele
Siehe Schrumpfende Kovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood für ein Beispiel, wie ein Objekt
ShrunkCovariancean Daten angepasst wird.
2.6.2.2. Ledoit-Wolf-Schrumpfung#
In ihrer Arbeit aus dem Jahr 2004 [1] schlagen O. Ledoit und M. Wolf eine Formel zur Berechnung des optimalen Schrumpfungskoeffizienten \(\alpha\) vor, die den mittleren quadratischen Fehler zwischen dem geschätzten und dem tatsächlichen Kovarianzmatrix minimiert.
Der Ledoit-Wolf-Schätzer der Kovarianzmatrix kann mit der Funktion ledoit_wolf des Pakets sklearn.covariance für eine Stichprobe berechnet werden, oder er kann alternativ durch Anpassen eines Objekts LedoitWolf an dieselbe Stichprobe erhalten werden.
Hinweis
Fall, in dem die Kovarianzmatrix der Grundgesamtheit isotrop ist
Es ist wichtig zu beachten, dass, wenn die Anzahl der Stichproben viel größer ist als die Anzahl der Merkmale, keine Schrumpfung erforderlich sein dürfte. Die Intuition dahinter ist, dass, wenn die Kovarianz der Grundgesamtheit vollen Rang hat, die Stichprobenkovarianz bei wachsender Anzahl von Stichproben ebenfalls positiv definit wird. Folglich wäre keine Schrumpfung erforderlich und die Methode sollte dies automatisch tun.
Dies ist jedoch im Ledoit-Wolf-Verfahren nicht der Fall, wenn die Kovarianz der Grundgesamtheit ein Vielfaches der Einheitsmatrix ist. In diesem Fall nähert sich der Ledoit-Wolf-Schätzer der Kovarianzmatrix dem Wert 1 an, wenn die Anzahl der Stichproben zunimmt. Dies deutet darauf hin, dass der optimale Schätzer der Kovarianzmatrix im Sinne von Ledoit-Wolf ein Vielfaches der Einheitsmatrix ist. Da die Kovarianz der Grundgesamtheit bereits ein Vielfaches der Einheitsmatrix ist, ist die Ledoit-Wolf-Lösung tatsächlich ein vernünftiger Schätzer.
Beispiele
Siehe Schrumpfende Kovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood für ein Beispiel, wie ein Objekt
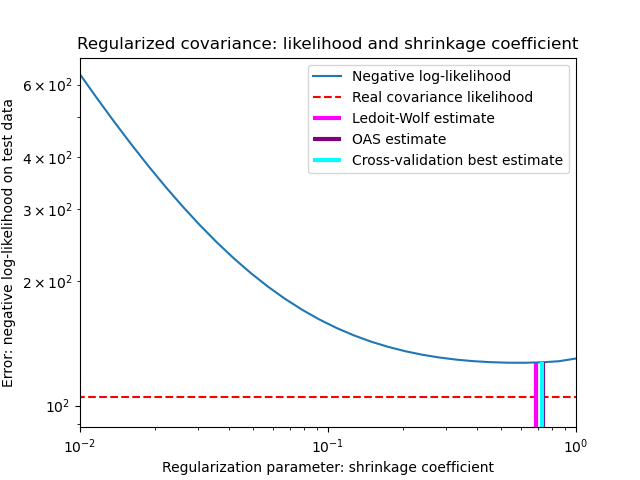
LedoitWolfan Daten angepasst wird und zur Visualisierung der Leistung des Ledoit-Wolf-Schätzers in Bezug auf die Likelihood.
Referenzen
2.6.2.3. Oracle Approximating Shrinkage (OAS)#
Unter der Annahme, dass die Daten gaußverteilt sind, leiteten Chen et al. [2] eine Formel ab, um einen Schrumpfungskoeffizienten zu wählen, der einen kleineren mittleren quadratischen Fehler ergibt als die von Ledoit und Wolf angegebene Formel. Der resultierende Schätzer ist als Oracle Shrinkage Approximating Estimator der Kovarianz bekannt.
Der OAS-Schätzer der Kovarianzmatrix kann mit der Funktion oas des Pakets sklearn.covariance für eine Stichprobe berechnet werden, oder er kann alternativ durch Anpassen eines Objekts OAS an dieselbe Stichprobe erhalten werden.
Bias-Varianz-Trade-off bei der Festlegung der Schrumpfung: Vergleich der Auswahl von Ledoit-Wolf- und OAS-Schätzern#
Referenzen
Beispiele
Siehe Schrumpfende Kovarianzschätzung: LedoitWolf vs OAS und Maximum-Likelihood für ein Beispiel, wie ein Objekt
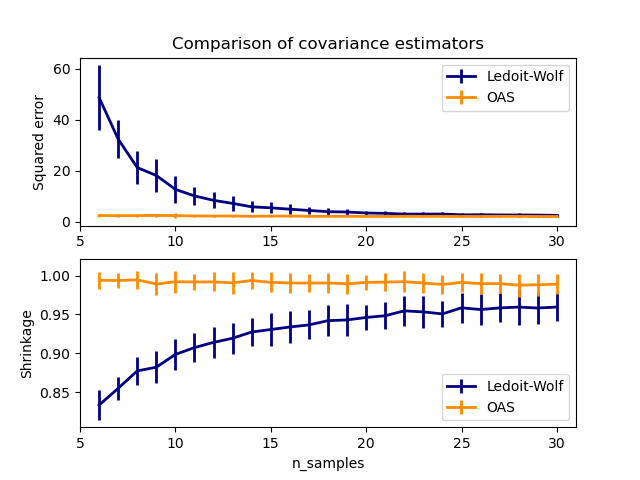
OASan Daten angepasst wird.Siehe Ledoit-Wolf vs OAS-Schätzung zur Visualisierung des Unterschieds im mittleren quadratischen Fehler zwischen einem
LedoitWolf- und einemOAS-Schätzer der Kovarianz.
2.6.3. Sparsity der inversen Kovarianz#
Die Inverse der Kovarianzmatrix, oft als Präzisionsmatrix bezeichnet, ist proportional zur partiellen Korrelationsmatrix. Sie gibt die bedingte Unabhängigkeitsbeziehung an. Anders ausgedrückt, wenn zwei Merkmale bedingt auf die anderen unabhängig sind, ist der entsprechende Koeffizient in der Präzisionsmatrix Null. Aus diesem Grund ist es sinnvoll, eine spärliche Präzisionsmatrix zu schätzen: Die Schätzung der Kovarianzmatrix wird besser konditioniert, indem Unabhängigkeitsbeziehungen aus den Daten gelernt werden. Dies wird als Kovarianzselektion bezeichnet.
In Situationen mit wenigen Stichproben, in denen n_samples in der Größenordnung von n_features oder kleiner ist, funktionieren spärliche inverse Kovarianzschätzer tendenziell besser als geschrumpfte Kovarianzschätzer. In der entgegengesetzten Situation oder bei sehr korrelierten Daten können sie jedoch numerisch instabil sein. Darüber hinaus sind spärliche Schätzer, im Gegensatz zu Schrumpfungsschätzern, in der Lage, off-diagonale Strukturen wiederherzustellen.
Der Schätzer GraphicalLasso verwendet eine l1-Strafe, um Sparsity auf die Präzisionsmatrix zu erzwingen: Je höher sein alpha-Parameter, desto spärlicher ist die Präzisionsmatrix. Das entsprechende Objekt GraphicalLassoCV verwendet Kreuzvalidierung, um den alpha-Parameter automatisch festzulegen.
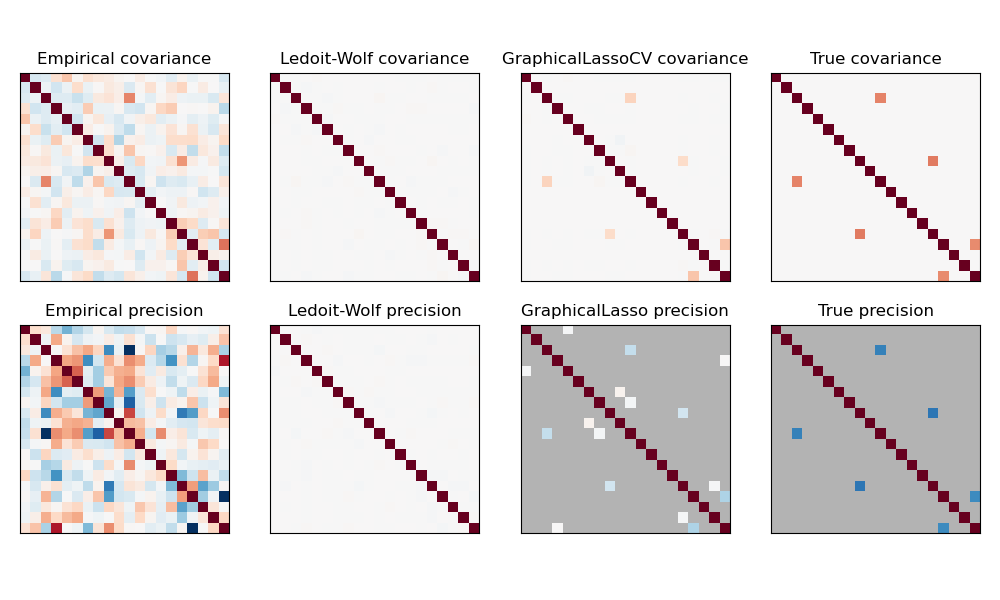
Ein Vergleich von Maximum-Likelihood-, Schrumpfungs- und spärlichen Schätzungen der Kovarianz- und Präzisionsmatrix in sehr kleinen Stichprobensettings.#
Hinweis
Strukturerkennung
Die Wiederherstellung einer grafischen Struktur aus Korrelationen in den Daten ist eine schwierige Aufgabe. Wenn Sie an einer solchen Wiederherstellung interessiert sind, beachten Sie Folgendes:
Die Wiederherstellung ist von einer Korrelationsmatrix einfacher als von einer Kovarianzmatrix: Standardisieren Sie Ihre Beobachtungen, bevor Sie
GraphicalLassoausführen.Wenn der zugrunde liegende Graph Knoten mit deutlich mehr Verbindungen als der Durchschnittsknoten hat, wird der Algorithmus einige dieser Verbindungen übersehen.
Wenn Ihre Anzahl an Beobachtungen im Vergleich zur Anzahl der Kanten in Ihrem zugrunde liegenden Graphen nicht groß ist, werden Sie ihn nicht wiederherstellen.
Selbst wenn Sie sich in günstigen Wiederherstellungsbedingungen befinden, führt der durch Kreuzvalidierung ausgewählte alpha-Parameter (z. B. mit dem Objekt
GraphicalLassoCV) dazu, dass zu viele Kanten ausgewählt werden. Die relevanten Kanten haben jedoch stärkere Gewichte als die irrelevanten.
Die mathematische Formulierung lautet:
Wobei \(K\) die zu schätzende Präzisionsmatrix und \(S\) die Stichprobenkovarianzmatrix ist. \(\|K\|_1\) ist die Summe der Absolutwerte der off-diagonalen Koeffizienten von \(K\). Der Algorithmus zur Lösung dieses Problems ist der GLasso-Algorithmus aus der Biostatistics-Arbeit von Friedman 2008. Es ist derselbe Algorithmus wie im R-Paket glasso.
Beispiele
Schätzung der spärlichen inversen Kovarianz: Beispiel anhand synthetischer Daten, das einige Wiederherstellungen einer Struktur zeigt und mit anderen Kovarianzschätzern vergleicht.
Visualisierung der Aktienmarktstruktur: Beispiel anhand echter Aktiendaten, das zeigt, welche Symbole am stärksten miteinander verknüpft sind.
Referenzen
Friedman et al, „Sparse inverse covariance estimation with the graphical lasso“, Biostatistics 9, S. 432, 2008
2.6.4. Robuste Kovarianzschätzung#
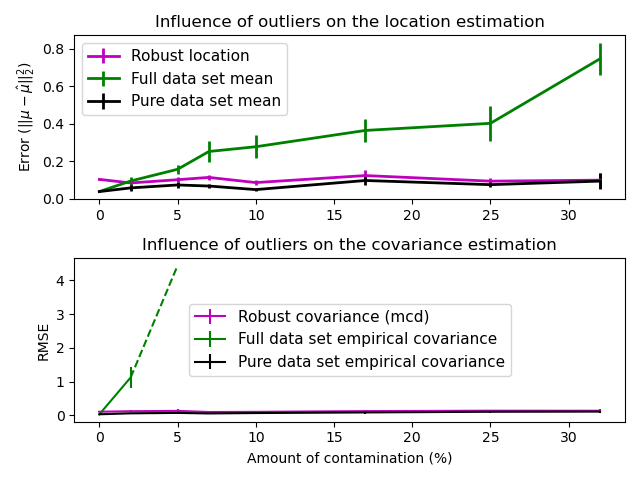
Reale Datensätze sind oft Mess- oder Aufzeichnungsfehlern ausgesetzt. Regelmäßige, aber ungewöhnliche Beobachtungen können ebenfalls aus verschiedenen Gründen auftreten. Sehr ungewöhnliche Beobachtungen werden als Ausreißer bezeichnet. Der empirische Kovarianzschätzer und die oben vorgestellten geschrumpften Kovarianzschätzer sind sehr empfindlich gegenüber dem Vorhandensein von Ausreißern in den Daten. Daher sollten für die Schätzung der Kovarianz realer Datensätze robuste Kovarianzschätzer verwendet werden. Alternativ können robuste Kovarianzschätzer zur Ausreißererkennung verwendet werden, um einige Beobachtungen für weitere Verarbeitungsschritte der Daten zu verwerfen/abzuwerten.
Das Paket sklearn.covariance implementiert einen robusten Kovarianzschätzer, den Minimum Covariance Determinant [3].
2.6.4.1. Minimum Covariance Determinant#
Der Minimum Covariance Determinant-Schätzer ist ein robuster Schätzer der Kovarianz eines Datensatzes, der 1984 von P.J. Rousseeuw eingeführt wurde [3]. Die Idee ist, einen bestimmten Anteil (h) an „guten“ Beobachtungen zu finden, die keine Ausreißer sind, und deren empirische Kovarianzmatrix zu berechnen. Diese empirische Kovarianzmatrix wird dann skaliert, um die durchgeführte Auswahl von Beobachtungen zu kompensieren („Konsistenzschritt“). Nach der Berechnung des Minimum Covariance Determinant-Schätzers können Beobachtungen entsprechend ihrer Mahalanobis-Distanz gewichtet werden, was zu einer neu gewichteten Schätzung der Kovarianzmatrix des Datensatzes führt („Neugewichtungsschritt“).
Rousseeuw und Van Driessen [4] entwickelten den FastMCD-Algorithmus zur Berechnung des Minimum Covariance Determinant. Dieser Algorithmus wird in scikit-learn beim Anpassen eines MCD-Objekts an Daten verwendet. Der FastMCD-Algorithmus berechnet gleichzeitig auch eine robuste Schätzung des Standorts des Datensatzes.
Rohe Schätzungen können als Attribute raw_location_ und raw_covariance_ eines robusten Kovarianzschätzerobjekts MinCovDet abgerufen werden.
Referenzen
P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass, 79:871, 1984.
A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS.
Beispiele
Siehe Robuste vs. empirische Kovarianzschätzung für ein Beispiel, wie ein Objekt
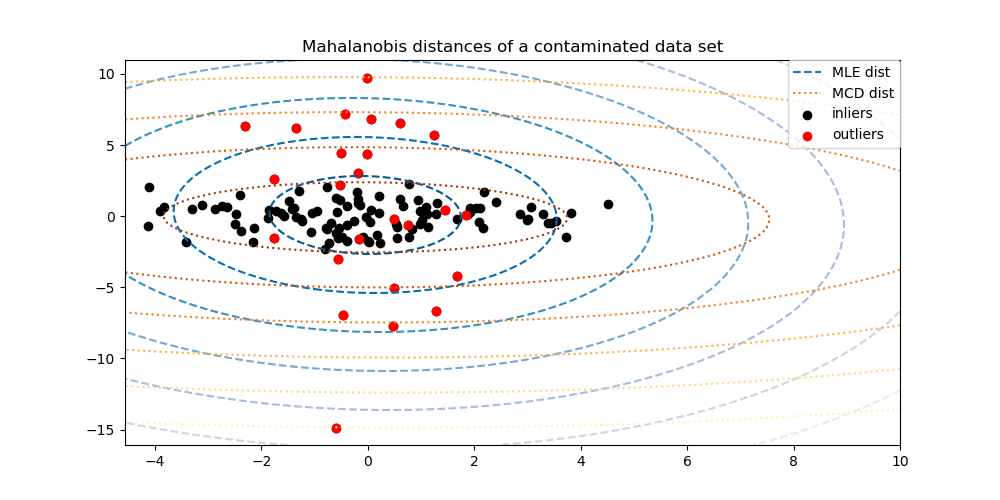
MinCovDetan Daten angepasst wird und wie die Schätzung trotz Ausreißern korrekt bleibt.Siehe Robuste Kovarianzschätzung und Relevanz von Mahalanobis-Distanzen zur Visualisierung des Unterschieds zwischen den Kovarianzschätzern
EmpiricalCovarianceundMinCovDetin Bezug auf die Mahalanobis-Distanz (wodurch wir auch eine bessere Schätzung der Präzisionsmatrix erhalten).