Hinweis

Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.

Schrumpfende Kovarianzschätzung: LedoitWolf vs. OAS und Maximum Likelihood#

Bei der Kovarianzschätzung ist der übliche Ansatz die Verwendung eines Maximum-Likelihood-Schätzers, wie z.B. des EmpiricalCovariance. Dieser ist unverzerrt, d.h. er konvergiert zur wahren (Populations-)Kovarianz, wenn viele Beobachtungen vorliegen. Es kann jedoch auch vorteilhaft sein, ihn zu regularisieren, um seine Varianz zu reduzieren; dies führt im Gegenzug zu einer gewissen Verzerrung. Dieses Beispiel illustriert die einfache Regularisierung, die in den Schrumpfende Kovarianz-Schätzern verwendet wird. Insbesondere konzentriert es sich darauf, wie die Höhe der Regularisierung eingestellt wird, d.h. wie der Bias-Varianz-Trade-off gewählt wird.

Referenzen

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Beispieldaten generieren#

import numpy as np

n_features, n_samples = 40, 20
np.random.seed(42)
base_X_train = np.random.normal(size=(n_samples, n_features))
base_X_test = np.random.normal(size=(n_samples, n_features))

# Color samples
coloring_matrix = np.random.normal(size=(n_features, n_features))
X_train = np.dot(base_X_train, coloring_matrix)
X_test = np.dot(base_X_test, coloring_matrix)

Berechnung der Likelihood auf Testdaten#

from scipy import linalg

from sklearn.covariance import ShrunkCovariance, empirical_covariance, log_likelihood

# spanning a range of possible shrinkage coefficient values
shrinkages = np.logspace(-2, 0, 30)
negative_logliks = [
    -ShrunkCovariance(shrinkage=s).fit(X_train).score(X_test) for s in shrinkages
]

# under the ground-truth model, which we would not have access to in real
# settings
real_cov = np.dot(coloring_matrix.T, coloring_matrix)
emp_cov = empirical_covariance(X_train)
loglik_real = -log_likelihood(emp_cov, linalg.inv(real_cov))

Vergleich verschiedener Ansätze zur Festlegung des Regularisierungsparameters#

Hier vergleichen wir 3 Ansätze

Einstellung des Parameters durch Kreuzvalidierung der Likelihood auf drei Folds gemäß einem Raster potenzieller Schrumpfungsparameter.
Eine geschlossene Formel von Ledoit und Wolf zur Berechnung des asymptotisch optimalen Regularisierungsparameters (Minimierung eines MSE-Kriteriums), die zu der LedoitWolf Kovarianzschätzung führt.
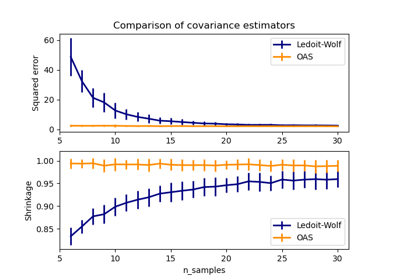
Eine Verbesserung der Ledoit-Wolf-Schrumpfung, die OAS, vorgeschlagen von Chen et al. [1]. Ihre Konvergenz ist unter der Annahme, dass die Daten Gaußsch sind, signifikant besser, insbesondere bei kleinen Stichproben.

from sklearn.covariance import OAS, LedoitWolf
from sklearn.model_selection import GridSearchCV

# GridSearch for an optimal shrinkage coefficient
tuned_parameters = [{"shrinkage": shrinkages}]
cv = GridSearchCV(ShrunkCovariance(), tuned_parameters)
cv.fit(X_train)

# Ledoit-Wolf optimal shrinkage coefficient estimate
lw = LedoitWolf()
loglik_lw = lw.fit(X_train).score(X_test)

# OAS coefficient estimate
oa = OAS()
loglik_oa = oa.fit(X_train).score(X_test)

Ergebnisse plotten#

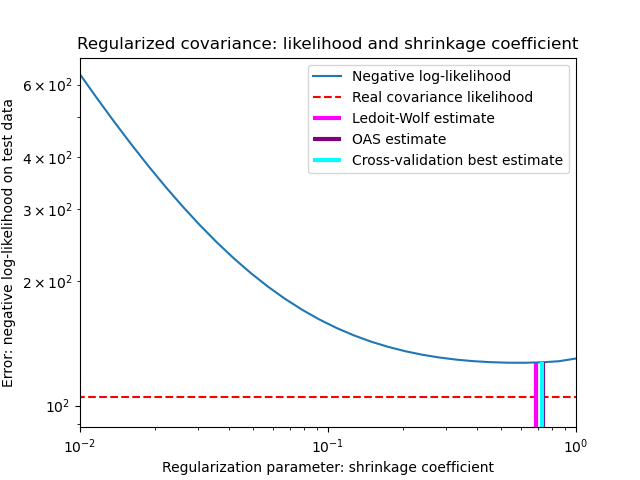
Zur Quantifizierung des Schätzfehlers zeichnen wir die Likelihood von ungesehenen Daten für verschiedene Werte des Schrumpfungsparameters auf. Wir zeigen auch die durch Kreuzvalidierung oder mit den LedoitWolf- und OAS-Schätzern gewählten Werte.

import matplotlib.pyplot as plt

fig = plt.figure()
plt.title("Regularized covariance: likelihood and shrinkage coefficient")
plt.xlabel("Regularization parameter: shrinkage coefficient")
plt.ylabel("Error: negative log-likelihood on test data")
# range shrinkage curve
plt.loglog(shrinkages, negative_logliks, label="Negative log-likelihood")

plt.plot(plt.xlim(), 2 * [loglik_real], "--r", label="Real covariance likelihood")

# adjust view
lik_max = np.amax(negative_logliks)
lik_min = np.amin(negative_logliks)
ymin = lik_min - 6.0 * np.log((plt.ylim()[1] - plt.ylim()[0]))
ymax = lik_max + 10.0 * np.log(lik_max - lik_min)
xmin = shrinkages[0]
xmax = shrinkages[-1]
# LW likelihood
plt.vlines(
    lw.shrinkage_,
    ymin,
    -loglik_lw,
    color="magenta",
    linewidth=3,
    label="Ledoit-Wolf estimate",
)
# OAS likelihood
plt.vlines(
    oa.shrinkage_, ymin, -loglik_oa, color="purple", linewidth=3, label="OAS estimate"
)
# best CV estimator likelihood
plt.vlines(
    cv.best_estimator_.shrinkage,
    ymin,
    -cv.best_estimator_.score(X_test),
    color="cyan",
    linewidth=3,
    label="Cross-validation best estimate",
)

plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.legend()

plt.show()

Regularized covariance: likelihood and shrinkage coefficient

Hinweis

Die Maximum-Likelihood-Schätzung entspricht keiner Schrumpfung und schneidet daher schlecht ab. Die Ledoit-Wolf-Schätzung schneidet sehr gut ab, da sie nahe am Optimum liegt und nicht rechenintensiv ist. In diesem Beispiel liegt die OAS-Schätzung etwas weiter zurück. Interessanterweise übertreffen beide Ansätze die Kreuzvalidierung, die deutlich rechenintensiver ist.

Gesamtlaufzeit des Skripts: (0 Minuten 0,391 Sekunden)

Verwandte Beispiele

Ledoit-Wolf vs OAS Schätzung

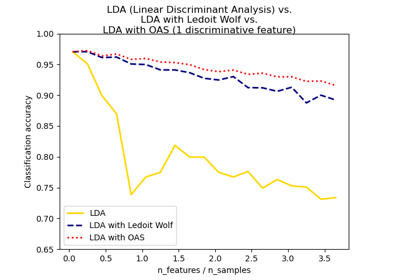
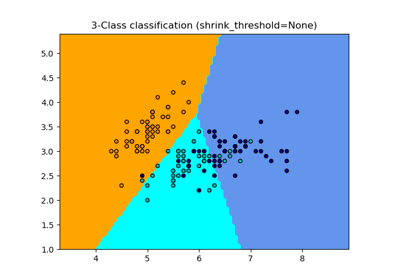
Normale, Ledoit-Wolf und OAS Lineare Diskriminanzanalyse zur Klassifikation

Nearest Centroid Klassifikation

Schwachstellen-Inverse Kovarianzschätzung

Galerie generiert von Sphinx-Gallery