t-SNE: Die Auswirkung verschiedener Perplexitätswerte auf die Form

Eine Veranschaulichung von t-SNE auf den Datensätzen mit zwei konzentrischen Kreisen und der S-Kurve für verschiedene Perplexitätswerte.

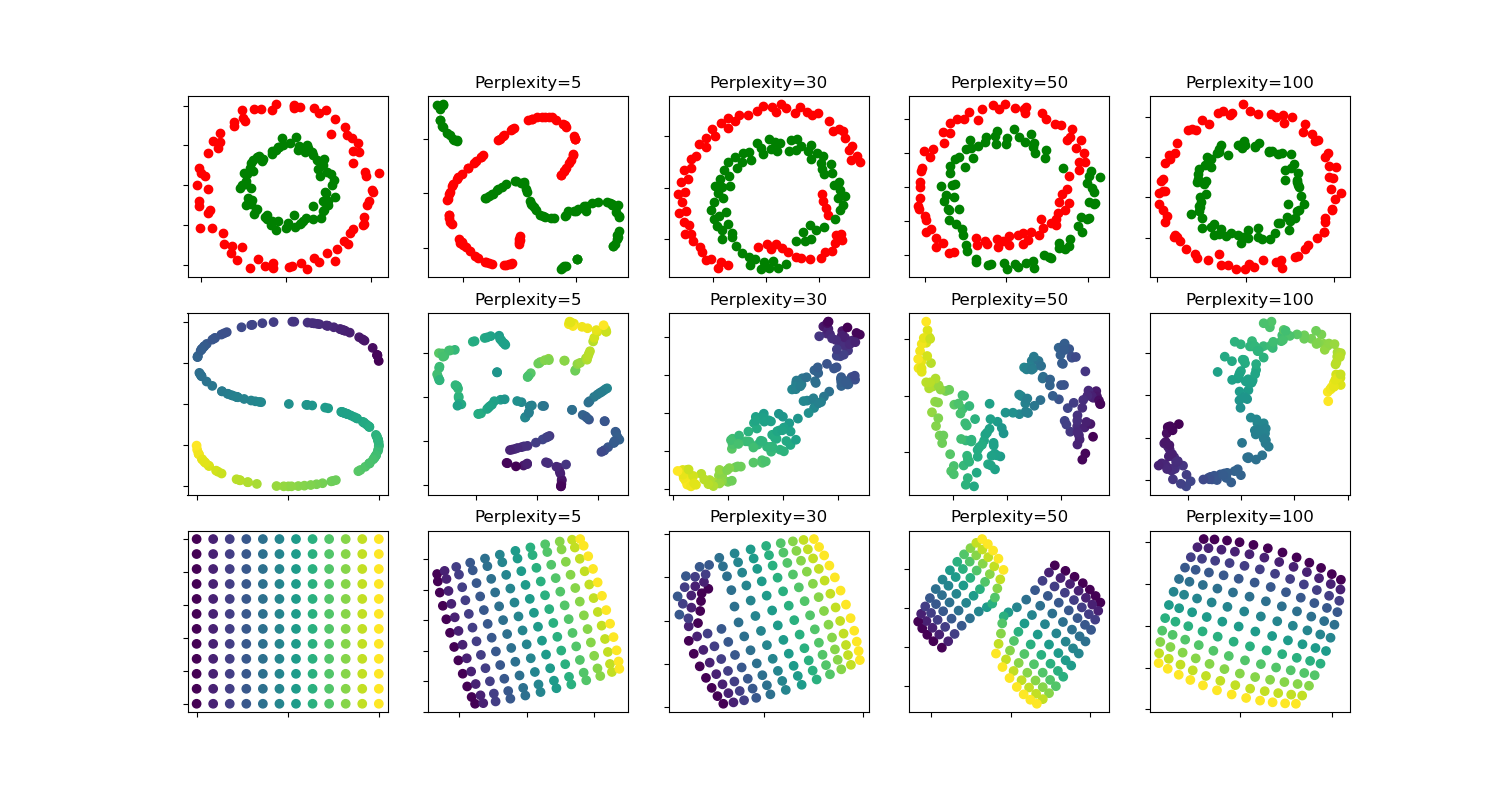
Wir beobachten eine Tendenz zu klareren Formen, wenn der Perplexitätswert steigt.

Die Größe, der Abstand und die Form von Clustern können sich je nach Initialisierung und Perplexitätswerten ändern und sind nicht immer aussagekräftig.

Wie unten gezeigt, findet t-SNE bei höheren Perplexitäten die aussagekräftige Topologie zweier konzentrischer Kreise. Die Größe und der Abstand der Kreise weichen jedoch leicht vom Original ab. Im Gegensatz zum Datensatz mit zwei Kreisen weichen die Formen auf dem S-Kurven-Datensatz selbst bei größeren Perplexitätswerten visuell von der S-Kurven-Topologie ab.

Für weitere Details bietet „How to Use t-SNE Effectively“ https://distill.pub/2016/misread-tsne/ eine gute Diskussion über die Auswirkungen verschiedener Parameter sowie interaktive Diagramme zur Erkundung dieser Auswirkungen.

circles, perplexity=5 in 0.13 sec
circles, perplexity=30 in 0.2 sec
circles, perplexity=50 in 0.23 sec
circles, perplexity=100 in 0.23 sec
S-curve, perplexity=5 in 0.13 sec
S-curve, perplexity=30 in 0.19 sec
S-curve, perplexity=50 in 0.23 sec
S-curve, perplexity=100 in 0.23 sec
uniform grid, perplexity=5 in 0.16 sec
uniform grid, perplexity=30 in 0.24 sec
uniform grid, perplexity=50 in 0.27 sec
uniform grid, perplexity=100 in 0.26 sec

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

from time import time

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import NullFormatter

from sklearn import datasets, manifold

n_samples = 150
n_components = 2
(fig, subplots) = plt.subplots(3, 5, figsize=(15, 8))
perplexities = [5, 30, 50, 100]

X, y = datasets.make_circles(
    n_samples=n_samples, factor=0.5, noise=0.05, random_state=0
)

red = y == 0
green = y == 1

ax = subplots[0][0]
ax.scatter(X[red, 0], X[red, 1], c="r")
ax.scatter(X[green, 0], X[green, 1], c="g")
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")

for i, perplexity in enumerate(perplexities):
    ax = subplots[0][i + 1]

    t0 = time()
    tsne = manifold.TSNE(
        n_components=n_components,
        init="random",
        random_state=0,
        perplexity=perplexity,
        max_iter=300,
    )
    Y = tsne.fit_transform(X)
    t1 = time()
    print("circles, perplexity=%d in %.2g sec" % (perplexity, t1 - t0))
    ax.set_title("Perplexity=%d" % perplexity)
    ax.scatter(Y[red, 0], Y[red, 1], c="r")
    ax.scatter(Y[green, 0], Y[green, 1], c="g")
    ax.xaxis.set_major_formatter(NullFormatter())
    ax.yaxis.set_major_formatter(NullFormatter())
    ax.axis("tight")

# Another example using s-curve
X, color = datasets.make_s_curve(n_samples, random_state=0)

ax = subplots[1][0]
ax.scatter(X[:, 0], X[:, 2], c=color)
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())

for i, perplexity in enumerate(perplexities):
    ax = subplots[1][i + 1]

    t0 = time()
    tsne = manifold.TSNE(
        n_components=n_components,
        init="random",
        random_state=0,
        perplexity=perplexity,
        learning_rate="auto",
        max_iter=300,
    )
    Y = tsne.fit_transform(X)
    t1 = time()
    print("S-curve, perplexity=%d in %.2g sec" % (perplexity, t1 - t0))

    ax.set_title("Perplexity=%d" % perplexity)
    ax.scatter(Y[:, 0], Y[:, 1], c=color)
    ax.xaxis.set_major_formatter(NullFormatter())
    ax.yaxis.set_major_formatter(NullFormatter())
    ax.axis("tight")


# Another example using a 2D uniform grid
x = np.linspace(0, 1, int(np.sqrt(n_samples)))
xx, yy = np.meshgrid(x, x)
X = np.hstack(
    [
        xx.ravel().reshape(-1, 1),
        yy.ravel().reshape(-1, 1),
    ]
)
color = xx.ravel()
ax = subplots[2][0]
ax.scatter(X[:, 0], X[:, 1], c=color)
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())

for i, perplexity in enumerate(perplexities):
    ax = subplots[2][i + 1]

    t0 = time()
    tsne = manifold.TSNE(
        n_components=n_components,
        init="random",
        random_state=0,
        perplexity=perplexity,
        max_iter=400,
    )
    Y = tsne.fit_transform(X)
    t1 = time()
    print("uniform grid, perplexity=%d in %.2g sec" % (perplexity, t1 - t0))

    ax.set_title("Perplexity=%d" % perplexity)
    ax.scatter(Y[:, 0], Y[:, 1], c=color)
    ax.xaxis.set_major_formatter(NullFormatter())
    ax.yaxis.set_major_formatter(NullFormatter())
    ax.axis("tight")


plt.show()

Verwandte Beispiele

Manifold Learning Methoden auf einer abgetrennten Sphäre

Manifold Learning Methoden auf einer abgetrennten Sphäre

Annähernde nächste Nachbarn in TSNE

Annähernde nächste Nachbarn in TSNE

Vergleich von Manifold Learning Methoden

Vergleich von Manifold Learning Methoden

Swiss Roll und Swiss-Hole Reduktion

Swiss Roll und Swiss-Hole Reduktion