Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Nachbearbeitung des Entscheidungsschwellenwerts für kostenorientiertes Lernen#
Sobald ein Klassifikator trainiert ist, gibt die Ausgabe der Methode predict Klassenvorhersagen aus, die einer Schwellenwertbildung entweder der Ausgabe von decision_function oder von predict_proba entsprechen. Für einen binären Klassifikator ist der Standard-Schwellenwert eine Schätzung der Posterior-Wahrscheinlichkeit von 0,5 oder ein Entscheidungswert von 0,0.
Diese Standardstrategie ist jedoch für die jeweilige Aufgabe höchstwahrscheinlich nicht optimal. Hier verwenden wir den "Statlog" German Credit Datensatz [1], um einen Anwendungsfall zu veranschaulichen. In diesem Datensatz besteht die Aufgabe darin, vorherzusagen, ob eine Person eine "gute" oder "schlechte" Bonität hat. Darüber hinaus wird eine Kostenmatrix bereitgestellt, die die Kosten für Fehlklassifizierungen angibt. Insbesondere ist die Fehlklassifizierung eines "schlechten" Kredits als "gut" im Durchschnitt fünfmal teurer als die Fehlklassifizierung eines "guten" Kredits als "schlecht".
Wir verwenden TunedThresholdClassifierCV, um den Grenzwert der Entscheidungfunktion auszuwählen, der die angegebene geschäftliche Kosten minimiert.
Im zweiten Teil des Beispiels erweitern wir diesen Ansatz weiter, indem wir das Problem der Betrugserkennung bei Kreditkartentransaktionen betrachten: In diesem Fall hängt die geschäftliche Kennzahl vom Betrag jeder einzelnen Transaktion ab.
Referenzen
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Kostenorientiertes Lernen mit konstanten Gewinnen und Kosten#
In diesem ersten Abschnitt veranschaulichen wir die Verwendung von TunedThresholdClassifierCV in einem Szenario des kostenorientierten Lernens, wenn die Gewinne und Kosten, die mit jedem Eintrag der Konfusionsmatrix verbunden sind, konstant sind. Wir verwenden das Problem, das in [2] mit dem "Statlog" German Credit Datensatz [1] vorgestellt wurde.
"Statlog" German Credit Datensatz#
Wir laden den German Credit Datensatz von OpenML.
import sklearn
from sklearn.datasets import fetch_openml
sklearn.set_config(transform_output="pandas")
german_credit = fetch_openml(data_id=31, as_frame=True, parser="pandas")
X, y = german_credit.data, german_credit.target
Wir prüfen die verfügbaren Merkmalstypen in X.
X.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 20 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 checking_status 1000 non-null category
1 duration 1000 non-null int64
2 credit_history 1000 non-null category
3 purpose 1000 non-null category
4 credit_amount 1000 non-null int64
5 savings_status 1000 non-null category
6 employment 1000 non-null category
7 installment_commitment 1000 non-null int64
8 personal_status 1000 non-null category
9 other_parties 1000 non-null category
10 residence_since 1000 non-null int64
11 property_magnitude 1000 non-null category
12 age 1000 non-null int64
13 other_payment_plans 1000 non-null category
14 housing 1000 non-null category
15 existing_credits 1000 non-null int64
16 job 1000 non-null category
17 num_dependents 1000 non-null int64
18 own_telephone 1000 non-null category
19 foreign_worker 1000 non-null category
dtypes: category(13), int64(7)
memory usage: 69.9 KB
Viele Merkmale sind kategorial und typischerweise als Zeichenketten kodiert. Wir müssen diese Kategorien kodieren, wenn wir unser Vorhersagemodell entwickeln. Lassen Sie uns die Zielvariablen überprüfen.
y.value_counts()
class
good 700
bad 300
Name: count, dtype: int64
Eine weitere Beobachtung ist, dass der Datensatz unausgeglichen ist. Wir müssen bei der Bewertung unseres Vorhersagemodells vorsichtig sein und eine Familie von Metriken verwenden, die für dieses Szenario angepasst sind.
Darüber hinaus stellen wir fest, dass die Zielvariable als Zeichenkette kodiert ist. Einige Metriken (z. B. Präzision und Recall) erfordern die Angabe des interessierenden Labels, auch "positives Label" genannt. Hier definieren wir, dass unser Ziel darin besteht, vorherzusagen, ob eine Stichprobe einen "schlechten" oder keinen "schlechten" Kredit hat.
pos_label, neg_label = "bad", "good"
Um unsere Analyse durchzuführen, teilen wir unseren Datensatz mit einer einzigen geschichteten Aufteilung auf.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)
Wir sind bereit, unser Vorhersagemodell und die zugehörige Bewertungsstrategie zu entwerfen.
Bewertungsmetriken#
In diesem Abschnitt definieren wir eine Reihe von Metriken, die wir später verwenden. Um den Effekt der Anpassung des Grenzwerts zu sehen, bewerten wir das Vorhersagemodell anhand der Receiver Operating Characteristic (ROC)-Kurve und der Precision-Recall-Kurve. Die auf diesen Diagrammen dargestellten Werte sind daher die True Positive Rate (TPR), auch bekannt als Recall oder Sensitivität, und die False Positive Rate (FPR), auch bekannt als Spezifität, für die ROC-Kurve sowie Präzision und Recall für die Precision-Recall-Kurve.
Von diesen vier Metriken stellt scikit-learn keinen Score für die FPR zur Verfügung. Wir müssen daher eine kleine benutzerdefinierte Funktion definieren, um diese zu berechnen.
from sklearn.metrics import confusion_matrix
def fpr_score(y, y_pred, neg_label, pos_label):
cm = confusion_matrix(y, y_pred, labels=[neg_label, pos_label])
tn, fp, _, _ = cm.ravel()
tnr = tn / (tn + fp)
return 1 - tnr
Wie bereits erwähnt, ist das "positive Label" nicht als Wert "1" definiert, und das Aufrufen einiger Metriken mit diesem nicht standardmäßigen Wert führt zu einem Fehler. Wir müssen den Metriken die Angabe des "positiven Labels" übergeben.
Wir definieren daher einen scikit-learn-Score mit make_scorer, bei dem die Informationen übergeben werden. Wir speichern alle benutzerdefinierten Scores in einem Wörterbuch. Um sie zu verwenden, müssen wir das trainierte Modell, die Daten und die Zielvariable übergeben, auf der wir das Vorhersagemodell bewerten möchten.
from sklearn.metrics import make_scorer, precision_score, recall_score
tpr_score = recall_score # TPR and recall are the same metric
scoring = {
"precision": make_scorer(precision_score, pos_label=pos_label),
"recall": make_scorer(recall_score, pos_label=pos_label),
"fpr": make_scorer(fpr_score, neg_label=neg_label, pos_label=pos_label),
"tpr": make_scorer(tpr_score, pos_label=pos_label),
}
Darüber hinaus definiert die Originalforschung [1] eine benutzerdefinierte Geschäftsmetrik. Wir bezeichnen eine "Geschäftsmetrik" als jede Metrikfunktion, die quantifizieren soll, wie sich die Vorhersagen (korrekt oder falsch) auf den Geschäftswert der Bereitstellung eines bestimmten Machine-Learning-Modells in einem spezifischen Anwendungskontext auswirken könnten. Für unsere Kreditvorhersageaufgabe stellen die Autoren eine benutzerdefinierte Kostenmatrix zur Verfügung, die besagt, dass die Klassifizierung eines "schlechten" Kredits als "gut" 5-mal teurer ist als das Gegenteil: Für das Finanzinstitut ist es weniger kostspielig, einem potenziellen Kunden, der nicht ausfällt, keinen Kredit zu gewähren (und somit einen guten Kunden zu verpassen, der ansonsten sowohl den Kredit zurückgezahlt als auch Zinsen gezahlt hätte), als einem Kunden, der ausfällt, einen Kredit zu gewähren.
Wir definieren eine Python-Funktion, die die Konfusionsmatrix gewichtet und die Gesamtkosten zurückgibt. Die Zeilen der Konfusionsmatrix enthalten die Zählungen der beobachteten Klassen, während die Spalten die Zählungen der vorhergesagten Klassen enthalten. Denken Sie daran, dass wir hier "schlecht" als positive Klasse betrachten (zweite Zeile und Spalte). Scikit-learn-Modellauswahl-Tools erwarten, dass wir die Konvention einhalten, dass "höher" "besser" bedeutet. Daher weist die folgende Gewinnmatrix den beiden Arten von Vorhersagefehlern negative Gewinne (Kosten) zu:
ein Gewinn von
-1für jeden falsch positiven Fall ("guter" Kredit als "schlecht" eingestuft),ein Gewinn von
-5für jeden falsch negativen Fall ("schlechter" Kredit als "gut" eingestuft),ein Gewinn von
0für richtig positive und richtig negative Fälle.
Beachten Sie, dass wir theoretisch, da unser Modell kalibriert ist und unser Datensatz repräsentativ und ausreichend groß ist, den Schwellenwert nicht anpassen müssen, sondern ihn sicher auf 1/5 des Kostenverhältnisses setzen können, wie in Gleichung (2) in Elkans Arbeit angegeben [2].
import numpy as np
def credit_gain_score(y, y_pred, neg_label, pos_label):
cm = confusion_matrix(y, y_pred, labels=[neg_label, pos_label])
gain_matrix = np.array(
[
[0, -1], # -1 gain for false positives
[-5, 0], # -5 gain for false negatives
]
)
return np.sum(cm * gain_matrix)
scoring["credit_gain"] = make_scorer(
credit_gain_score, neg_label=neg_label, pos_label=pos_label
)
Vanilla-Vorhersagemodell#
Wir verwenden HistGradientBoostingClassifier als Vorhersagemodell, das kategoriale Merkmale und fehlende Werte nativ verarbeitet.
from sklearn.ensemble import HistGradientBoostingClassifier
model = HistGradientBoostingClassifier(
categorical_features="from_dtype", random_state=0
).fit(X_train, y_train)
model
Wir bewerten die Leistung unseres Vorhersagemodells mithilfe der ROC- und Precision-Recall-Kurven.
import matplotlib.pyplot as plt
from sklearn.metrics import PrecisionRecallDisplay, RocCurveDisplay
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))
PrecisionRecallDisplay.from_estimator(
model, X_test, y_test, pos_label=pos_label, ax=axs[0], name="GBDT"
)
axs[0].plot(
scoring["recall"](model, X_test, y_test),
scoring["precision"](model, X_test, y_test),
marker="o",
markersize=10,
color="tab:blue",
label="Default cut-off point at a probability of 0.5",
)
axs[0].set_title("Precision-Recall curve")
axs[0].legend()
RocCurveDisplay.from_estimator(
model,
X_test,
y_test,
pos_label=pos_label,
ax=axs[1],
name="GBDT",
plot_chance_level=True,
)
axs[1].plot(
scoring["fpr"](model, X_test, y_test),
scoring["tpr"](model, X_test, y_test),
marker="o",
markersize=10,
color="tab:blue",
label="Default cut-off point at a probability of 0.5",
)
axs[1].set_title("ROC curve")
axs[1].legend()
_ = fig.suptitle("Evaluation of the vanilla GBDT model")

Wir erinnern uns, dass diese Kurven Einblicke in die statistische Leistung des Vorhersagemodells für verschiedene Schwellenwerte geben. Für die Precision-Recall-Kurve sind die berichteten Metriken die Präzision und der Recall, und für die ROC-Kurve sind die berichteten Metriken die TPR (gleich dem Recall) und die FPR.
Hier entsprechen die verschiedenen Schwellenwerte unterschiedlichen Ebenen der Posterior-Wahrscheinlichkeitsschätzungen im Bereich von 0 bis 1. Standardmäßig verwendet model.predict einen Schwellenwert von 0,5 Wahrscheinlichkeitsschätzung. Die Metriken für einen solchen Schwellenwert werden mit dem blauen Punkt auf den Kurven dargestellt: Es entspricht der statistischen Leistung des Modells bei Verwendung von model.predict.
Wir erinnern uns jedoch, dass das ursprüngliche Ziel darin bestand, die Kosten zu minimieren (oder den Gewinn zu maximieren), wie in der Geschäftsmetrik definiert. Wir können den Wert der Geschäftsmetrik berechnen
print(f"Business defined metric: {scoring['credit_gain'](model, X_test, y_test)}")
Business defined metric: -232
An diesem Punkt wissen wir nicht, ob ein anderer Schwellenwert zu einem größeren Gewinn führen kann. Um den optimalen zu finden, müssen wir den Kosten-Gewinn mithilfe der Geschäftsmetrik für alle möglichen Schwellenwerte berechnen und den besten auswählen. Diese Strategie kann von Hand etwas mühsam zu implementieren sein, aber die Klasse TunedThresholdClassifierCV ist hier, um uns zu helfen. Sie berechnet automatisch die Kosten-Gewinne für alle möglichen Schwellenwerte und optimiert für das `scoring`.
Anpassung des Entscheidungsschwellenwerts#
Wir verwenden TunedThresholdClassifierCV, um den Entscheidungsschwellenwert anzupassen. Wir müssen die zu optimierende Geschäftsmetrik sowie das positive Label angeben. Intern wird der optimale Entscheidungsschwellenwert so gewählt, dass er die Geschäftsmetrik über Kreuzvalidierung maximiert. Standardmäßig wird eine 5-fache geschichtete Kreuzvalidierung verwendet.
from sklearn.model_selection import TunedThresholdClassifierCV
tuned_model = TunedThresholdClassifierCV(
estimator=model,
scoring=scoring["credit_gain"],
store_cv_results=True, # necessary to inspect all results
)
tuned_model.fit(X_train, y_train)
print(f"{tuned_model.best_threshold_=:0.2f}")
tuned_model.best_threshold_=0.02
Wir plotten die ROC- und Precision-Recall-Kurven für das Vanilla-Modell und das angepasste Modell. Außerdem plotten wir die Entscheidungsschwellenwerte, die jedes Modell verwenden würde. Da wir später denselben Code wiederverwenden, definieren wir eine Funktion, die die Plots generiert.
def plot_roc_pr_curves(vanilla_model, tuned_model, *, title):
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(21, 6))
linestyles = ("dashed", "dotted")
markerstyles = ("o", ">")
colors = ("tab:blue", "tab:orange")
names = ("Vanilla GBDT", "Tuned GBDT")
for idx, (est, linestyle, marker, color, name) in enumerate(
zip((vanilla_model, tuned_model), linestyles, markerstyles, colors, names)
):
decision_threshold = getattr(est, "best_threshold_", 0.5)
PrecisionRecallDisplay.from_estimator(
est,
X_test,
y_test,
pos_label=pos_label,
linestyle=linestyle,
color=color,
ax=axs[0],
name=name,
)
axs[0].plot(
scoring["recall"](est, X_test, y_test),
scoring["precision"](est, X_test, y_test),
marker,
markersize=10,
color=color,
label=f"Cut-off point at probability of {decision_threshold:.2f}",
)
RocCurveDisplay.from_estimator(
est,
X_test,
y_test,
pos_label=pos_label,
curve_kwargs=dict(linestyle=linestyle, color=color),
ax=axs[1],
name=name,
plot_chance_level=idx == 1,
)
axs[1].plot(
scoring["fpr"](est, X_test, y_test),
scoring["tpr"](est, X_test, y_test),
marker,
markersize=10,
color=color,
label=f"Cut-off point at probability of {decision_threshold:.2f}",
)
axs[0].set_title("Precision-Recall curve")
axs[0].legend()
axs[1].set_title("ROC curve")
axs[1].legend()
axs[2].plot(
tuned_model.cv_results_["thresholds"],
tuned_model.cv_results_["scores"],
color="tab:orange",
)
axs[2].plot(
tuned_model.best_threshold_,
tuned_model.best_score_,
"o",
markersize=10,
color="tab:orange",
label="Optimal cut-off point for the business metric",
)
axs[2].legend()
axs[2].set_xlabel("Decision threshold (probability)")
axs[2].set_ylabel("Objective score (using cost-matrix)")
axs[2].set_title("Objective score as a function of the decision threshold")
fig.suptitle(title)
title = "Comparison of the cut-off point for the vanilla and tuned GBDT model"
plot_roc_pr_curves(model, tuned_model, title=title)

Die erste Bemerkung ist, dass beide Klassifikatoren exakt dieselben ROC- und Precision-Recall-Kurven haben. Dies ist zu erwarten, da der Klassifikator standardmäßig auf denselben Trainingsdaten trainiert wird. In einem späteren Abschnitt werden wir die verfügbaren Optionen bezüglich Modellretraining und Kreuzvalidierung ausführlicher diskutieren.
Die zweite Bemerkung ist, dass die Entscheidungsschwellenwerte des Vanilla- und des angepassten Modells unterschiedlich sind. Um zu verstehen, warum das angepasste Modell diesen Entscheidungsschwellenwert gewählt hat, können wir uns das Diagramm auf der rechten Seite ansehen, das den Zielfunktionswert plottet, der exakt derselbe wie unsere Geschäftsmetrik ist. Wir sehen, dass der optimale Schwellenwert dem Maximum des Zielfunktionswerts entspricht. Dieses Maximum wird für einen Entscheidungsschwellenwert erreicht, der viel niedriger als 0,5 ist: Das angepasste Modell erzielt einen viel höheren Recall auf Kosten einer signifikant niedrigeren Präzision: Das angepasste Modell ist viel eifriger, das "schlechte" Klassenlabel einem größeren Anteil von Personen zuzuordnen.
Wir können nun prüfen, ob die Wahl dieses Entscheidungsschwellenwerts zu einem besseren Score auf dem Testdatensatz führt
print(f"Business defined metric: {scoring['credit_gain'](tuned_model, X_test, y_test)}")
Business defined metric: -134
Wir beobachten, dass die Anpassung des Entscheidungsschwellenwerts unsere geschäftlichen Gewinne fast verdoppelt.
Überlegungen zu Modellretraining und Kreuzvalidierung#
Im obigen Experiment haben wir die Standardeinstellungen von TunedThresholdClassifierCV verwendet. Insbesondere wird der Entscheidungsschwellenwert mithilfe einer 5-fachen geschichteten Kreuzvalidierung angepasst. Außerdem wird das zugrunde liegende Vorhersagemodell nach Auswahl des Entscheidungsschwellenwerts auf den gesamten Trainingsdaten neu trainiert.
Diese beiden Strategien können durch Angabe der Parameter refit und cv geändert werden. Man könnte beispielsweise einen trainierten estimator angeben und cv="prefit" setzen, in diesem Fall wird der Entscheidungsschwellenwert auf dem gesamten zum Zeitpunkt des Trainings bereitgestellten Datensatz ermittelt. Außerdem wird der zugrunde liegende Klassifikator durch Setzen von refit=False nicht neu trainiert. Hier können wir versuchen, ein solches Experiment durchzuführen.
model.fit(X_train, y_train)
tuned_model.set_params(cv="prefit", refit=False).fit(X_train, y_train)
print(f"{tuned_model.best_threshold_=:0.2f}")
tuned_model.best_threshold_=0.28
Dann bewerten wir unser Modell mit demselben Ansatz wie zuvor
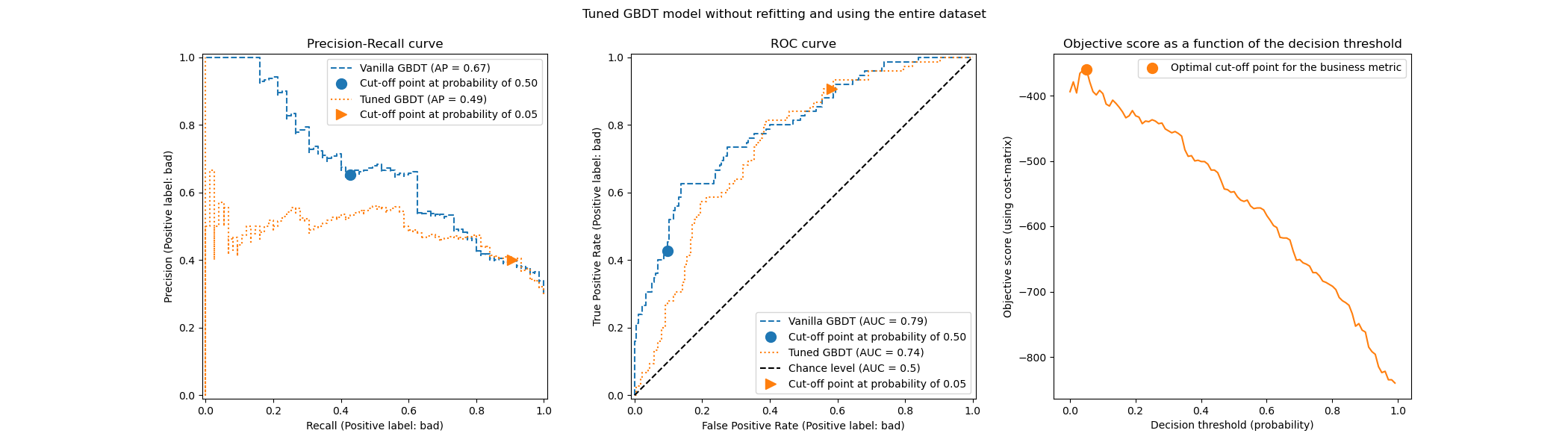
title = "Tuned GBDT model without refitting and using the entire dataset"
plot_roc_pr_curves(model, tuned_model, title=title)

Wir stellen fest, dass der optimale Entscheidungsschwellenwert von dem im vorherigen Experiment gefundenen abweicht. Wenn wir uns das Diagramm auf der rechten Seite ansehen, stellen wir fest, dass der geschäftliche Gewinn ein breites Plateau mit einem nahezu optimalen Gewinn von 0 über einen großen Bereich von Entscheidungsschwellenwerten aufweist. Dieses Verhalten ist symptomatisch für Overfitting. Da wir die Kreuzvalidierung deaktiviert haben, haben wir den Entscheidungsschwellenwert auf demselben Satz wie das trainierte Modell angepasst, und das ist der Grund für das beobachtete Overfitting.
Diese Option sollte daher mit Vorsicht verwendet werden. Man muss sicherstellen, dass die zum Trainieren des `estimator` an TunedThresholdClassifierCV bereitgestellten Daten nicht dieselben sind wie die Daten, die zum Trainieren des zugrunde liegenden Klassifikators verwendet wurden. Dies kann manchmal vorkommen, wenn die Idee darin besteht, das Vorhersagemodell einfach auf einem völlig neuen Validierungsdatensatz zu optimieren, ohne ein kostspieliges vollständiges Retraining.
Wenn die Kreuzvalidierung zu kostspielig ist, ist eine mögliche Alternative die Verwendung einer einzigen Train-Test-Aufteilung, indem eine Gleitkommazahl im Bereich [0, 1] für den Parameter cv angegeben wird. Dies teilt die Daten in einen Trainings- und einen Testsatz auf. Lassen Sie uns diese Option untersuchen
tuned_model.set_params(cv=0.75).fit(X_train, y_train)
title = "Tuned GBDT model without refitting and using the entire dataset"
plot_roc_pr_curves(model, tuned_model, title=title)
In Bezug auf den Entscheidungsschwellenwert beobachten wir, dass das Optimum dem Fall der mehrfachen wiederholten Kreuzvalidierung ähnelt. Seien Sie sich jedoch bewusst, dass ein einzelner Split die Variabilität des Fit/Predict-Prozesses nicht berücksichtigt und wir daher nicht wissen können, ob eine Varianz im Entscheidungsschwellenwert vorhanden ist. Die wiederholte Kreuzvalidierung mittelt diesen Effekt aus.
Eine weitere Beobachtung betrifft die ROC- und Precision-Recall-Kurven des angepassten Modells. Wie erwartet unterscheiden sich diese Kurven von denen des Vanilla-Modells, da wir den zugrunde liegenden Klassifikator auf einer Teilmenge der während des Trainings bereitgestellten Daten trainiert und einen Validierungsdatensatz für die Anpassung des Entscheidungsschwellenwerts reserviert haben.
Kostenorientiertes Lernen, wenn Gewinne und Kosten nicht konstant sind#
Wie in [2] angegeben, sind Gewinne und Kosten in realen Problemen im Allgemeinen nicht konstant. In diesem Abschnitt verwenden wir ein ähnliches Beispiel wie in [2] für das Problem der Erkennung von Betrug bei Kreditkartentransaktionsaufzeichnungen.
Der Kreditkartendatensatz#
credit_card = fetch_openml(data_id=1597, as_frame=True, parser="pandas")
credit_card.frame.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 284807 entries, 0 to 284806
Data columns (total 30 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V1 284807 non-null float64
1 V2 284807 non-null float64
2 V3 284807 non-null float64
3 V4 284807 non-null float64
4 V5 284807 non-null float64
5 V6 284807 non-null float64
6 V7 284807 non-null float64
7 V8 284807 non-null float64
8 V9 284807 non-null float64
9 V10 284807 non-null float64
10 V11 284807 non-null float64
11 V12 284807 non-null float64
12 V13 284807 non-null float64
13 V14 284807 non-null float64
14 V15 284807 non-null float64
15 V16 284807 non-null float64
16 V17 284807 non-null float64
17 V18 284807 non-null float64
18 V19 284807 non-null float64
19 V20 284807 non-null float64
20 V21 284807 non-null float64
21 V22 284807 non-null float64
22 V23 284807 non-null float64
23 V24 284807 non-null float64
24 V25 284807 non-null float64
25 V26 284807 non-null float64
26 V27 284807 non-null float64
27 V28 284807 non-null float64
28 Amount 284807 non-null float64
29 Class 284807 non-null category
dtypes: category(1), float64(29)
memory usage: 63.3 MB
Der Datensatz enthält Informationen über Kreditkarteneinträge, von denen einige betrügerisch und andere legitim sind. Das Ziel ist daher, vorherzusagen, ob ein Kreditkarteneintrag betrügerisch ist oder nicht.
columns_to_drop = ["Class"]
data = credit_card.frame.drop(columns=columns_to_drop)
target = credit_card.frame["Class"].astype(int)
Zuerst überprüfen wir die Klassenverteilung der Datensätze.
target.value_counts(normalize=True)
Class
0 0.998273
1 0.001727
Name: proportion, dtype: float64
Der Datensatz ist stark unausgeglichen, wobei betrügerische Transaktionen nur 0,17 % der Daten ausmachen. Da wir daran interessiert sind, ein Machine-Learning-Modell zu trainieren, sollten wir auch sicherstellen, dass wir genügend Stichproben in der Minderheitsklasse haben, um das Modell zu trainieren.
target.value_counts()
Class
0 284315
1 492
Name: count, dtype: int64
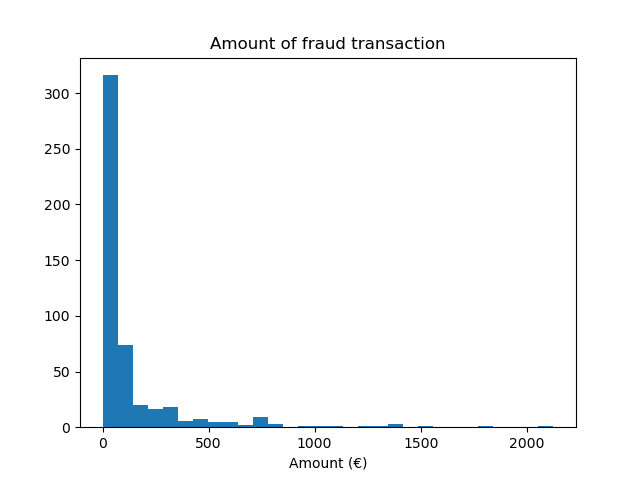
Wir stellen fest, dass wir ungefähr 500 Stichproben haben, was am unteren Ende der Anzahl der für das Training eines Machine-Learning-Modells erforderlichen Stichproben liegt. Zusätzlich zur Zielverteilung überprüfen wir die Verteilung des Betrags der betrügerischen Transaktionen.
fraud = target == 1
amount_fraud = data["Amount"][fraud]
_, ax = plt.subplots()
ax.hist(amount_fraud, bins=30)
ax.set_title("Amount of fraud transaction")
_ = ax.set_xlabel("Amount (€)")
Das Problem mit einer Geschäftsmetrik lösen#
Nun erstellen wir die Geschäftsmetrik, die vom Betrag jeder Transaktion abhängt. Wir definieren die Kostenmatrix ähnlich wie in [2]. Die Annahme einer legitimen Transaktion bringt einen Gewinn von 2 % des Transaktionsbetrags. Die Annahme einer betrügerischen Transaktion führt jedoch zu einem Verlust des Transaktionsbetrags. Wie in [2] angegeben, sind die Gewinne und Verluste im Zusammenhang mit Ablehnungen (von betrügerischen und legitimen Transaktionen) nicht einfach zu definieren. Hier definieren wir, dass die Ablehnung einer legitimen Transaktion mit einem Verlust von 5 € geschätzt wird, während die Ablehnung einer betrügerischen Transaktion mit einem Gewinn von 50 € geschätzt wird. Daher definieren wir die folgende Funktion, um den Gesamtgewinn einer gegebenen Entscheidung zu berechnen
def business_metric(y_true, y_pred, amount):
mask_true_positive = (y_true == 1) & (y_pred == 1)
mask_true_negative = (y_true == 0) & (y_pred == 0)
mask_false_positive = (y_true == 0) & (y_pred == 1)
mask_false_negative = (y_true == 1) & (y_pred == 0)
fraudulent_refuse = mask_true_positive.sum() * 50
fraudulent_accept = -amount[mask_false_negative].sum()
legitimate_refuse = mask_false_positive.sum() * -5
legitimate_accept = (amount[mask_true_negative] * 0.02).sum()
return fraudulent_refuse + fraudulent_accept + legitimate_refuse + legitimate_accept
Aus dieser Geschäftsmetrik erstellen wir einen scikit-learn-Score, der, gegeben einen trainierten Klassifikator und einen Testdatensatz, die Geschäftsmetrik berechnet. In diesem Zusammenhang verwenden wir die Fabrik make_scorer. Die Variable amount ist ein zusätzliches Metadatum, das an den Score übergeben werden muss, und wir müssen Metadaten-Routing verwenden, um diese Informationen zu berücksichtigen.
sklearn.set_config(enable_metadata_routing=True)
business_scorer = make_scorer(business_metric).set_score_request(amount=True)
An diesem Punkt stellen wir fest, dass der Betrag der Transaktion zweimal verwendet wird: einmal als Merkmal zum Trainieren unseres Vorhersagemodells und einmal als Metadatum zur Berechnung der Geschäftsmetrik und damit der statistischen Leistung unseres Modells. Wenn es als Merkmal verwendet wird, benötigen wir nur eine Spalte in data, die den Betrag jeder Transaktion enthält. Um diese Informationen als Metadaten zu verwenden, benötigen wir eine externe Variable, die wir an den Score oder das Modell übergeben können, das diese Metadaten intern an den Score weiterleitet. Lassen Sie uns also diese Variable erstellen.
amount = credit_card.frame["Amount"].to_numpy()
from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test, amount_train, amount_test = (
train_test_split(
data, target, amount, stratify=target, test_size=0.5, random_state=42
)
)
Wir bewerten zunächst einige Basisrichtlinien als Referenz. Erinnern Sie sich, dass Klasse "0" die legitime Klasse und Klasse "1" die betrügerische Klasse ist.
from sklearn.dummy import DummyClassifier
always_accept_policy = DummyClassifier(strategy="constant", constant=0)
always_accept_policy.fit(data_train, target_train)
benefit = business_scorer(
always_accept_policy, data_test, target_test, amount=amount_test
)
print(f"Benefit of the 'always accept' policy: {benefit:,.2f}€")
Benefit of the 'always accept' policy: 221,445.07€
Eine Richtlinie, die alle Transaktionen als legitim betrachtet, würde einen Gewinn von rund 220.000 € erzielen. Wir machen dieselbe Bewertung für einen Klassifikator, der alle Transaktionen als betrügerisch einstuft.
always_reject_policy = DummyClassifier(strategy="constant", constant=1)
always_reject_policy.fit(data_train, target_train)
benefit = business_scorer(
always_reject_policy, data_test, target_test, amount=amount_test
)
print(f"Benefit of the 'always reject' policy: {benefit:,.2f}€")
Benefit of the 'always reject' policy: -698,490.00€
Eine solche Richtlinie würde zu einem katastrophalen Verlust führen: rund 670.000 €. Dies ist zu erwarten, da die überwiegende Mehrheit der Transaktionen legitim ist und die Richtlinie diese zu einem nicht unerheblichen Kostenpunkt ablehnen würde.
Ein Vorhersagemodell, das die Entscheidungen über Akzeptanz/Ablehnung pro Transaktion anpasst, sollte es uns idealerweise ermöglichen, einen Gewinn zu erzielen, der größer ist als die 220.000 € unserer besten konstanten Basisrichtlinien.
Wir beginnen mit einem logistischen Regressionsmodell mit dem Standard-Entscheidungsschwellenwert von 0,5. Hier passen wir den Hyperparameter C der logistischen Regression mit einer geeigneten Scoring-Regel (dem Log-Loss) an, um sicherzustellen, dass die vom `predict_proba`-Methode zurückgegebenen Wahrscheinlichkeitsvorhersagen des Modells so genau wie möglich sind, unabhängig von der Wahl des Entscheidungsschwellenwerts.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
logistic_regression = make_pipeline(StandardScaler(), LogisticRegression())
param_grid = {"logisticregression__C": np.logspace(-6, 6, 13)}
model = GridSearchCV(logistic_regression, param_grid, scoring="neg_log_loss").fit(
data_train, target_train
)
model
Anpassung des Entscheidungsschwellenwerts#
Nun stellt sich die Frage: Ist unser Modell für die Art der Entscheidung, die wir treffen wollen, optimal? Bislang haben wir die Entscheidungsschwelle nicht optimiert. Wir verwenden TunedThresholdClassifierCV, um die Entscheidung anhand unseres Business-Scorers zu optimieren. Um eine verschachtelte Kreuzvalidierung zu vermeiden, verwenden wir den besten Schätzer, der während des vorherigen Grid-Search gefunden wurde.
tuned_model = TunedThresholdClassifierCV(
estimator=model.best_estimator_,
scoring=business_scorer,
thresholds=100,
n_jobs=2,
)
Da unser Business-Scorer den Betrag jeder Transaktion benötigt, müssen wir diese Information in der fit-Methode übergeben. Die TunedThresholdClassifierCV ist dafür zuständig, diese Metadaten automatisch an den zugrunde liegenden Scorer weiterzuleiten.
tuned_model.fit(data_train, target_train, amount=amount_train)
Manuelles Setzen der Entscheidungsschwelle anstelle ihrer Abstimmung#
Im vorherigen Beispiel haben wir TunedThresholdClassifierCV verwendet, um die optimale Entscheidungsschwelle zu finden. In einigen Fällen haben wir jedoch möglicherweise Vorwissen über das vorliegende Problem und sind möglicherweise bereit, die Entscheidungsschwelle manuell festzulegen.
Die Klasse FixedThresholdClassifier ermöglicht es uns, die Entscheidungsschwelle manuell festzulegen. Zum Zeitpunkt der Vorhersage verhält sie sich wie das vorherige abgestimmte Modell, aber während des Anpassungsprozesses wird keine Suche durchgeführt. Beachten Sie, dass wir hier FrozenEstimator verwenden, um das prädiktive Modell zu umschließen, um ein erneutes Anpassen zu vermeiden.
Hier verwenden wir die im vorherigen Abschnitt gefundene Entscheidungsschwelle wieder, um ein neues Modell zu erstellen und zu überprüfen, ob es die gleichen Ergebnisse liefert.
from sklearn.frozen import FrozenEstimator
from sklearn.model_selection import FixedThresholdClassifier
model_fixed_threshold = FixedThresholdClassifier(
estimator=FrozenEstimator(model), threshold=tuned_model.best_threshold_
)
business_score = business_scorer(
model_fixed_threshold, data_test, target_test, amount=amount_test
)
print(f"Benefit of logistic regression with a tuned threshold: {business_score:,.2f}€")
Benefit of logistic regression with a tuned threshold: 249,433.39€
Wir beobachten, dass wir exakt die gleichen Ergebnisse erzielt haben, der Anpassungsprozess jedoch viel schneller war, da wir keine Hyperparameter-Suche durchgeführt haben.
Schließlich kann die Schätzung der (durchschnittlichen) Geschäftsmetrik selbst unzuverlässig sein, insbesondere wenn die Anzahl der Datenpunkte in der Minderheitsklasse sehr gering ist. Jede Geschäftsmetrik, die durch Kreuzvalidierung einer Geschäftsmetrik auf historischen Daten (Offline-Evaluierung) geschätzt wird, sollte idealerweise durch A/B-Tests auf Live-Daten (Online-Evaluierung) bestätigt werden. Beachten Sie jedoch, dass A/B-Tests von Modellen außerhalb des Rahmens der scikit-learn-Bibliothek selbst liegen.
Am Ende deaktivieren wir die Konfigurationsflagge für das Metadaten-Routing.
.. GENERATED FROM PYTHON SOURCE LINES 694-695
sklearn.set_config(enable_metadata_routing=False)
Gesamtlaufzeit des Skripts: (0 Minuten 35,875 Sekunden)
Verwandte Beispiele
Post-hoc-Anpassung des Cut-off-Punkts der Entscheidungskfunktion

Benutzerdefinierte Refit-Strategie einer Gitter-Suche mit Kreuzvalidierung