Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Wahrscheinlichkeitskalibrierungskurven#
Bei der Durchführung von Klassifikationen möchte man oft nicht nur die Klassenbezeichnung vorhersagen, sondern auch die zugehörige Wahrscheinlichkeit. Diese Wahrscheinlichkeit gibt eine Art Vertrauen in die Vorhersage an. Dieses Beispiel zeigt, wie gut kalibriert die vorhergesagten Wahrscheinlichkeiten mithilfe von Kalibrierungskurven, auch Zuverlässigkeitsdiagramme genannt, visualisiert werden können. Auch die Kalibrierung eines unkalibrierten Klassifikators wird demonstriert.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Datensatz#
Wir verwenden einen synthetischen binären Klassifikationsdatensatz mit 100.000 Samples und 20 Merkmalen. Von den 20 Merkmalen sind nur 2 informativ, 10 sind redundant (zufällige Kombinationen der informativen Merkmale) und die restlichen 8 sind uninformativ (zufällige Zahlen). Von den 100.000 Samples werden 1.000 zum Anpassen des Modells und der Rest zum Testen verwendet.
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
X, y = make_classification(
n_samples=100_000, n_features=20, n_informative=2, n_redundant=10, random_state=42
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.99, random_state=42
)
Kalibrierungskurven#
Gaußscher Naive Bayes#
Zuerst vergleichen wir
LogisticRegression(als Basislinie verwendet, da richtig regularisierte logistische Regression dank der Verwendung des Log-Losses oft standardmäßig gut kalibriert ist)Unkalibrierter
GaussianNBGaussianNBmit isotoner und sigmoidaler Kalibrierung (siehe Benutzerhandbuch)
Die Kalibrierungskurven für alle 4 Bedingungen sind unten dargestellt, mit der durchschnittlich vorhergesagten Wahrscheinlichkeit für jedes Intervall auf der x-Achse und dem Anteil positiver Klassen in jedem Intervall auf der y-Achse.
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from sklearn.calibration import CalibratedClassifierCV, CalibrationDisplay
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
lr = LogisticRegression(C=1.0)
gnb = GaussianNB()
gnb_isotonic = CalibratedClassifierCV(gnb, cv=2, method="isotonic")
gnb_sigmoid = CalibratedClassifierCV(gnb, cv=2, method="sigmoid")
clf_list = [
(lr, "Logistic"),
(gnb, "Naive Bayes"),
(gnb_isotonic, "Naive Bayes + Isotonic"),
(gnb_sigmoid, "Naive Bayes + Sigmoid"),
]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.get_cmap("Dark2")
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (Naive Bayes)")
# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()
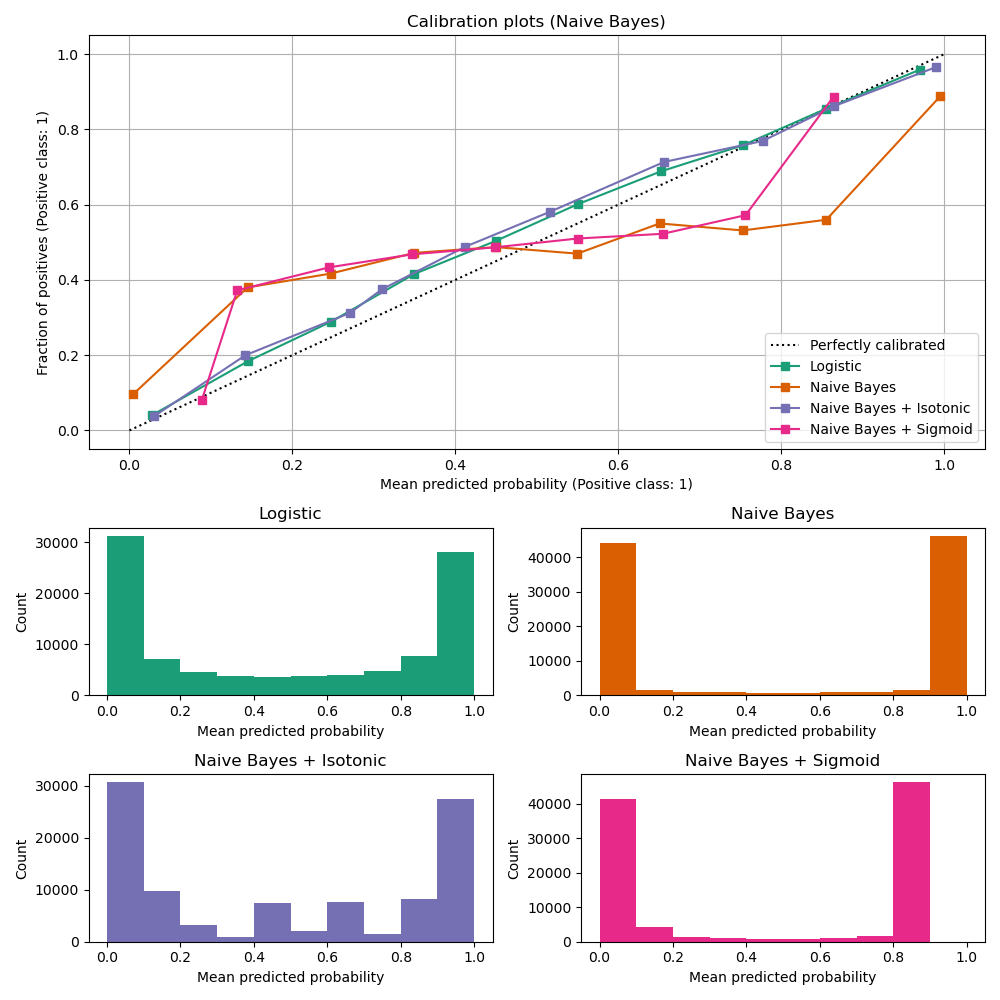
Unkalibrierter GaussianNB ist schlecht kalibriert aufgrund der redundanten Merkmale, die die Annahme der Merkmalsunabhängigkeit verletzen und zu einem übermäßig zuversichtlichen Klassifikator führen, was sich in der typischen transponierten Sigmoid-Kurve zeigt. Die Kalibrierung der Wahrscheinlichkeiten von GaussianNB mit Isotoner Regression kann dieses Problem beheben, wie aus der fast diagonalen Kalibrierungskurve ersichtlich ist. Die Sigmoid-Regression verbessert die Kalibrierung ebenfalls leicht, wenn auch nicht so stark wie die nicht-parametrische isotonische Regression. Dies kann darauf zurückgeführt werden, dass wir reichlich Kalibrierungsdaten haben, so dass die größere Flexibilität des nicht-parametrischen Modells genutzt werden kann.
Im Folgenden führen wir eine quantitative Analyse unter Berücksichtigung mehrerer Klassifikationsmetriken durch: Brier Score Loss, Log Loss, Präzision, Recall, F1-Score und ROC AUC.
from collections import defaultdict
import pandas as pd
from sklearn.metrics import (
brier_score_loss,
f1_score,
log_loss,
precision_score,
recall_score,
roc_auc_score,
)
scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
scores["Classifier"].append(name)
for metric in [brier_score_loss, log_loss, roc_auc_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_prob[:, 1]))
for metric in [precision_score, recall_score, f1_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_pred))
score_df = pd.DataFrame(scores).set_index("Classifier")
score_df.round(decimals=3)
score_df
Beachten Sie, dass die Kalibrierung zwar den Brier Score Loss (eine Metrik, die sich aus Kalibrierungs- und Verfeinerungsterm zusammensetzt) und den Log Loss verbessert, die Genauigkeitsmaße der Vorhersage (Präzision, Recall und F1-Score) jedoch nicht wesentlich verändert. Dies liegt daran, dass die Kalibrierung die vorhergesagten Wahrscheinlichkeiten an der Stelle des Entscheidungsschwellenwerts (bei x = 0,5 auf der Grafik) nicht wesentlich ändern sollte. Die Kalibrierung sollte jedoch die vorhergesagten Wahrscheinlichkeiten genauer und damit nützlicher für Entscheidungen unter Unsicherheit machen. Darüber hinaus sollte die ROC-AUC überhaupt nicht verändert werden, da die Kalibrierung eine monotone Transformation ist. Tatsächlich werden keine Rangmetriken durch Kalibrierung beeinflusst.
Linearer Support Vector Classifier#
Als Nächstes vergleichen wir
LogisticRegression(Basislinie)Unkalibrierter
LinearSVC. Da SVC standardmäßig keine Wahrscheinlichkeiten ausgibt, skalieren wir die Ausgabe der decision_function naiv auf [0, 1] durch Anwendung der Min-Max-Skalierung.LinearSVCmit isotoner und sigmoidaler Kalibrierung (siehe Benutzerhandbuch)
import numpy as np
from sklearn.svm import LinearSVC
class NaivelyCalibratedLinearSVC(LinearSVC):
"""LinearSVC with `predict_proba` method that naively scales
`decision_function` output for binary classification."""
def fit(self, X, y):
super().fit(X, y)
df = self.decision_function(X)
self.df_min_ = df.min()
self.df_max_ = df.max()
def predict_proba(self, X):
"""Min-max scale output of `decision_function` to [0, 1]."""
df = self.decision_function(X)
calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
proba_pos_class = np.clip(calibrated_df, 0, 1)
proba_neg_class = 1 - proba_pos_class
proba = np.c_[proba_neg_class, proba_pos_class]
return proba
lr = LogisticRegression(C=1.0)
svc = NaivelyCalibratedLinearSVC(max_iter=10_000)
svc_isotonic = CalibratedClassifierCV(svc, cv=2, method="isotonic")
svc_sigmoid = CalibratedClassifierCV(svc, cv=2, method="sigmoid")
clf_list = [
(lr, "Logistic"),
(svc, "SVC"),
(svc_isotonic, "SVC + Isotonic"),
(svc_sigmoid, "SVC + Sigmoid"),
]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (SVC)")
# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()
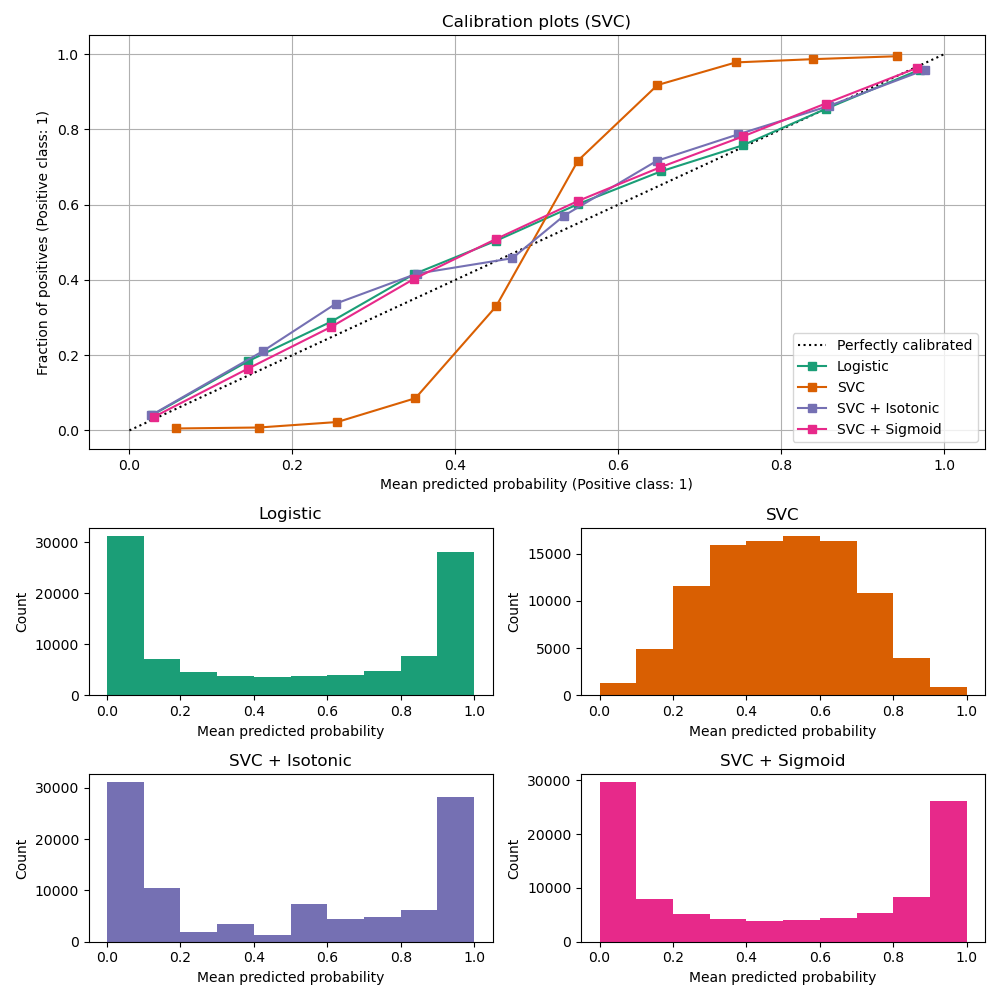
LinearSVC zeigt das entgegengesetzte Verhalten wie GaussianNB; die Kalibrierungskurve hat eine Sigmoid-Form, was typisch für einen unterzuversichtlichen Klassifikator ist. Im Fall von LinearSVC wird dies durch die Margin-Eigenschaft des Hinge-Loss verursacht, der sich auf Samples konzentriert, die nahe an der Entscheidungsgrenze liegen (Support-Vektoren). Samples, die weit von der Entscheidungsgrenze entfernt sind, beeinflussen den Hinge-Loss nicht. Es ist daher sinnvoll, dass LinearSVC nicht versucht, Samples im Bereich hoher Konfidenz zu trennen. Dies führt zu flacheren Kalibrierungskurven nahe 0 und 1 und wird empirisch mit einer Vielzahl von Datensätzen in Niculescu-Mizil & Caruana [1] gezeigt.
Beide Arten der Kalibrierung (Sigmoid und Isoton) können dieses Problem beheben und liefern ähnliche Ergebnisse.
Wie zuvor zeigen wir den Brier Score Loss, Log Loss, Präzision, Recall, F1-Score und ROC AUC.
scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
scores["Classifier"].append(name)
for metric in [brier_score_loss, log_loss, roc_auc_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_prob[:, 1]))
for metric in [precision_score, recall_score, f1_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_pred))
score_df = pd.DataFrame(scores).set_index("Classifier")
score_df.round(decimals=3)
score_df
Wie bei GaussianNB oben verbessert die Kalibrierung sowohl den Brier Score Loss als auch den Log Loss, verändert jedoch die Genauigkeitsmaße der Vorhersage (Präzision, Recall und F1-Score) nicht wesentlich.
Zusammenfassung#
Parametrische Sigmoid-Kalibrierung kann Situationen bewältigen, in denen die Kalibrierungskurve des Basisklassifikators sigmoid ist (z.B. für LinearSVC), aber nicht, wenn sie transponiert-sigmoid ist (z.B. GaussianNB). Nicht-parametrische isotonische Kalibrierung kann beide Situationen bewältigen, erfordert jedoch möglicherweise mehr Daten, um gute Ergebnisse zu erzielen.
Referenzen#
Gesamtlaufzeit des Skripts: (0 Minuten 2,376 Sekunden)
Verwandte Beispiele
Wahrscheinlichkeitskalibrierung von Klassifikatoren
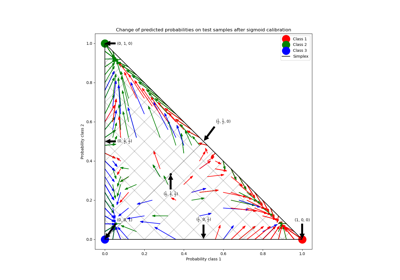
Wahrscheinlichkeitskalibrierung für 3-Klassen-Klassifikation