Lasso-Modellauswahl mittels Informationskriterien

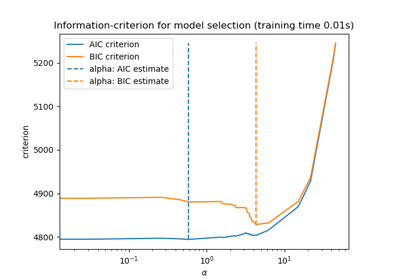
Dieses Beispiel reproduziert das Beispiel von Abb. 2 in [ZHT2007]. Ein LassoLarsIC-Schätzer wird auf einem Diabetes-Datensatz angepasst, und die Kriterien AIC und BIC werden zur Auswahl des besten Modells verwendet.

Hinweis

Es ist wichtig zu beachten, dass die Optimierung zur Ermittlung von alpha mit LassoLarsIC auf den im Trainingsdatensatz direkt berechneten AIC- oder BIC-Kriterien basiert. Dieser Ansatz unterscheidet sich vom Kreuzvalidierungsverfahren. Ein Vergleich der beiden Ansätze ist im folgenden Beispiel zu finden: Lasso-Modellauswahl: AIC-BIC / Kreuzvalidierung.

Referenzen

[ZHT2007] (1,2)

Zou, Hui, Trevor Hastie und Robert Tibshirani. „On the degrees of freedom of the lasso.“ The Annals of Statistics 35.5 (2007): 2173-2192.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Wir verwenden den Diabetes-Datensatz.

from sklearn.datasets import load_diabetes

X, y = load_diabetes(return_X_y=True, as_frame=True)
n_samples = X.shape[0]
X.head()

	Alter	geschlecht	bmi	bp	s1	s2	s3	s4	s5	s6
0	0.038076	0.050680	0.061696	0.021872	-0.044223	-0.034821	-0.043401	-0.002592	0.019907	-0.017646
1	-0.001882	-0.044642	-0.051474	-0.026328	-0.008449	-0.019163	0.074412	-0.039493	-0.068332	-0.092204
2	0.085299	0.050680	0.044451	-0.005670	-0.045599	-0.034194	-0.032356	-0.002592	0.002861	-0.025930
3	-0.089063	-0.044642	-0.011595	-0.036656	0.012191	0.024991	-0.036038	0.034309	0.022688	-0.009362
4	0.005383	-0.044642	-0.036385	0.021872	0.003935	0.015596	0.008142	-0.002592	-0.031988	-0.046641

Scikit-learn bietet einen Schätzer namens LassoLarsIC, der entweder das Akaike-Informationskriterium (AIC) oder das Bayes'sche Informationskriterium (BIC) zur Auswahl des besten Modells verwendet. Bevor wir dieses Modell anpassen, skalieren wir den Datensatz.

Im Folgenden passen wir zwei Modelle an, um die von AIC und BIC gemeldeten Werte zu vergleichen.

from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)

Um der Definition in [ZHT2007] zu entsprechen, müssen wir AIC und BIC neu skalieren. Zou et al. ignorieren nämlich einige konstante Terme im Vergleich zur ursprünglichen Definition von AIC, die sich aus der maximalen Log-Likelihood eines linearen Modells ergibt. Sie können auf den Abschnitt mathematische Details im Benutzerhandbuch verweisen.

def zou_et_al_criterion_rescaling(criterion, n_samples, noise_variance):
    """Rescale the information criterion to follow the definition of Zou et al."""
    return criterion - n_samples * np.log(2 * np.pi * noise_variance) - n_samples

import numpy as np

aic_criterion = zou_et_al_criterion_rescaling(
    lasso_lars_ic[-1].criterion_,
    n_samples,
    lasso_lars_ic[-1].noise_variance_,
)

index_alpha_path_aic = np.flatnonzero(
    lasso_lars_ic[-1].alphas_ == lasso_lars_ic[-1].alpha_
)[0]

lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)

bic_criterion = zou_et_al_criterion_rescaling(
    lasso_lars_ic[-1].criterion_,
    n_samples,
    lasso_lars_ic[-1].noise_variance_,
)

index_alpha_path_bic = np.flatnonzero(
    lasso_lars_ic[-1].alphas_ == lasso_lars_ic[-1].alpha_
)[0]

Nachdem wir die AIC- und BIC-Werte gesammelt haben, können wir auch überprüfen, ob die Minima beider Kriterien bei demselben Alpha auftreten. Dann können wir die folgende Abbildung vereinfachen.

index_alpha_path_aic == index_alpha_path_bic

np.True_

Schließlich können wir das AIC- und BIC-Kriterium sowie den darauf basierenden ausgewählten Regularisierungsparameter darstellen.

import matplotlib.pyplot as plt

plt.plot(aic_criterion, color="tab:blue", marker="o", label="AIC criterion")
plt.plot(bic_criterion, color="tab:orange", marker="o", label="BIC criterion")
plt.vlines(
    index_alpha_path_bic,
    aic_criterion.min(),
    aic_criterion.max(),
    color="black",
    linestyle="--",
    label="Selected alpha",
)
plt.legend()
plt.ylabel("Information criterion")
plt.xlabel("Lasso model sequence")
_ = plt.title("Lasso model selection via AIC and BIC")

Verwandte Beispiele

Lasso-Modellauswahl: AIC-BIC / Kreuzvalidierung

Lasso-Modellauswahl: AIC-BIC / Kreuzvalidierung

Gaußsche Mischmodell-Auswahl

Gaußsche Mischmodell-Auswahl

Frühes Stoppen von Stochastic Gradient Descent

Frühes Stoppen von Stochastic Gradient Descent

Gemeinsame Merkmalsauswahl mit Multi-Task Lasso

Gemeinsame Merkmalsauswahl mit Multi-Task Lasso