Vektor-Quantisierungs-Beispiel

Dieses Beispiel zeigt, wie man KBinsDiscretizer verwenden kann, um eine Vektorquantisierung auf einem Satz von Spielbildern, dem Waschbärgesicht, durchzuführen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Originalbild

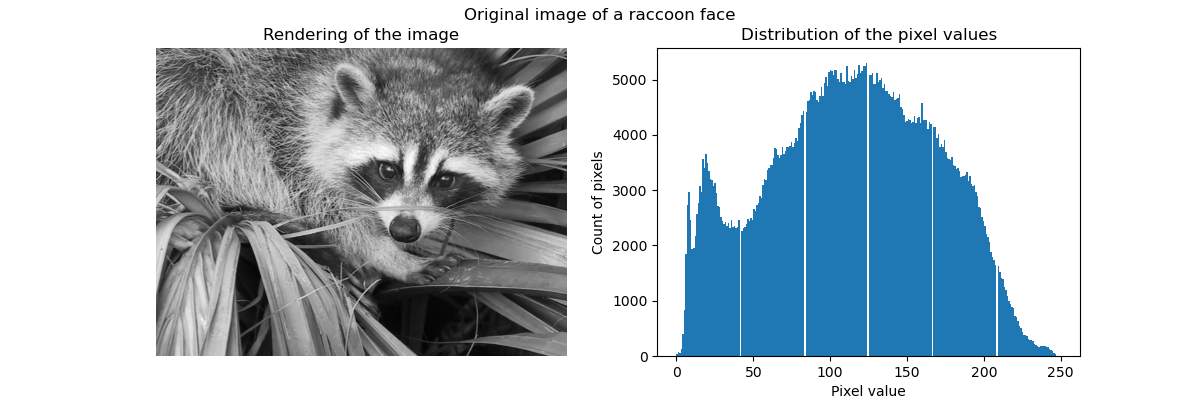
Wir laden zunächst das Waschbärgesichtsbild von SciPy. Wir überprüfen zusätzlich einige Informationen über das Bild, wie z. B. die Form und den Datentyp, der zur Speicherung des Bildes verwendet wird.

from scipy.datasets import face

raccoon_face = face(gray=True)

print(f"The dimension of the image is {raccoon_face.shape}")
print(f"The data used to encode the image is of type {raccoon_face.dtype}")
print(f"The number of bytes taken in RAM is {raccoon_face.nbytes}")

The dimension of the image is (768, 1024)
The data used to encode the image is of type uint8
The number of bytes taken in RAM is 786432

Somit ist das Bild ein 2D-Array mit 768 Pixeln Höhe und 1024 Pixeln Breite. Jeder Wert ist eine vorzeichenlose 8-Bit-Ganzzahl, was bedeutet, dass das Bild mit 8 Bits pro Pixel kodiert ist. Der Gesamtspeicherbedarf des Bildes beträgt 786 Kilobytes (1 Byte entspricht 8 Bits).

Die Verwendung einer vorzeichenlosen 8-Bit-Ganzzahl bedeutet, dass das Bild maximal mit 256 verschiedenen Graustufen kodiert ist. Wir können die Verteilung dieser Werte überprüfen.

import matplotlib.pyplot as plt

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))

ax[0].imshow(raccoon_face, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(raccoon_face.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Count of pixels")
ax[1].set_title("Distribution of the pixel values")
_ = fig.suptitle("Original image of a raccoon face")

Kompression durch Vektorquantisierung

Die Idee hinter der Kompression durch Vektorquantisierung ist, die Anzahl der Graustufen zur Darstellung eines Bildes zu reduzieren. Zum Beispiel können wir 8 Werte anstelle von 256 Werten verwenden. Daher bedeutet dies, dass wir effizient 3 Bits anstelle von 8 Bits zur Kodierung eines einzelnen Pixels verwenden und somit den Speicherbedarf um den Faktor 2,5 reduzieren könnten. Wir werden später auf diesen Speicherbedarf eingehen.

Kodierungsstrategie

Die Kompression kann mit einem KBinsDiscretizer erfolgen. Wir müssen eine Strategie wählen, um die 8 Graustufen zu definieren, die abgetastet werden sollen. Die einfachste Strategie ist, sie gleichmäßig verteilt zu definieren, was der Einstellung strategy="uniform" entspricht. Aus dem vorherigen Histogramm wissen wir, dass diese Strategie sicherlich nicht optimal ist.

from sklearn.preprocessing import KBinsDiscretizer

n_bins = 8
encoder = KBinsDiscretizer(
    n_bins=n_bins,
    encode="ordinal",
    strategy="uniform",
    random_state=0,
)
compressed_raccoon_uniform = encoder.fit_transform(raccoon_face.reshape(-1, 1)).reshape(
    raccoon_face.shape
)

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))
ax[0].imshow(compressed_raccoon_uniform, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(compressed_raccoon_uniform.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Count of pixels")
ax[1].set_title("Sub-sampled distribution of the pixel values")
_ = fig.suptitle("Raccoon face compressed using 3 bits and a uniform strategy")

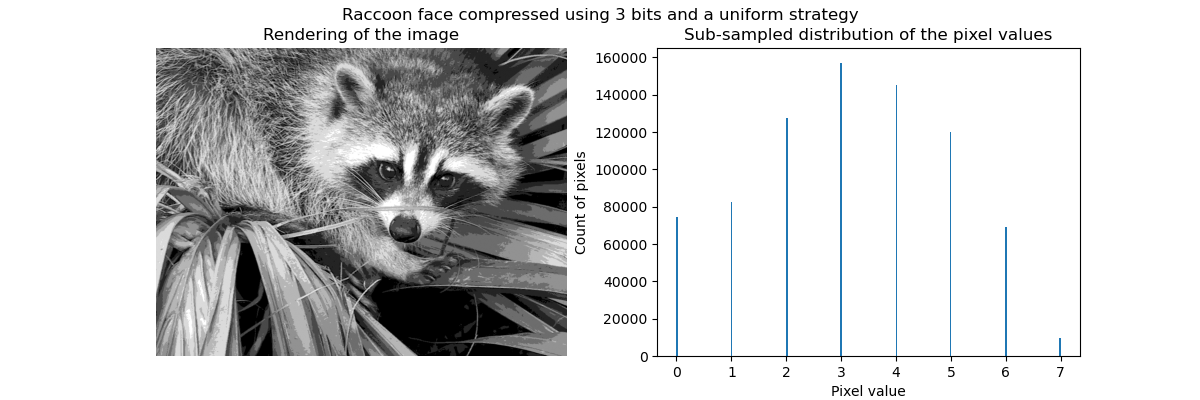
Qualitativ können wir einige kleine Bereiche erkennen, in denen wir den Effekt der Kompression sehen (z. B. Blätter in der unteren rechten Ecke). Aber im Großen und Ganzen sieht das resultierende Bild immer noch gut aus.

Wir beobachten, dass die Verteilung der Pixelwerte auf 8 verschiedene Werte abgebildet wurde. Wir können die Entsprechung zwischen diesen Werten und den ursprünglichen Pixelwerten überprüfen.

bin_edges = encoder.bin_edges_[0]
bin_center = bin_edges[:-1] + (bin_edges[1:] - bin_edges[:-1]) / 2
bin_center

array([ 15.5625,  46.6875,  77.8125, 108.9375, 140.0625, 171.1875,
       202.3125, 233.4375])

_, ax = plt.subplots()
ax.hist(raccoon_face.ravel(), bins=256)
color = "tab:orange"
for center in bin_center:
    ax.axvline(center, color=color)
    ax.text(center - 10, ax.get_ybound()[1] + 100, f"{center:.1f}", color=color)

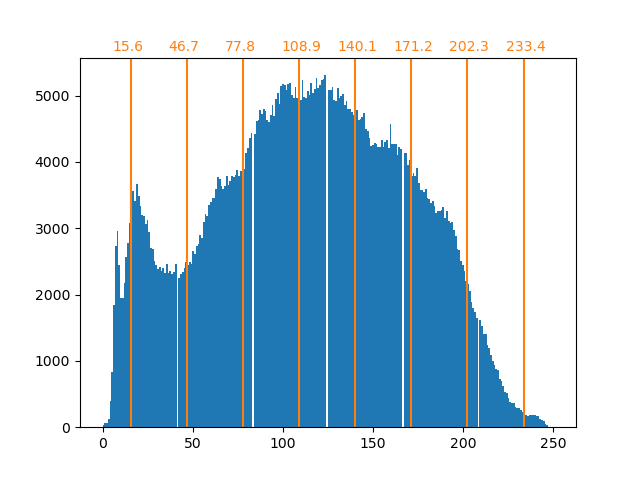
Wie bereits erwähnt, ist die gleichmäßige Abtaststrategie nicht optimal. Beachten Sie zum Beispiel, dass die Pixel, die dem Wert 7 zugeordnet sind, eher eine geringe Informationsmenge kodieren, während der zugeordnete Wert 3 eine große Anzahl von Zählungen darstellt. Wir können stattdessen eine Clustering-Strategie wie k-means verwenden, um eine optimalere Abbildung zu finden.

encoder = KBinsDiscretizer(
    n_bins=n_bins,
    encode="ordinal",
    strategy="kmeans",
    random_state=0,
)
compressed_raccoon_kmeans = encoder.fit_transform(raccoon_face.reshape(-1, 1)).reshape(
    raccoon_face.shape
)

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))
ax[0].imshow(compressed_raccoon_kmeans, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(compressed_raccoon_kmeans.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Number of pixels")
ax[1].set_title("Distribution of the pixel values")
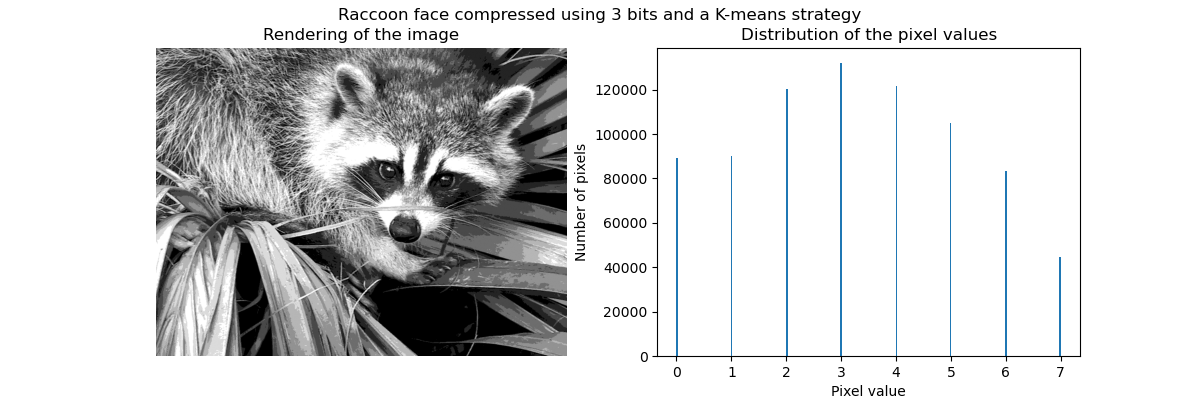
_ = fig.suptitle("Raccoon face compressed using 3 bits and a K-means strategy")

bin_edges = encoder.bin_edges_[0]
bin_center = bin_edges[:-1] + (bin_edges[1:] - bin_edges[:-1]) / 2
bin_center

array([ 18.90934343,  53.33478066,  82.59678424, 109.22385188,
       134.67876527, 159.67877978, 184.72384803, 223.17132867])

_, ax = plt.subplots()
ax.hist(raccoon_face.ravel(), bins=256)
color = "tab:orange"
for center in bin_center:
    ax.axvline(center, color=color)
    ax.text(center - 10, ax.get_ybound()[1] + 100, f"{center:.1f}", color=color)

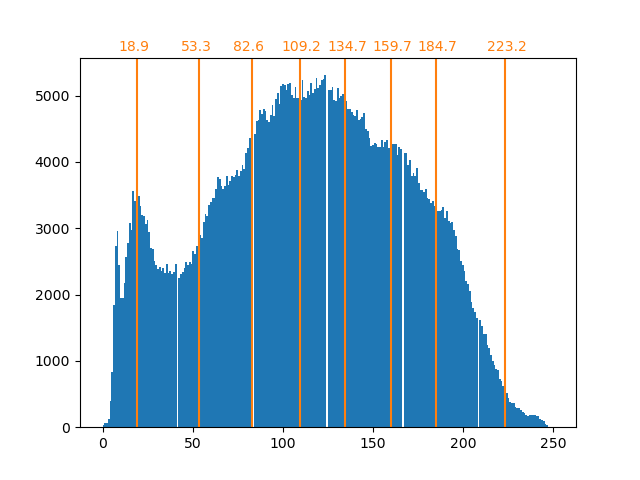
Die Zählungen in den Bins sind jetzt besser ausbalanciert und ihre Zentren sind nicht mehr gleichmäßig verteilt. Beachten Sie, dass wir die gleiche Anzahl von Pixeln pro Bin erzwingen könnten, indem wir strategy="quantile" anstelle von strategy="kmeans" verwenden.

Speicher-Fußabdruck

Wir haben zuvor angegeben, dass wir 8-mal weniger Speicher sparen sollten. Lassen Sie uns das überprüfen.

print(f"The number of bytes taken in RAM is {compressed_raccoon_kmeans.nbytes}")
print(f"Compression ratio: {compressed_raccoon_kmeans.nbytes / raccoon_face.nbytes}")

The number of bytes taken in RAM is 6291456
Compression ratio: 8.0

Es ist ziemlich überraschend zu sehen, dass unser komprimiertes Bild 8-mal mehr Speicherplatz benötigt als das Originalbild. Dies ist tatsächlich das Gegenteil dessen, was wir erwartet hatten. Der Grund liegt hauptsächlich in der Art der Daten, die zur Kodierung des Bildes verwendet werden.

print(f"Type of the compressed image: {compressed_raccoon_kmeans.dtype}")

Type of the compressed image: float64

Tatsächlich ist die Ausgabe des KBinsDiscretizer ein Array von 64-Bit-Gleitkommazahlen. Das bedeutet, dass es 8-mal mehr Speicher benötigt. Wir verwenden jedoch diese 64-Bit-Gleitkommazahlendarstellung zur Kodierung von 8 Werten. In der Tat sparen wir nur dann Speicher, wenn wir das komprimierte Bild in ein Array von 3-Bit-Ganzzahlen umwandeln. Wir könnten die Methode numpy.ndarray.astype verwenden. Eine 3-Bit-Ganzzahlendarstellung existiert jedoch nicht, und um die 8 Werte zu kodieren, müssten wir ebenfalls die vorzeichenlose 8-Bit-Ganzzahlendarstellung verwenden.

In der Praxis würde die Beobachtung eines Speicherzuwachses erfordern, dass das Originalbild in einer 64-Bit-Gleitkommazahlendarstellung vorliegt.

Verwandte Beispiele

Bildrauschen mit Dictionary Learning

Bildrauschen mit Dictionary Learning

Erkennung handschriftlicher Ziffern

Erkennung handschriftlicher Ziffern

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Segmentierung des Bildes von griechischen Münzen in Regionen

Segmentierung des Bildes von griechischen Münzen in Regionen