Hinweis

Zum Ende gehen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.

L1-basierte Modelle für dünnbesetzte Signale#

Das vorliegende Beispiel vergleicht drei l1-basierte Regressionsmodelle anhand eines synthetischen Signals, das aus dünnbesetzten und korrelierten Merkmalen gewonnen wird, die zusätzlich mit additivem Gaußschem Rauschen verrauscht sind.

Es ist bekannt, dass die Lasso-Schätzungen den Modellauswahlschätzungen nahe kommen, wenn die Daten-Dimensionen wachsen, vorausgesetzt, die irrelevanten Variablen sind nicht zu stark mit den relevanten korreliert. Bei korrelierten Merkmalen kann Lasso selbst kein korrektes Sparsity-Muster auswählen [1].

Hier vergleichen wir die Leistung der drei Modelle hinsichtlich des \(R^2\)-Scores, der Anpassungszeit und der Sparsity der geschätzten Koeffizienten im Vergleich zur Ground Truth.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Synthetischen Datensatz generieren#

Wir generieren einen Datensatz, bei dem die Anzahl der Stichproben geringer ist als die Gesamtzahl der Merkmale. Dies führt zu einem unterbestimmten System, d.h. die Lösung ist nicht eindeutig, und wir können daher kein Ordinary Least Squares allein anwenden. Regularisierung führt einen Strafterm zur Zielfunktion ein, der das Optimierungsproblem modifiziert und dazu beitragen kann, die unterbestimmte Natur des Systems zu mildern.

Das Ziel y ist eine Linearkombination mit alternierenden Vorzeichen von Sinussignalen. Nur die 10 niedrigsten von den 100 Frequenzen in X werden verwendet, um y zu generieren, während die restlichen Merkmale nicht informativ sind. Dies führt zu einem hochdimensionalen dünnbesetzten Merkmalsraum, in dem ein gewisses Maß an l1-Regularisierung notwendig ist.

import numpy as np

rng = np.random.RandomState(0)
n_samples, n_features, n_informative = 50, 100, 10
time_step = np.linspace(-2, 2, n_samples)
freqs = 2 * np.pi * np.sort(rng.rand(n_features)) / 0.01
X = np.zeros((n_samples, n_features))

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step)

idx = np.arange(n_features)
true_coef = (-1) ** idx * np.exp(-idx / 10)
true_coef[n_informative:] = 0  # sparsify coef
y = np.dot(X, true_coef)

Einige der informativen Merkmale haben ähnliche Frequenzen, um (Anti-)Korrelationen zu induzieren.

freqs[:n_informative]

array([ 2.9502547 , 11.8059798 , 12.63394388, 12.70359377, 24.62241605,
       37.84077985, 40.30506066, 44.63327171, 54.74495357, 59.02456369])

Eine zufällige Phase wird mit numpy.random.random_sample eingeführt und etwas Gaußsches Rauschen (implementiert durch numpy.random.normal) wird sowohl zu den Merkmalen als auch zum Ziel hinzugefügt.

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step + 2 * (rng.random_sample() - 0.5))
    X[:, i] += 0.2 * rng.normal(0, 1, n_samples)

y += 0.2 * rng.normal(0, 1, n_samples)

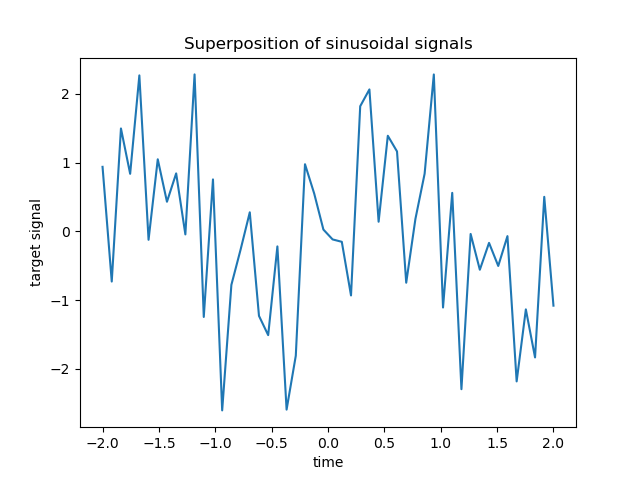
Solche dünnbesetzten, verrauschten und korrelierten Merkmale können beispielsweise von Sensor-Knoten gewonnen werden, die Umweltvariablen überwachen, da sie typischerweise ähnliche Werte je nach ihrer Position registrieren (räumliche Korrelationen). Wir können das Ziel visualisieren.

import matplotlib.pyplot as plt

plt.plot(time_step, y)
plt.ylabel("target signal")
plt.xlabel("time")
_ = plt.title("Superposition of sinusoidal signals")
Superposition of sinusoidal signals

Zur Vereinfachung teilen wir die Daten in Trainings- und Testdatensätze auf. In der Praxis sollte man eine TimeSeriesSplit Kreuzvalidierung verwenden, um die Varianz des Testscores abzuschätzen. Hier setzen wir shuffle="False", da wir keine Trainingsdaten verwenden dürfen, die die Testdaten übersteigen, wenn wir mit Daten umgehen, die eine zeitliche Beziehung aufweisen.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, shuffle=False)

Im Folgenden berechnen wir die Leistung von drei l1-basierten Modellen hinsichtlich des Gütefits \(R^2\)-Scores und der Anpassungszeit. Dann erstellen wir eine Grafik, um die Sparsity der geschätzten Koeffizienten im Vergleich zu den Ground-Truth-Koeffizienten zu vergleichen, und analysieren schließlich die vorherigen Ergebnisse.

Lasso#

In diesem Beispiel demonstrieren wir ein Lasso mit einem festen Wert des Regularisierungsparameters alpha. In der Praxis sollte der optimale Parameter alpha durch die Übergabe einer TimeSeriesSplit Kreuzvalidierungsstrategie an ein LassoCV ausgewählt werden. Um das Beispiel einfach und schnell ausführbar zu halten, setzen wir hier direkt den optimalen Wert für alpha.

from time import time

from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score

t0 = time()
lasso = Lasso(alpha=0.14).fit(X_train, y_train)
print(f"Lasso fit done in {(time() - t0):.3f}s")

y_pred_lasso = lasso.predict(X_test)
r2_score_lasso = r2_score(y_test, y_pred_lasso)
print(f"Lasso r^2 on test data : {r2_score_lasso:.3f}")

Lasso fit done in 0.001s
Lasso r^2 on test data : 0.480

Automatic Relevance Determination (ARD)#

Eine ARD-Regression ist die Bayes'sche Version des Lasso. Sie kann Intervallschätzungen für alle Parameter, einschließlich der Fehlervarianz, liefern, falls erforderlich. Sie ist eine geeignete Option, wenn die Signale Gaußsches Rauschen aufweisen. Sehen Sie sich das Beispiel Vergleich linearer Bayes'scher Regressoren für einen Vergleich von ARDRegression und BayesianRidge Regressoren an.

from sklearn.linear_model import ARDRegression

t0 = time()
ard = ARDRegression().fit(X_train, y_train)
print(f"ARD fit done in {(time() - t0):.3f}s")

y_pred_ard = ard.predict(X_test)
r2_score_ard = r2_score(y_test, y_pred_ard)
print(f"ARD r^2 on test data : {r2_score_ard:.3f}")

ARD fit done in 0.065s
ARD r^2 on test data : 0.543

ElasticNet#

ElasticNet ist ein Mittelweg zwischen Lasso und Ridge, da es eine L1- und eine L2-Strafe kombiniert. Der Grad der Regularisierung wird durch die beiden Hyperparameter l1_ratio und alpha gesteuert. Für l1_ratio = 0 ist die Strafe rein L2 und das Modell ist äquivalent zu einem Ridge. Ebenso ist l1_ratio = 1 eine reine L1-Strafe und das Modell ist äquivalent zu einem Lasso. Für 0 < l1_ratio < 1 ist die Strafe eine Kombination aus L1 und L2.

Wie zuvor trainieren wir das Modell mit festen Werten für alpha und l1_ratio. Zur Auswahl ihres optimalen Werts haben wir ein ElasticNetCV verwendet, das hier zur Vereinfachung des Beispiels nicht gezeigt wird.

from sklearn.linear_model import ElasticNet

t0 = time()
enet = ElasticNet(alpha=0.08, l1_ratio=0.5).fit(X_train, y_train)
print(f"ElasticNet fit done in {(time() - t0):.3f}s")

y_pred_enet = enet.predict(X_test)
r2_score_enet = r2_score(y_test, y_pred_enet)
print(f"ElasticNet r^2 on test data : {r2_score_enet:.3f}")

ElasticNet fit done in 0.001s
ElasticNet r^2 on test data : 0.636

Plot und Analyse der Ergebnisse#

In diesem Abschnitt verwenden wir eine Heatmap, um die Sparsity der wahren und geschätzten Koeffizienten der jeweiligen linearen Modelle zu visualisieren.

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from matplotlib.colors import SymLogNorm

df = pd.DataFrame(
    {
        "True coefficients": true_coef,
        "Lasso": lasso.coef_,
        "ARDRegression": ard.coef_,
        "ElasticNet": enet.coef_,
    }
)

plt.figure(figsize=(10, 6))
ax = sns.heatmap(
    df.T,
    norm=SymLogNorm(linthresh=10e-4, vmin=-1, vmax=1),
    cbar_kws={"label": "coefficients' values"},
    cmap="seismic_r",
)
plt.ylabel("linear model")
plt.xlabel("coefficients")
plt.title(
    f"Models' coefficients\nLasso $R^2$: {r2_score_lasso:.3f}, "
    f"ARD $R^2$: {r2_score_ard:.3f}, "
    f"ElasticNet $R^2$: {r2_score_enet:.3f}"
)
plt.tight_layout()
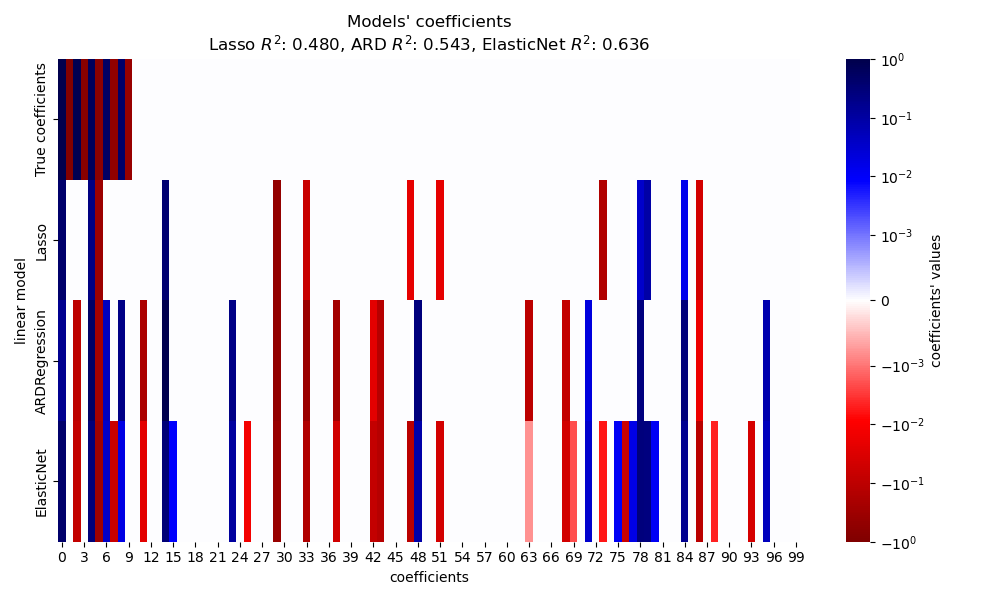
Models' coefficients Lasso $R^2$: 0.480, ARD $R^2$: 0.543, ElasticNet $R^2$: 0.636

Im vorliegenden Beispiel erzielt ElasticNet den besten Score und erfasst die meisten prädiktiven Merkmale, versagt aber dennoch bei der Ermittlung aller wahren Komponenten. Beachten Sie, dass sowohl ElasticNet als auch ARDRegression zu einem weniger dünnbesetzten Modell als ein Lasso führen.

Schlussfolgerungen#

Lasso ist dafür bekannt, dünnbesetzte Daten effektiv wiederherzustellen, aber er performt nicht gut bei stark korrelierten Merkmalen. Tatsächlich würde Lasso, wenn mehrere korrelierte Merkmale zum Ziel beitragen, schließlich nur eines davon auswählen. Bei dünnbesetzten, aber nicht korrelierten Merkmalen wäre ein Lasso-Modell besser geeignet.

ElasticNet führt eine gewisse Sparsity bei den Koeffizienten ein und reduziert ihre Werte auf Null. Daher ist das Modell bei korrelierten Merkmalen, die zum Ziel beitragen, immer noch in der Lage, ihre Gewichte zu reduzieren, ohne sie exakt auf Null zu setzen. Dies führt zu einem weniger dünnbesetzten Modell als ein reines Lasso und kann auch nicht-prädiktive Merkmale erfassen.

ARDRegression ist besser im Umgang mit Gaußschem Rauschen, kann aber immer noch nicht mit korrelierten Merkmalen umgehen und benötigt aufgrund der Anpassung eines Priors mehr Zeit.

Referenzen#

Gesamtlaufzeit des Skripts: (0 Minuten 0,475 Sekunden)

Verwandte Beispiele

Lasso auf dichten und spärlichen Daten

Lasso auf dichten und spärlichen Daten

Lasso, Lasso-LARS und Elastic Net Pfade

Lasso, Lasso-LARS und Elastic Net Pfade

Gemeinsame Merkmalsauswahl mit Multi-Task Lasso

Gemeinsame Merkmalsauswahl mit Multi-Task Lasso

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Galerie generiert von Sphinx-Gallery