Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Gaussian Mixture Model Selection#
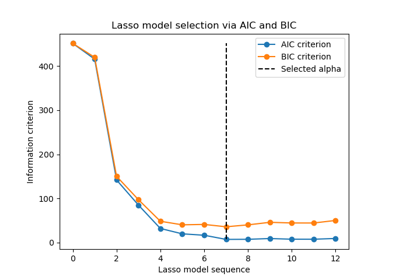
Dieses Beispiel zeigt, dass die Modellauswahl mit Gaußschen Mischmodellen (GMM) unter Verwendung von informationstheoretischen Kriterien durchgeführt werden kann. Die Modellauswahl betrifft sowohl den Kovarianztyp als auch die Anzahl der Komponenten im Modell.
In diesem Fall liefern sowohl das Akaike Information Criterion (AIC) als auch das Bayes Information Criterion (BIC) das richtige Ergebnis, wir zeigen jedoch nur letzteres, da BIC besser geeignet ist, das wahre Modell aus einer Menge von Kandidaten zu identifizieren. Im Gegensatz zu bayesianischen Verfahren sind solche Schlussfolgerungen vorab-frei.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Datengenerierung#
Wir generieren zwei Komponenten (jede enthält n_samples), indem wir zufällig die Standard-Normalverteilung abtasten, wie sie von numpy.random.randn zurückgegeben wird. Eine Komponente wird sphärisch gehalten, aber verschoben und skaliert. Die andere wird deformiert, um eine allgemeinere Kovarianzmatrix zu haben.
import numpy as np
n_samples = 500
np.random.seed(0)
C = np.array([[0.0, -0.1], [1.7, 0.4]])
component_1 = np.dot(np.random.randn(n_samples, 2), C) # general
component_2 = 0.7 * np.random.randn(n_samples, 2) + np.array([-4, 1]) # spherical
X = np.concatenate([component_1, component_2])
Wir können die verschiedenen Komponenten visualisieren
import matplotlib.pyplot as plt
plt.scatter(component_1[:, 0], component_1[:, 1], s=0.8)
plt.scatter(component_2[:, 0], component_2[:, 1], s=0.8)
plt.title("Gaussian Mixture components")
plt.axis("equal")
plt.show()

Modelltraining und -auswahl#
Wir variieren die Anzahl der Komponenten von 1 bis 6 und die zu verwendenden Typen von Kovarianzparametern
"full": Jede Komponente hat ihre eigene allgemeine Kovarianzmatrix."tied": Alle Komponenten teilen sich die gleiche allgemeine Kovarianzmatrix."diag": Jede Komponente hat ihre eigene diagonale Kovarianzmatrix."spherical": Jede Komponente hat ihre eigene einzelne Varianz.
Wir bewerten die verschiedenen Modelle und behalten das beste Modell (das niedrigste BIC). Dies geschieht durch die Verwendung von GridSearchCV und einer benutzerdefinierten Score-Funktion, die den negativen BIC-Score zurückgibt, da GridSearchCV darauf ausgelegt ist, einen Score zu maximieren (die Maximierung des negativen BIC ist äquivalent zur Minimierung des BIC).
Die besten Parameter und der beste Schätzer werden in best_parameters_ bzw. best_estimator_ gespeichert.
from sklearn.mixture import GaussianMixture
from sklearn.model_selection import GridSearchCV
def gmm_bic_score(estimator, X):
"""Callable to pass to GridSearchCV that will use the BIC score."""
# Make it negative since GridSearchCV expects a score to maximize
return -estimator.bic(X)
param_grid = {
"n_components": range(1, 7),
"covariance_type": ["spherical", "tied", "diag", "full"],
}
grid_search = GridSearchCV(
GaussianMixture(), param_grid=param_grid, scoring=gmm_bic_score
)
grid_search.fit(X)
Plotten der BIC-Werte#
Um das Plotten zu erleichtern, können wir ein pandas.DataFrame aus den Ergebnissen der Kreuzvalidierung erstellen, die durch die Gitter-Suche durchgeführt wurde. Wir kehren das Vorzeichen des BIC-Wertes um, um den Effekt der Minimierung zu zeigen.
import pandas as pd
df = pd.DataFrame(grid_search.cv_results_)[
["param_n_components", "param_covariance_type", "mean_test_score"]
]
df["mean_test_score"] = -df["mean_test_score"]
df = df.rename(
columns={
"param_n_components": "Number of components",
"param_covariance_type": "Type of covariance",
"mean_test_score": "BIC score",
}
)
df.sort_values(by="BIC score").head()
import seaborn as sns
sns.catplot(
data=df,
kind="bar",
x="Number of components",
y="BIC score",
hue="Type of covariance",
)
plt.show()

Im vorliegenden Fall hat das Modell mit 2 Komponenten und voller Kovarianz (das dem wahren generativen Modell entspricht) den niedrigsten BIC-Wert und wird daher von der Gitter-Suche ausgewählt.
Plotten des besten Modells#
Wir plotten eine Ellipse, um jede Gaußsche Komponente des ausgewählten Modells darzustellen. Zu diesem Zweck müssen die Eigenwerte der Kovarianzmatrizen, wie sie vom Attribut covariances_ zurückgegeben werden, ermittelt werden. Die Form solcher Matrizen hängt vom covariance_type ab.
"full": (n_components,n_features,n_features)"tied": (n_features,n_features)"diag": (n_components,n_features)"spherical": (n_components,)
from matplotlib.patches import Ellipse
from scipy import linalg
color_iter = sns.color_palette("tab10", 2)[::-1]
Y_ = grid_search.predict(X)
fig, ax = plt.subplots()
for i, (mean, cov, color) in enumerate(
zip(
grid_search.best_estimator_.means_,
grid_search.best_estimator_.covariances_,
color_iter,
)
):
v, w = linalg.eigh(cov)
if not np.any(Y_ == i):
continue
plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], 0.8, color=color)
angle = np.arctan2(w[0][1], w[0][0])
angle = 180.0 * angle / np.pi # convert to degrees
v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
ellipse = Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
ellipse.set_clip_box(fig.bbox)
ellipse.set_alpha(0.5)
ax.add_artist(ellipse)
plt.title(
f"Selected GMM: {grid_search.best_params_['covariance_type']} model, "
f"{grid_search.best_params_['n_components']} components"
)
plt.axis("equal")
plt.show()

Gesamtlaufzeit des Skripts: (0 Minuten 1,295 Sekunden)
Verwandte Beispiele
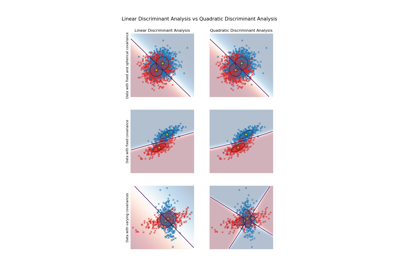
Lineare und Quadratische Diskriminanzanalyse mit Kovarianzellipsoid