Regularisierungspfad von L1-Logistischer Regression

Trainieren Sie L1-penalisierte logistische Regressionsmodelle für ein binäres Klassifizierungsproblem, das aus dem Iris-Datensatz abgeleitet ist.

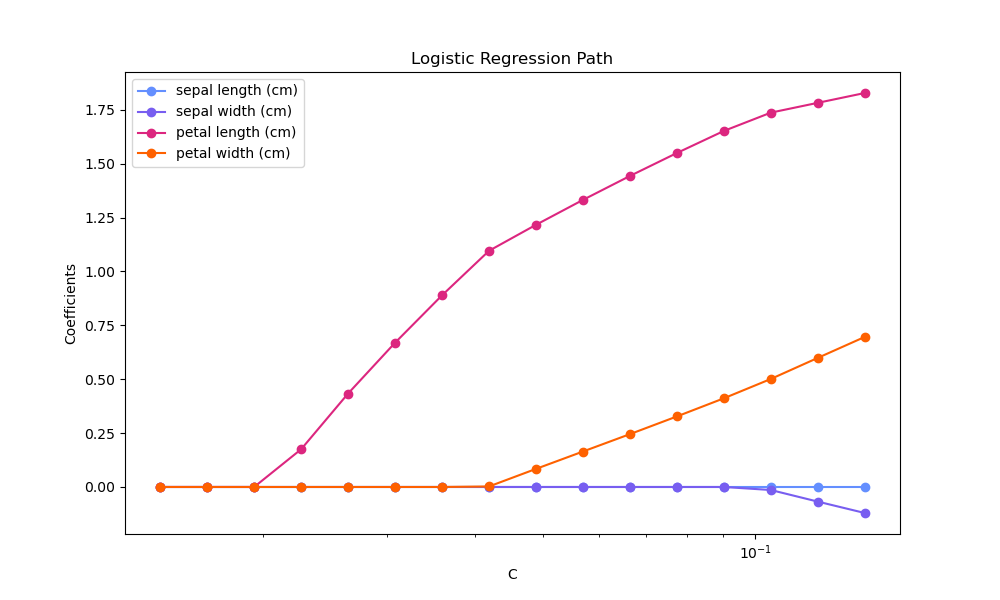
Die Modelle sind von der stärksten zur schwächsten Regularisierung geordnet. Die 4 Koeffizienten der Modelle werden gesammelt und als "Regularisierungspfad" dargestellt: auf der linken Seite der Abbildung (starke Regularisatoren) sind alle Koeffizienten exakt 0. Wenn die Regularisierung schrittweise gelockert wird, können die Koeffizienten nacheinander Nicht-Null-Werte annehmen.

Hier wählen wir den liblinear-Solver, da er die logistische Regressionsverlustfunktion mit einer nicht-glatten, sparsitätsfördernden L1-Strafe effizient optimieren kann.

Beachten Sie auch, dass wir einen niedrigen Wert für die Toleranz festgelegt haben, um sicherzustellen, dass das Modell konvergiert ist, bevor die Koeffizienten gesammelt werden.

Wir verwenden auch `warm_start=True`, was bedeutet, dass die Koeffizienten der Modelle wiederverwendet werden, um die nächste Modellanpassung zu initialisieren, um die Berechnung des vollständigen Pfades zu beschleunigen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Daten laden

from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names

Hier entfernen wir die dritte Klasse, um das Problem zu einer binären Klassifizierung zu machen.

X = X[y != 2]
y = y[y != 2]

Regularisierungspfad berechnen

import numpy as np

from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import l1_min_c

cs = l1_min_c(X, y, loss="log") * np.logspace(0, 1, 16)

Erstellen Sie eine Pipeline mit StandardScaler und LogisticRegression, um die Daten vor der Anpassung eines linearen Modells zu normalisieren, um die Konvergenz zu beschleunigen und die Koeffizienten vergleichbar zu machen. Da die Daten nun um 0 zentriert sind, müssen wir auch keinen Achsenabschnitt (Intercept) anpassen.

clf = make_pipeline(
    StandardScaler(),
    LogisticRegression(
        l1_ratio=1,
        solver="liblinear",
        tol=1e-6,
        max_iter=int(1e6),
        warm_start=True,
        fit_intercept=False,
    ),
)
coefs_ = []
for c in cs:
    clf.set_params(logisticregression__C=c)
    clf.fit(X, y)
    coefs_.append(clf["logisticregression"].coef_.ravel().copy())

coefs_ = np.array(coefs_)

Regularisierungspfad plotten

import matplotlib.pyplot as plt

# Colorblind-friendly palette (IBM Color Blind Safe palette)
colors = ["#648FFF", "#785EF0", "#DC267F", "#FE6100"]

plt.figure(figsize=(10, 6))
for i in range(coefs_.shape[1]):
    plt.semilogx(cs, coefs_[:, i], marker="o", color=colors[i], label=feature_names[i])

ymin, ymax = plt.ylim()
plt.xlabel("C")
plt.ylabel("Coefficients")
plt.title("Logistic Regression Path")
plt.legend()
plt.axis("tight")
plt.show()

Verwandte Beispiele

Ridge-Koeffizienten als Funktion der L2-Regularisierung

Ridge-Koeffizienten als Funktion der L2-Regularisierung

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

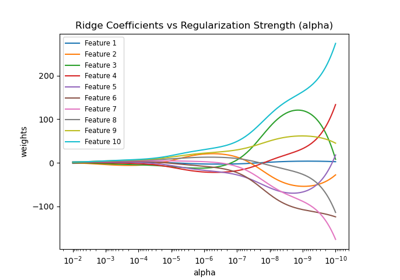
Ridge-Koeffizienten als Funktion der Regularisierung plotten

Ridge-Koeffizienten als Funktion der Regularisierung plotten

L1-Strafe und Sparsity in Logistischer Regression

L1-Strafe und Sparsity in Logistischer Regression