Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel in Ihrem Browser über JupyterLite oder Binder auszuführen.
Daten auf eine Normalverteilung abbilden#
Dieses Beispiel demonstriert die Verwendung von Box-Cox- und Yeo-Johnson-Transformationen durch PowerTransformer, um Daten aus verschiedenen Verteilungen auf eine Normalverteilung abzubilden.
Die Potenztransformation ist nützlich als Transformation in Modellierungsproblemen, bei denen Homoskedastizität und Normalität erwünscht sind. Im Folgenden finden Sie Beispiele für Box-Cox und Yeo-Johnson, die auf sechs verschiedene Wahrscheinlichkeitsverteilungen angewendet werden: Lognormal, Chi-Quadrat, Weibull, Gauß, Gleichverteilung und Bimodal.
Beachten Sie, dass die Transformationen die Daten erfolgreich auf eine Normalverteilung abbilden, wenn sie auf bestimmte Datensätze angewendet werden, aber bei anderen unwirksam sind. Dies unterstreicht die Bedeutung der Visualisierung der Daten vor und nach der Transformation.
Beachten Sie auch, dass Box-Cox zwar bei lognormalen und Chi-Quadrat-Verteilungen besser zu funktionieren scheint als Yeo-Johnson, aber bedenken Sie, dass Box-Cox keine Eingaben mit negativen Werten unterstützt.
Zum Vergleich fügen wir auch die Ausgabe von QuantileTransformer hinzu. Diese kann jede beliebige Verteilung in eine Gaußsche Verteilung erzwingen, vorausgesetzt, es gibt genügend Trainingsstichproben (Tausende). Da es sich um eine nicht-parametrische Methode handelt, ist sie schwieriger zu interpretieren als die parametrischen Methoden (Box-Cox und Yeo-Johnson).
Bei „kleinen“ Datensätzen (weniger als einige hundert Punkte) neigt der Quantiltransformator zur Überanpassung. Die Verwendung der Potenztransformation wird dann empfohlen.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PowerTransformer, QuantileTransformer
N_SAMPLES = 1000
FONT_SIZE = 6
BINS = 30
rng = np.random.RandomState(304)
bc = PowerTransformer(method="box-cox")
yj = PowerTransformer(method="yeo-johnson")
# n_quantiles is set to the training set size rather than the default value
# to avoid a warning being raised by this example
qt = QuantileTransformer(
n_quantiles=500, output_distribution="normal", random_state=rng
)
size = (N_SAMPLES, 1)
# lognormal distribution
X_lognormal = rng.lognormal(size=size)
# chi-squared distribution
df = 3
X_chisq = rng.chisquare(df=df, size=size)
# weibull distribution
a = 50
X_weibull = rng.weibull(a=a, size=size)
# gaussian distribution
loc = 100
X_gaussian = rng.normal(loc=loc, size=size)
# uniform distribution
X_uniform = rng.uniform(low=0, high=1, size=size)
# bimodal distribution
loc_a, loc_b = 100, 105
X_a, X_b = rng.normal(loc=loc_a, size=size), rng.normal(loc=loc_b, size=size)
X_bimodal = np.concatenate([X_a, X_b], axis=0)
# create plots
distributions = [
("Lognormal", X_lognormal),
("Chi-squared", X_chisq),
("Weibull", X_weibull),
("Gaussian", X_gaussian),
("Uniform", X_uniform),
("Bimodal", X_bimodal),
]
colors = ["#D81B60", "#0188FF", "#FFC107", "#B7A2FF", "#000000", "#2EC5AC"]
fig, axes = plt.subplots(nrows=8, ncols=3, figsize=plt.figaspect(2))
axes = axes.flatten()
axes_idxs = [
(0, 3, 6, 9),
(1, 4, 7, 10),
(2, 5, 8, 11),
(12, 15, 18, 21),
(13, 16, 19, 22),
(14, 17, 20, 23),
]
axes_list = [(axes[i], axes[j], axes[k], axes[l]) for (i, j, k, l) in axes_idxs]
for distribution, color, axes in zip(distributions, colors, axes_list):
name, X = distribution
X_train, X_test = train_test_split(X, test_size=0.5)
# perform power transforms and quantile transform
X_trans_bc = bc.fit(X_train).transform(X_test)
lmbda_bc = round(bc.lambdas_[0], 2)
X_trans_yj = yj.fit(X_train).transform(X_test)
lmbda_yj = round(yj.lambdas_[0], 2)
X_trans_qt = qt.fit(X_train).transform(X_test)
ax_original, ax_bc, ax_yj, ax_qt = axes
ax_original.hist(X_train, color=color, bins=BINS)
ax_original.set_title(name, fontsize=FONT_SIZE)
ax_original.tick_params(axis="both", which="major", labelsize=FONT_SIZE)
for ax, X_trans, meth_name, lmbda in zip(
(ax_bc, ax_yj, ax_qt),
(X_trans_bc, X_trans_yj, X_trans_qt),
("Box-Cox", "Yeo-Johnson", "Quantile transform"),
(lmbda_bc, lmbda_yj, None),
):
ax.hist(X_trans, color=color, bins=BINS)
title = "After {}".format(meth_name)
if lmbda is not None:
title += "\n$\\lambda$ = {}".format(lmbda)
ax.set_title(title, fontsize=FONT_SIZE)
ax.tick_params(axis="both", which="major", labelsize=FONT_SIZE)
ax.set_xlim([-3.5, 3.5])
plt.tight_layout()
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 1,893 Sekunden)
Verwandte Beispiele

Vergleich der Auswirkungen verschiedener Skalierer auf Daten mit Ausreißern
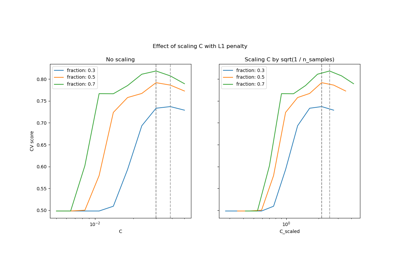
Skalierung des Regularisierungsparameters für SVCs
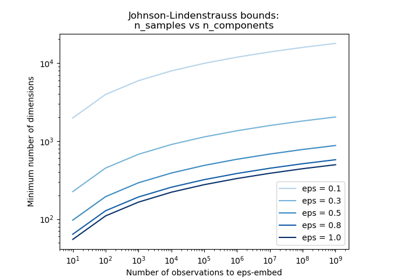
Die Johnson-Lindenstrauss-Schranke für Einbettung mit zufälligen Projektionen