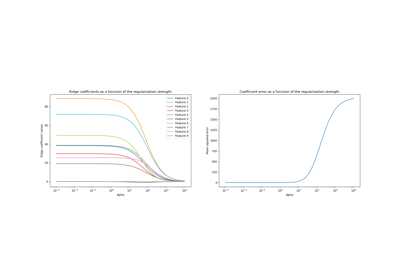
Plot Ridge-Koeffizienten als Funktion der Regularisierung

Zeigt den Effekt von Kollinearität auf die Koeffizienten eines Schätzers.

Ridge Regression ist der in diesem Beispiel verwendete Schätzer. Jede Farbe repräsentiert eine andere Komponente des Koeffizientenvektors, und dies wird als Funktion des Regularisierungsparameters dargestellt.

Dieses Beispiel zeigt auch die Nützlichkeit der Anwendung der Ridge-Regression auf stark schlecht konditionierte Matrizen. Bei solchen Matrizen kann eine geringfügige Änderung der Zielvariablen zu großen Varianzen in den berechneten Gewichten führen. In solchen Fällen ist es nützlich, eine bestimmte Regularisierung (alpha) festzulegen, um diese Variation (Rauschen) zu reduzieren.

Wenn alpha sehr groß ist, dominiert der Regularisierungseffekt die quadratische Verlustfunktion und die Koeffizienten tendieren gegen null. Am Ende des Pfades, wenn alpha gegen null geht und die Lösung gegen die gewöhnliche kleinste Quadrate tendiert, zeigen die Koeffizienten große Oszillationen. In der Praxis ist es notwendig, alpha so abzustimmen, dass ein Gleichgewicht zwischen beidem aufrechterhalten wird.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn import linear_model

# X is the 10x10 Hilbert matrix
X = 1.0 / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)

Pfade berechnen

n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)

coefs = []
for a in alphas:
    ridge = linear_model.Ridge(alpha=a, fit_intercept=False)
    ridge.fit(X, y)
    coefs.append(ridge.coef_)

Ergebnisse anzeigen

ax = plt.gca()

ax.plot(alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Ridge Coefficients vs Regularization Strength (alpha)")
plt.axis("tight")
plt.legend(
    [f"Feature {i + 1}" for i in range(X.shape[1])], loc="best", fontsize="small"
)
plt.show()

Verwandte Beispiele

Ridge-Koeffizienten als Funktion der L2-Regularisierung

Ridge-Koeffizienten als Funktion der L2-Regularisierung

HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern

HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Häufige Fallstricke bei der Interpretation von Koeffizienten linearer Modelle

Häufige Fallstricke bei der Interpretation von Koeffizienten linearer Modelle