Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Wahrscheinlichkeitskalibrierung für 3-Klassen-Klassifizierung#
Dieses Beispiel veranschaulicht, wie die Sigmoid- Kalibrierung die vorhergesagten Wahrscheinlichkeiten für ein 3-Klassen-Klassifizierungsproblem verändert. Dargestellt ist das Standard-2-Simplex, bei dem die drei Ecken den drei Klassen entsprechen. Pfeile zeigen von den vom unkalibrierten Klassifikator vorhergesagten Wahrscheinlichkeitsvektoren zu den vom selben Klassifikator nach der Sigmoid-Kalibrierung auf einem zurückgehaltenen Validierungsdatensatz vorhergesagten Wahrscheinlichkeitsvektoren. Farben zeigen die wahre Klasse einer Instanz an (rot: Klasse 1, grün: Klasse 2, blau: Klasse 3).
Daten#
Im Folgenden generieren wir einen Klassifizierungsdatensatz mit 2000 Stichproben, 2 Merkmalen und 3 Zielklassen. Wir teilen die Daten dann wie folgt auf:
train: 600 Stichproben (zum Trainieren des Klassifikators)
valid: 400 Stichproben (zur Kalibrierung vorhergesagter Wahrscheinlichkeiten)
test: 1000 Stichproben
Beachten Sie, dass wir auch X_train_valid und y_train_valid erstellen, die sowohl die Trainings- als auch die Validierungsuntergruppen umfassen. Dies wird verwendet, wenn wir nur den Klassifikator trainieren, aber die vorhergesagten Wahrscheinlichkeiten nicht kalibrieren möchten.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from sklearn.datasets import make_blobs
np.random.seed(0)
X, y = make_blobs(
n_samples=2000, n_features=2, centers=3, random_state=42, cluster_std=5.0
)
X_train, y_train = X[:600], y[:600]
X_valid, y_valid = X[600:1000], y[600:1000]
X_train_valid, y_train_valid = X[:1000], y[:1000]
X_test, y_test = X[1000:], y[1000:]
Anpassen und Kalibrierung#
Zuerst trainieren wir einen RandomForestClassifier mit 25 Basisschätzern (Bäumen) auf den verketteten Trainings- und Validierungsdaten (1000 Stichproben). Dies ist der unkalibrierte Klassifikator.
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train_valid, y_train_valid)
Um den kalibrierten Klassifikator zu trainieren, beginnen wir mit demselben RandomForestClassifier, trainieren ihn aber nur mit der Trainingsdatenuntergruppe (600 Stichproben) und kalibrieren ihn dann mit method='sigmoid' unter Verwendung der Validierungsdatenuntergruppe (400 Stichproben) in einem 2-stufigen Prozess.
from sklearn.calibration import CalibratedClassifierCV
from sklearn.frozen import FrozenEstimator
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train, y_train)
cal_clf = CalibratedClassifierCV(FrozenEstimator(clf), method="sigmoid")
cal_clf.fit(X_valid, y_valid)
Wahrscheinlichkeiten vergleichen#
Im Folgenden plotten wir ein 2-Simplex mit Pfeilen, die die Änderung der vorhergesagten Wahrscheinlichkeiten der Teststichproben zeigen.
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 10))
colors = ["r", "g", "b"]
clf_probs = clf.predict_proba(X_test)
cal_clf_probs = cal_clf.predict_proba(X_test)
# Plot arrows
for i in range(clf_probs.shape[0]):
plt.arrow(
clf_probs[i, 0],
clf_probs[i, 1],
cal_clf_probs[i, 0] - clf_probs[i, 0],
cal_clf_probs[i, 1] - clf_probs[i, 1],
color=colors[y_test[i]],
head_width=1e-2,
)
# Plot perfect predictions, at each vertex
plt.plot([1.0], [0.0], "ro", ms=20, label="Class 1")
plt.plot([0.0], [1.0], "go", ms=20, label="Class 2")
plt.plot([0.0], [0.0], "bo", ms=20, label="Class 3")
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
# Annotate points 6 points around the simplex, and mid point inside simplex
plt.annotate(
r"($\frac{1}{3}$, $\frac{1}{3}$, $\frac{1}{3}$)",
xy=(1.0 / 3, 1.0 / 3),
xytext=(1.0 / 3, 0.23),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.plot([1.0 / 3], [1.0 / 3], "ko", ms=5)
plt.annotate(
r"($\frac{1}{2}$, $0$, $\frac{1}{2}$)",
xy=(0.5, 0.0),
xytext=(0.5, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $\frac{1}{2}$, $\frac{1}{2}$)",
xy=(0.0, 0.5),
xytext=(0.1, 0.5),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($\frac{1}{2}$, $\frac{1}{2}$, $0$)",
xy=(0.5, 0.5),
xytext=(0.6, 0.6),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $0$, $1$)",
xy=(0, 0),
xytext=(0.1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($1$, $0$, $0$)",
xy=(1, 0),
xytext=(1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $1$, $0$)",
xy=(0, 1),
xytext=(0.1, 1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
# Add grid
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Change of predicted probabilities on test samples after sigmoid calibration")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
_ = plt.legend(loc="best")
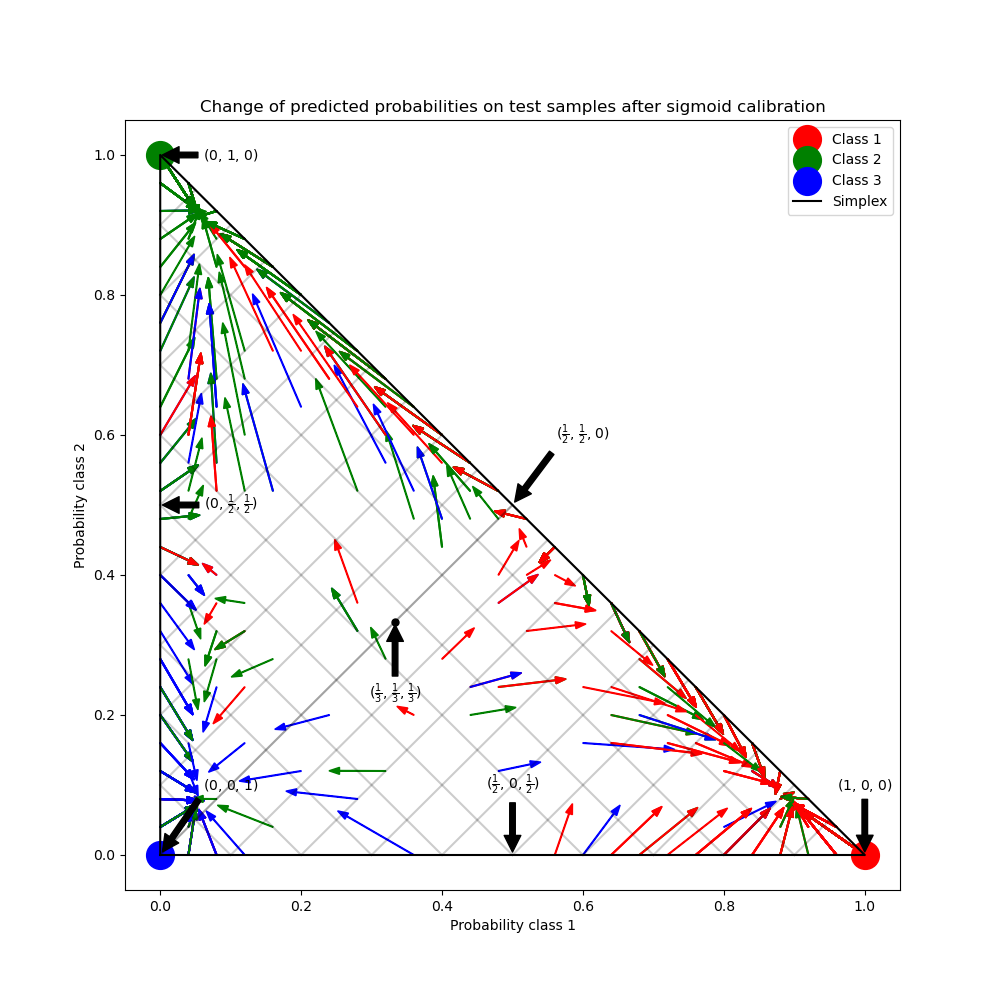
In der obigen Abbildung repräsentiert jeder Eckpunkt des Simplex eine perfekt vorhergesagte Klasse (z.B. 1, 0, 0). Der Mittelpunkt innerhalb des Simplex repräsentiert die Vorhersage der drei Klassen mit gleicher Wahrscheinlichkeit (d.h. 1/3, 1/3, 1/3). Jeder Pfeil beginnt bei den unkalibrierten Wahrscheinlichkeiten und endet mit der Pfeilspitze bei der kalibrierten Wahrscheinlichkeit. Die Farbe des Pfeils repräsentiert die wahre Klasse dieser Teststichprobe.
Der unkalibrierte Klassifikator ist übermäßig zuversichtlich in seinen Vorhersagen und verursacht einen hohen Log-Verlust. Der kalibrierte Klassifikator verursacht einen niedrigeren Log-Verlust aufgrund von zwei Faktoren. Erstens zeigen die Pfeile in der obigen Abbildung im Allgemeinen weg von den Rändern des Simplex, wo die Wahrscheinlichkeit einer Klasse 0 ist. Zweitens zeigt ein großer Teil der Pfeile in Richtung der wahren Klasse, z.B. grüne Pfeile (Stichproben, bei denen die wahre Klasse 'grün' ist) zeigen im Allgemeinen zum grünen Eckpunkt. Dies führt zu weniger übermäßig zuversichtlichen, 0 vorhergesagten Wahrscheinlichkeiten und gleichzeitig zu einer Erhöhung der vorhergesagten Wahrscheinlichkeiten der korrekten Klasse. Daher liefert der kalibrierte Klassifikator genauere vorhergesagte Wahrscheinlichkeiten, die einen niedrigeren Log-Verlust verursachen.
Wir können dies objektiv vergleichen, indem wir den Log-Verlust der unkalibrierten und kalibrierten Klassifikatoren auf den Vorhersagen der 1000 Teststichproben vergleichen. Beachten Sie, dass eine Alternative darin bestünde, die Anzahl der Basisschätzer (Bäume) des RandomForestClassifier zu erhöhen, was zu einer ähnlichen Verringerung des Log-Verlusts führen würde.
Log-loss of:
- uncalibrated classifier: 1.327
- calibrated classifier: 0.549
Wir können die Kalibrierung auch mit dem Brier-Score für probabilistische Vorhersagen bewerten (niedriger ist besser, möglicher Bereich ist [0, 2])
from sklearn.metrics import brier_score_loss
loss = brier_score_loss(y_test, clf_probs)
cal_loss = brier_score_loss(y_test, cal_clf_probs)
print("Brier score of")
print(f" - uncalibrated classifier: {loss:.3f}")
print(f" - calibrated classifier: {cal_loss:.3f}")
Brier score of
- uncalibrated classifier: 0.308
- calibrated classifier: 0.310
Laut Brier-Score ist der kalibrierte Klassifikator nicht besser als das ursprüngliche Modell.
Schließlich generieren wir ein Gitter möglicher unkalibrierter Wahrscheinlichkeiten über dem 2-Simplex, berechnen die entsprechenden kalibrierten Wahrscheinlichkeiten und plotten für jede Pfeile. Die Pfeile sind entsprechend der höchsten unkalibrierten Wahrscheinlichkeit gefärbt. Dies veranschaulicht die erlernte Kalibrierungskarte.
plt.figure(figsize=(10, 10))
# Generate grid of probability values
p1d = np.linspace(0, 1, 20)
p0, p1 = np.meshgrid(p1d, p1d)
p2 = 1 - p0 - p1
p = np.c_[p0.ravel(), p1.ravel(), p2.ravel()]
p = p[p[:, 2] >= 0]
# Use the three class-wise calibrators to compute calibrated probabilities
calibrated_classifier = cal_clf.calibrated_classifiers_[0]
prediction = np.vstack(
[
calibrator.predict(this_p)
for calibrator, this_p in zip(calibrated_classifier.calibrators, p.T)
]
).T
# Re-normalize the calibrated predictions to make sure they stay inside the
# simplex. This same renormalization step is performed internally by the
# predict method of CalibratedClassifierCV on multiclass problems.
prediction /= prediction.sum(axis=1)[:, None]
# Plot changes in predicted probabilities induced by the calibrators
for i in range(prediction.shape[0]):
plt.arrow(
p[i, 0],
p[i, 1],
prediction[i, 0] - p[i, 0],
prediction[i, 1] - p[i, 1],
head_width=1e-2,
color=colors[np.argmax(p[i])],
)
# Plot the boundaries of the unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Learned sigmoid calibration map")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.show()
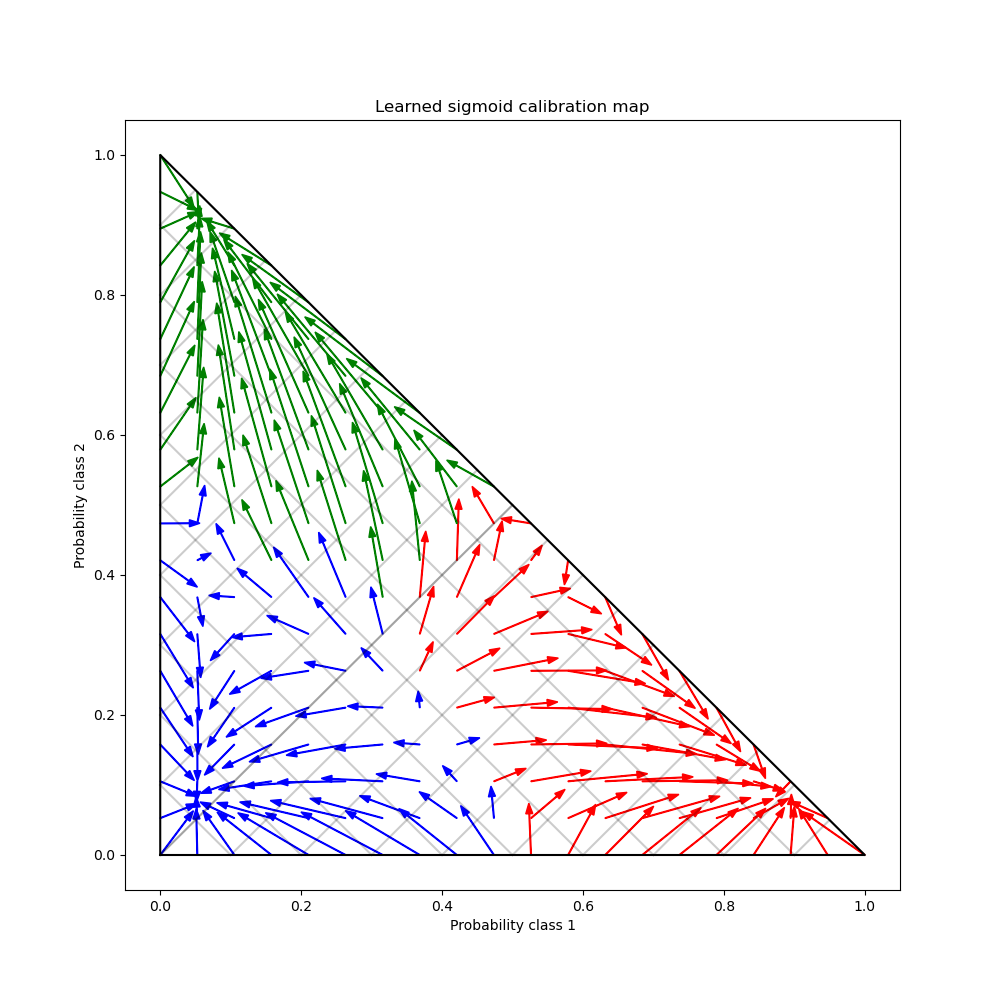
Man kann beobachten, dass der Kalibrator im Durchschnitt hoch zuversichtliche Vorhersagen von den Grenzen des Simplex weg schiebt, während er gleichzeitig unsichere Vorhersagen in einen von drei Modi bewegt, einen für jede Klasse. Wir können auch beobachten, dass die Abbildung nicht symmetrisch ist. Darüber hinaus scheinen einige Pfeile Klassenzuweisungsgrenzen zu überschreiten, was nicht unbedingt das ist, was man von einer Kalibrierungskarte erwarten würde, da dies bedeutet, dass sich einige vorhergesagte Klassen nach der Kalibrierung ändern werden.
Alles in allem sollte die One-vs-Rest-Mehrklassen-Kalibrierungsstrategie, die in CalibratedClassifierCV implementiert ist, nicht blind vertraut werden.
Gesamtlaufzeit des Skripts: (0 Minuten 1,214 Sekunden)
Verwandte Beispiele
Wahrscheinlichkeitskalibrierung von Klassifikatoren