Verschiedene agglomerative Clusterbildungen auf einer 2D-Einbettung von Ziffern

Eine Veranschaulichung verschiedener Linkage-Optionen für agglomerative Clusterbildung auf einer 2D-Einbettung des Datensatzes von Ziffern.

Das Ziel dieses Beispiels ist es, intuitiv zu zeigen, wie die Metriken funktionieren, und nicht, gute Cluster für die Ziffern zu finden. Deshalb arbeitet das Beispiel auf einer 2D-Einbettung.

Was dieses Beispiel uns zeigt, ist das Verhalten "die Reichen werden reicher" der agglomerativen Clusterbildung, die dazu neigt, ungleiche Clustergrößen zu erzeugen.

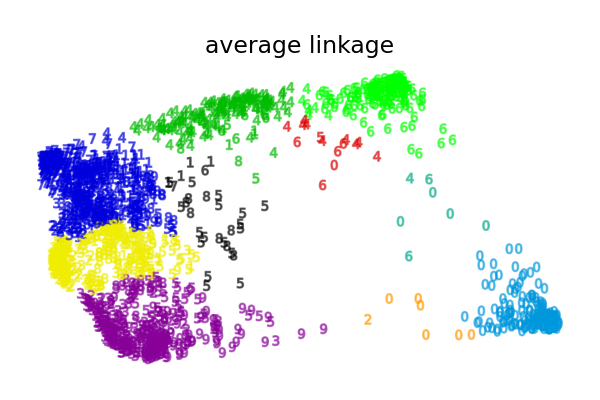
Dieses Verhalten ist bei der "average linkage"-Strategie ausgeprägt, die mit einigen Clustern mit wenigen Datenpunkten endet.

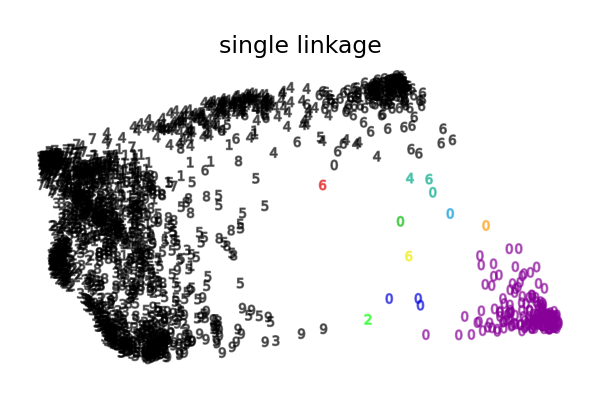
Der Fall der "single linkage" ist noch pathologischer, mit einem sehr großen Cluster, der die meisten Ziffern abdeckt, einem Zwischencluster (sauber) mit den meisten Nullen und allen anderen Clustern, die aus Rauschpunkten am Rand gezogen werden.

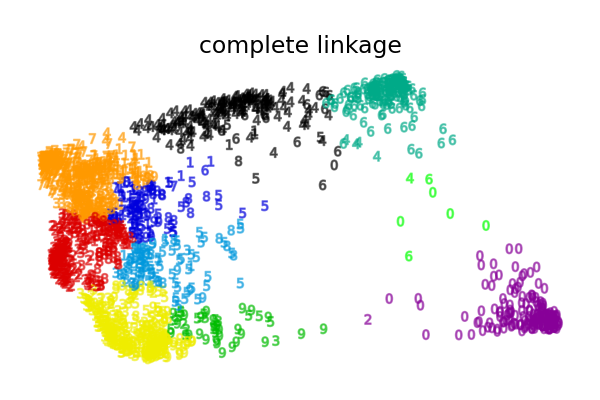
Die anderen Linkage-Strategien führen zu gleichmäßiger verteilten Clustern, die daher wahrscheinlich weniger empfindlich auf eine zufällige Stichprobennahme des Datensatzes reagieren.

• 
• 
• 
• 

Computing embedding
Done.
ward :  0.05s
average :       0.05s
complete :      0.05s
single :        0.02s

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

from time import time

import numpy as np
from matplotlib import pyplot as plt

from sklearn import datasets, manifold

digits = datasets.load_digits()
X, y = digits.data, digits.target
n_samples, n_features = X.shape

np.random.seed(0)


# ----------------------------------------------------------------------
# Visualize the clustering
def plot_clustering(X_red, labels, title=None):
    x_min, x_max = np.min(X_red, axis=0), np.max(X_red, axis=0)
    X_red = (X_red - x_min) / (x_max - x_min)

    plt.figure(figsize=(6, 4))
    for digit in digits.target_names:
        plt.scatter(
            *X_red[y == digit].T,
            marker=f"${digit}$",
            s=50,
            c=plt.cm.nipy_spectral(labels[y == digit] / 10),
            alpha=0.5,
        )

    plt.xticks([])
    plt.yticks([])
    if title is not None:
        plt.title(title, size=17)
    plt.axis("off")
    plt.tight_layout(rect=[0, 0.03, 1, 0.95])


# ----------------------------------------------------------------------
# 2D embedding of the digits dataset
print("Computing embedding")
X_red = manifold.SpectralEmbedding(n_components=2).fit_transform(X)
print("Done.")

from sklearn.cluster import AgglomerativeClustering

for linkage in ("ward", "average", "complete", "single"):
    clustering = AgglomerativeClustering(linkage=linkage, n_clusters=10)
    t0 = time()
    clustering.fit(X_red)
    print("%s :\t%.2fs" % (linkage, time() - t0))

    plot_clustering(X_red, clustering.labels_, "%s linkage" % linkage)


plt.show()

Verwandte Beispiele

Vergleich verschiedener hierarchischer Linkage-Methoden auf Toy-Datensätzen

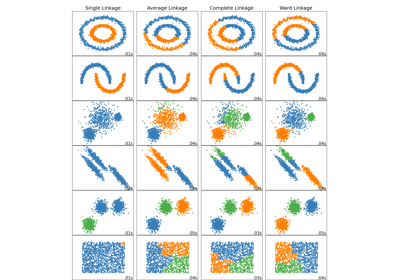
Vergleich verschiedener hierarchischer Linkage-Methoden auf Toy-Datensätzen

Manifold Learning auf handschriftlichen Ziffern: Locally Linear Embedding, Isomap…

Mannigfaltigkeitslernen auf handgeschriebenen Ziffern: Locally Linear Embedding, Isomap...

Hierarchisches Clustering mit und ohne Struktur

Hierarchisches Clustering mit und ohne Struktur

Visualisierung der Aktienmarktstruktur

Visualisierung der Aktienmarktstruktur