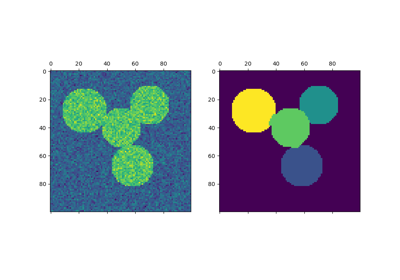
Segmentierung des Bildes griechischer Münzen in Regionen

Dieses Beispiel verwendet Spektrales Clustering auf einem Graphen, der aus der Voxel-zu-Voxel-Differenz eines Bildes erstellt wurde, um dieses Bild in mehrere teilweise homogene Regionen aufzuteilen.

Dieses Verfahren (spektrales Clustering auf einem Bild) ist eine effiziente Näherungslösung für die Suche nach normalisierten Graph-Schnitten.

Es gibt drei Optionen zur Zuweisung von Labels

• ‘kmeans’ Spektrales Clustering clustert Stichproben im Einbettungsraum unter Verwendung eines KMeans-Algorithmus

• ‘discrete’ Iterativ wird nach der Partition gesucht, die dem Einbettungsraum des spektralen Clusterings am nächsten liegt.

• ‘cluster_qr’ weist Labels unter Verwendung der QR-Faktorisierung mit Pivoting zu, die die Partition im Einbettungsraum direkt bestimmt.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np
from scipy.ndimage import gaussian_filter
from skimage.data import coins
from skimage.transform import rescale

from sklearn.cluster import spectral_clustering
from sklearn.feature_extraction import image

# load the coins as a numpy array
orig_coins = coins()

# Resize it to 20% of the original size to speed up the processing
# Applying a Gaussian filter for smoothing prior to down-scaling
# reduces aliasing artifacts.
smoothened_coins = gaussian_filter(orig_coins, sigma=2)
rescaled_coins = rescale(smoothened_coins, 0.2, mode="reflect", anti_aliasing=False)

# Convert the image into a graph with the value of the gradient on the
# edges.
graph = image.img_to_graph(rescaled_coins)

# Take a decreasing function of the gradient: an exponential
# The smaller beta is, the more independent the segmentation is of the
# actual image. For beta=1, the segmentation is close to a voronoi
beta = 10
eps = 1e-6
graph.data = np.exp(-beta * graph.data / graph.data.std()) + eps

# The number of segmented regions to display needs to be chosen manually.
# The current version of 'spectral_clustering' does not support determining
# the number of good quality clusters automatically.
n_regions = 26

Berechnung und Visualisierung der resultierenden Regionen

# Computing a few extra eigenvectors may speed up the eigen_solver.
# The spectral clustering quality may also benefit from requesting
# extra regions for segmentation.
n_regions_plus = 3

# Apply spectral clustering using the default eigen_solver='arpack'.
# Any implemented solver can be used: eigen_solver='arpack', 'lobpcg', or 'amg'.
# Choosing eigen_solver='amg' requires an extra package called 'pyamg'.
# The quality of segmentation and the speed of calculations is mostly determined
# by the choice of the solver and the value of the tolerance 'eigen_tol'.
# TODO: varying eigen_tol seems to have no effect for 'lobpcg' and 'amg' #21243.
for assign_labels in ("kmeans", "discretize", "cluster_qr"):
    t0 = time.time()
    labels = spectral_clustering(
        graph,
        n_clusters=(n_regions + n_regions_plus),
        eigen_tol=1e-7,
        assign_labels=assign_labels,
        random_state=42,
    )

    t1 = time.time()
    labels = labels.reshape(rescaled_coins.shape)
    plt.figure(figsize=(5, 5))
    plt.imshow(rescaled_coins, cmap=plt.cm.gray)

    plt.xticks(())
    plt.yticks(())
    title = "Spectral clustering: %s, %.2fs" % (assign_labels, (t1 - t0))
    print(title)
    plt.title(title)
    for l in range(n_regions):
        colors = [plt.cm.nipy_spectral((l + 4) / float(n_regions + 4))]
        plt.contour(labels == l, colors=colors)
        # To view individual segments as appear comment in plt.pause(0.5)
plt.show()

# TODO: After #21194 is merged and #21243 is fixed, check which eigen_solver
# is the best and set eigen_solver='arpack', 'lobpcg', or 'amg' and eigen_tol
# explicitly in this example.

• 
• 
• 

Spectral clustering: kmeans, 1.59s
Spectral clustering: discretize, 1.46s
Spectral clustering: cluster_qr, 1.45s

Verwandte Beispiele

Spektrales Clustering für Bildsegmentierung

Spektrales Clustering für Bildsegmentierung

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Visualisierung der Aktienmarktstruktur

Visualisierung der Aktienmarktstruktur

Bildrauschen mit Dictionary Learning

Bildrauschen mit Dictionary Learning