Agglomerative Clustering mit verschiedenen Metriken

Demonstriert den Effekt unterschiedlicher Metriken auf das hierarchische Clustering.

Das Beispiel wurde entwickelt, um den Effekt der Wahl unterschiedlicher Metriken zu zeigen. Es wird auf Wellenformen angewendet, die als hochdimensionale Vektoren betrachtet werden können. Tatsächlich ist der Unterschied zwischen Metriken in hohen Dimensionen in der Regel ausgeprägter (insbesondere für Euklidisch und Cityblock).

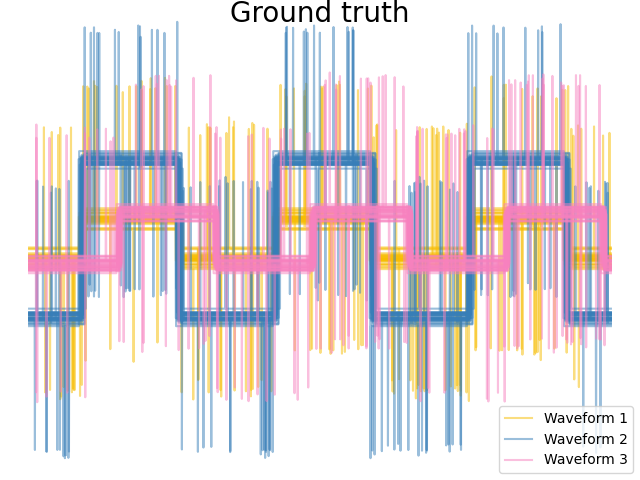
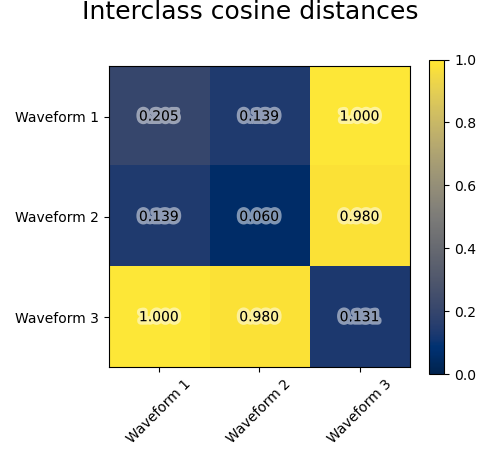
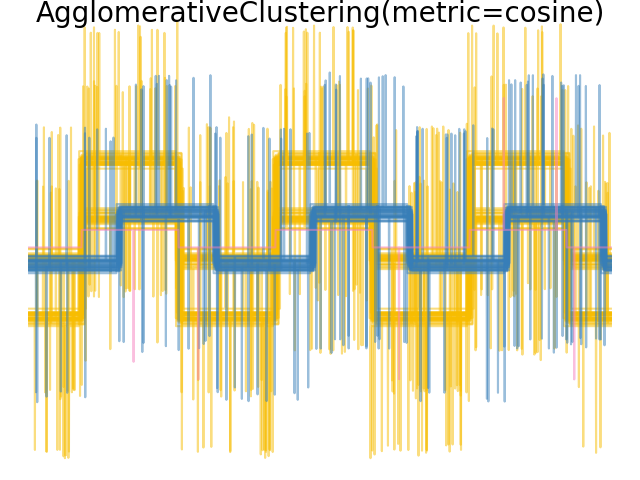
Wir generieren Daten aus drei Gruppen von Wellenformen. Zwei der Wellenformen (Wellenform 1 und Wellenform 2) sind proportional zueinander. Die Kosinus-Distanz ist invariant gegenüber einer Skalierung der Daten, daher kann sie diese beiden Wellenformen nicht unterscheiden. Selbst ohne Rauschen wird das Clustering mit dieser Distanz Wellenform 1 und 2 nicht trennen.

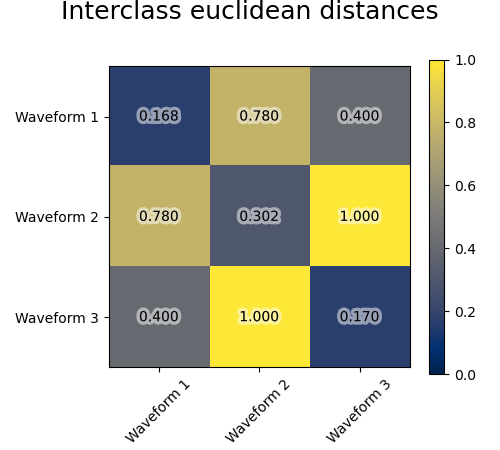
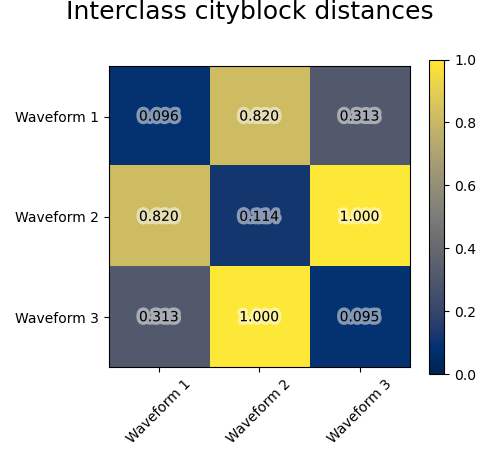
Wir fügen diesen Wellenformen Beobachtungsrauschen hinzu. Wir generieren sehr spärliches Rauschen: nur 6% der Zeitpunkte enthalten Rauschen. Als Ergebnis ist die L1-Norm dieses Rauschens (d. h. die "Cityblock"-Distanz) viel kleiner als seine L2-Norm ("Euklidische" Distanz). Dies ist in den inter-Klassen-Distanzmatrizen ersichtlich: Die Werte auf der Diagonale, die die Streuung der Klasse charakterisieren, sind für die Euklidische Distanz viel größer als für die Cityblock-Distanz.

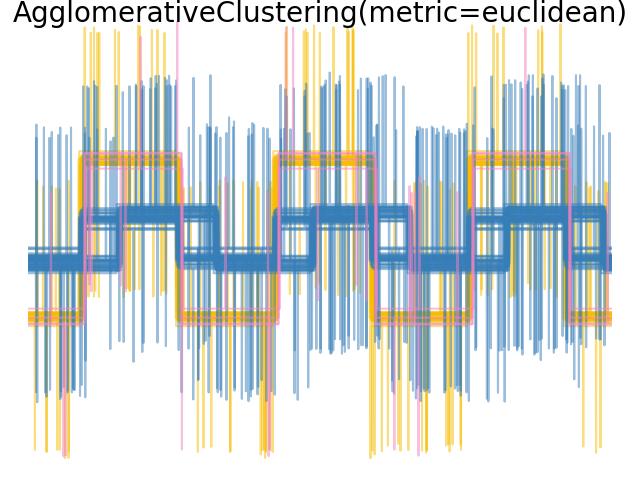
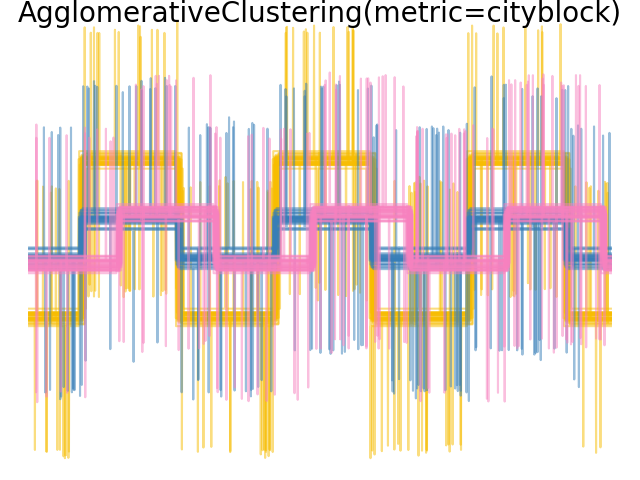
Wenn wir das Clustering auf die Daten anwenden, stellen wir fest, dass das Clustering das widerspiegelt, was in den Distanzmatrizen vorhanden war. Tatsächlich sind für die Euklidische Distanz die Klassen aufgrund des Rauschens schlecht getrennt, und daher trennt das Clustering die Wellenformen nicht. Für die Cityblock-Distanz ist die Trennung gut und die Wellenformenklassen werden wiederhergestellt. Schließlich trennt die Kosinus-Distanz Wellenform 1 und 2 überhaupt nicht, daher fasst das Clustering sie in denselben Cluster.

• 
• 
• 
• 
• 
• 
• 

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.patheffects as PathEffects
import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import pairwise_distances

np.random.seed(0)

# Generate waveform data
n_features = 2000
t = np.pi * np.linspace(0, 1, n_features)


def sqr(x):
    return np.sign(np.cos(x))


X = list()
y = list()
for i, (phi, a) in enumerate([(0.5, 0.15), (0.5, 0.6), (0.3, 0.2)]):
    for _ in range(30):
        phase_noise = 0.01 * np.random.normal()
        amplitude_noise = 0.04 * np.random.normal()
        additional_noise = 1 - 2 * np.random.rand(n_features)
        # Make the noise sparse
        additional_noise[np.abs(additional_noise) < 0.997] = 0

        X.append(
            12
            * (
                (a + amplitude_noise) * (sqr(6 * (t + phi + phase_noise)))
                + additional_noise
            )
        )
        y.append(i)

X = np.array(X)
y = np.array(y)

n_clusters = 3

labels = ("Waveform 1", "Waveform 2", "Waveform 3")

colors = ["#f7bd01", "#377eb8", "#f781bf"]

# Plot the ground-truth labelling
plt.figure()
plt.axes([0, 0, 1, 1])
for l, color, n in zip(range(n_clusters), colors, labels):
    lines = plt.plot(X[y == l].T, c=color, alpha=0.5)
    lines[0].set_label(n)

plt.legend(loc="best")

plt.axis("tight")
plt.axis("off")
plt.suptitle("Ground truth", size=20, y=1)


# Plot the distances
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    avg_dist = np.zeros((n_clusters, n_clusters))
    plt.figure(figsize=(5, 4.5))
    for i in range(n_clusters):
        for j in range(n_clusters):
            avg_dist[i, j] = pairwise_distances(
                X[y == i], X[y == j], metric=metric
            ).mean()
    avg_dist /= avg_dist.max()
    for i in range(n_clusters):
        for j in range(n_clusters):
            t = plt.text(
                i,
                j,
                "%5.3f" % avg_dist[i, j],
                verticalalignment="center",
                horizontalalignment="center",
            )
            t.set_path_effects(
                [PathEffects.withStroke(linewidth=5, foreground="w", alpha=0.5)]
            )

    plt.imshow(avg_dist, interpolation="nearest", cmap="cividis", vmin=0)
    plt.xticks(range(n_clusters), labels, rotation=45)
    plt.yticks(range(n_clusters), labels)
    plt.colorbar()
    plt.suptitle("Interclass %s distances" % metric, size=18, y=1)
    plt.tight_layout()


# Plot clustering results
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    model = AgglomerativeClustering(
        n_clusters=n_clusters, linkage="average", metric=metric
    )
    model.fit(X)
    plt.figure()
    plt.axes([0, 0, 1, 1])
    for l, color in zip(np.arange(model.n_clusters), colors):
        plt.plot(X[model.labels_ == l].T, c=color, alpha=0.5)
    plt.axis("tight")
    plt.axis("off")
    plt.suptitle("AgglomerativeClustering(metric=%s)" % metric, size=20, y=1)


plt.show()

Verwandte Beispiele

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

Eine Demo des strukturierten Ward Hierarchischen Clusterings auf einem Bild von Münzen

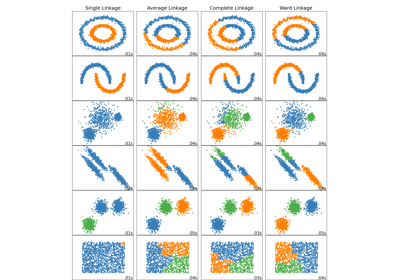
Vergleich verschiedener hierarchischer Linkage-Methoden auf Toy-Datensätzen

Vergleich verschiedener hierarchischer Linkage-Methoden auf Toy-Datensätzen

Hierarchisches Clustering mit und ohne Struktur

Hierarchisches Clustering mit und ohne Struktur

Auswahl der Anzahl von Clustern mit Silhouette-Analyse auf KMeans-Clustering

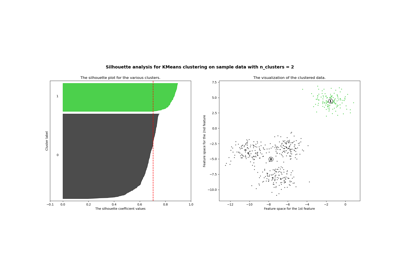
Auswahl der Anzahl von Clustern mit Silhouette-Analyse auf KMeans-Clustering