Monotone Einschränkungen

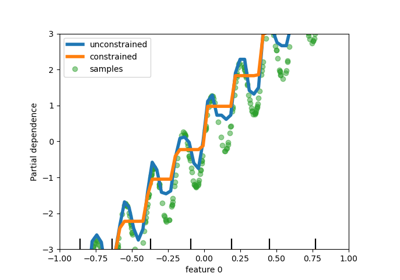
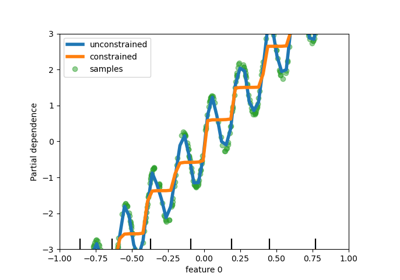
Dieses Beispiel veranschaulicht die Auswirkung von monotonen Einschränkungen auf einen Gradient Boosting-Schätzer.

Wir erstellen einen künstlichen Datensatz, bei dem der Zielwert im Allgemeinen positiv mit dem ersten Merkmal korreliert ist (mit einigen zufälligen und nicht zufälligen Variationen) und im Allgemeinen negativ mit dem zweiten Merkmal korreliert.

Durch das Erzwingen einer monotonen Zunahme oder Abnahme des Merkmals während des Lernprozesses ist der Schätzer in der Lage, dem allgemeinen Trend richtig zu folgen, anstatt den Variationen ausgesetzt zu sein.

Dieses Beispiel wurde von der XGBoost-Dokumentation inspiriert.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.inspection import PartialDependenceDisplay

rng = np.random.RandomState(0)

n_samples = 1000
f_0 = rng.rand(n_samples)
f_1 = rng.rand(n_samples)
X = np.c_[f_0, f_1]
noise = rng.normal(loc=0.0, scale=0.01, size=n_samples)

# y is positively correlated with f_0, and negatively correlated with f_1
y = 5 * f_0 + np.sin(10 * np.pi * f_0) - 5 * f_1 - np.cos(10 * np.pi * f_1) + noise

Passen Sie ein erstes Modell an diesen Datensatz ohne Einschränkungen an.

gbdt_no_cst = HistGradientBoostingRegressor()
gbdt_no_cst.fit(X, y)

HistGradientBoostingRegressor()

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Passen Sie ein zweites Modell an diesen Datensatz mit monotoner Zunahme (1) und monotoner Abnahme (-1) Einschränkungen an.

gbdt_with_monotonic_cst = HistGradientBoostingRegressor(monotonic_cst=[1, -1])
gbdt_with_monotonic_cst.fit(X, y)

HistGradientBoostingRegressor(monotonic_cst=[1, -1])

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Lassen Sie uns die partielle Abhängigkeit der Vorhersagen von den beiden Merkmalen anzeigen.

fig, ax = plt.subplots()
disp = PartialDependenceDisplay.from_estimator(
    gbdt_no_cst,
    X,
    features=[0, 1],
    feature_names=(
        "First feature",
        "Second feature",
    ),
    line_kw={"linewidth": 4, "label": "unconstrained", "color": "tab:blue"},
    ax=ax,
)
PartialDependenceDisplay.from_estimator(
    gbdt_with_monotonic_cst,
    X,
    features=[0, 1],
    line_kw={"linewidth": 4, "label": "constrained", "color": "tab:orange"},
    ax=disp.axes_,
)

for f_idx in (0, 1):
    disp.axes_[0, f_idx].plot(
        X[:, f_idx], y, "o", alpha=0.3, zorder=-1, color="tab:green"
    )
    disp.axes_[0, f_idx].set_ylim(-6, 6)

plt.legend()
fig.suptitle("Monotonic constraints effect on partial dependences")
plt.show()

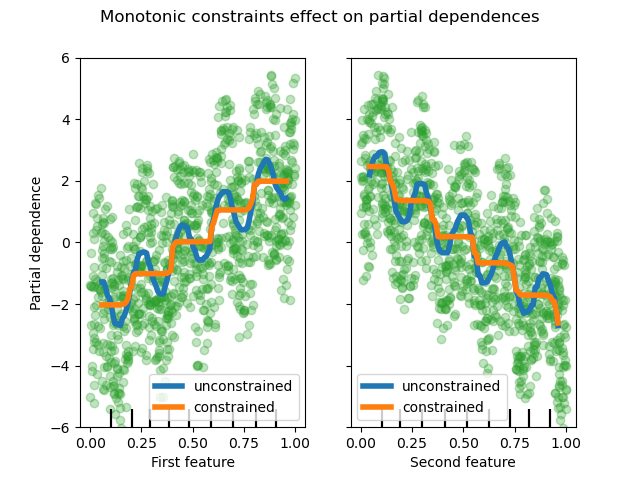
Wir können sehen, dass die Vorhersagen des nicht eingeschränkten Modells die Oszillationen der Daten erfassen, während das eingeschränkte Modell dem allgemeinen Trend folgt und die lokalen Variationen ignoriert.

Verwendung von Merkmalsnamen zur Angabe von monotonen Einschränkungen

Beachten Sie, dass, wenn die Trainingsdaten Merkmalsnamen haben, es möglich ist, die monotonen Einschränkungen durch Übergabe eines Wörterbuchs anzugeben.

import pandas as pd

X_df = pd.DataFrame(X, columns=["f_0", "f_1"])

gbdt_with_monotonic_cst_df = HistGradientBoostingRegressor(
    monotonic_cst={"f_0": 1, "f_1": -1}
).fit(X_df, y)

np.allclose(
    gbdt_with_monotonic_cst_df.predict(X_df), gbdt_with_monotonic_cst.predict(X)
)

True

Verwandte Beispiele

Release Highlights für scikit-learn 0.23

Release Highlights für scikit-learn 0.23

Release Highlights für scikit-learn 1.4

Release Highlights für scikit-learn 1.4

Merkmale in Histogram Gradient Boosting Bäumen

Merkmale in Histogram Gradient Boosting Bäumen

Fortgeschrittene Plotting mit Partial Dependence

Fortgeschrittene Plotting mit Partial Dependence