Scheitern des maschinellen Lernens bei der Inferenz kausaler Effekte

Modelle des maschinellen Lernens sind hervorragend geeignet, um statistische Zusammenhänge zu messen. Leider sind diese Modelle, es sei denn, wir sind bereit, starke Annahmen über die Daten zu treffen, nicht in der Lage, kausale Effekte zu schlussfolgern.

Um dies zu veranschaulichen, simulieren wir eine Situation, in der wir versuchen, eine der wichtigsten Fragen der Bildungsökonomie zu beantworten: was ist der kausale Effekt des Erwerbs eines Hochschulabschlusses auf den Stundenlohn? Obwohl die Antwort auf diese Frage für politische Entscheidungsträger entscheidend ist, verhindern verzerrte ausgelassene Variablen (OVB), dass wir diesen kausalen Effekt identifizieren können.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Der Datensatz: simulierte Stundenlöhne

Der Prozess der Datengenerierung ist im folgenden Code dargelegt. Berufserfahrung in Jahren und ein Maß für die Fähigkeit werden aus Normalverteilungen gezogen; der Stundenlohn eines der Elternteile wird aus einer Beta-Verteilung gezogen. Wir erstellen dann eine Indikatorvariable für den Hochschulabschluss, die positiv von der Fähigkeit und dem Stundenlohn der Eltern beeinflusst wird. Schließlich modellieren wir die Stundenlöhne als lineare Funktion aller vorherigen Variablen und einer Zufallskomponente. Beachten Sie, dass alle Variablen einen positiven Einfluss auf die Stundenlöhne haben.

import numpy as np
import pandas as pd

n_samples = 10_000
rng = np.random.RandomState(32)

experiences = rng.normal(20, 10, size=n_samples).astype(int)
experiences[experiences < 0] = 0
abilities = rng.normal(0, 0.15, size=n_samples)
parent_hourly_wages = 50 * rng.beta(2, 8, size=n_samples)
parent_hourly_wages[parent_hourly_wages < 0] = 0
college_degrees = (
    9 * abilities + 0.02 * parent_hourly_wages + rng.randn(n_samples) > 0.7
).astype(int)

true_coef = pd.Series(
    {
        "college degree": 2.0,
        "ability": 5.0,
        "experience": 0.2,
        "parent hourly wage": 1.0,
    }
)
hourly_wages = (
    true_coef["experience"] * experiences
    + true_coef["parent hourly wage"] * parent_hourly_wages
    + true_coef["college degree"] * college_degrees
    + true_coef["ability"] * abilities
    + rng.normal(0, 1, size=n_samples)
)

hourly_wages[hourly_wages < 0] = 0

Beschreibung der simulierten Daten

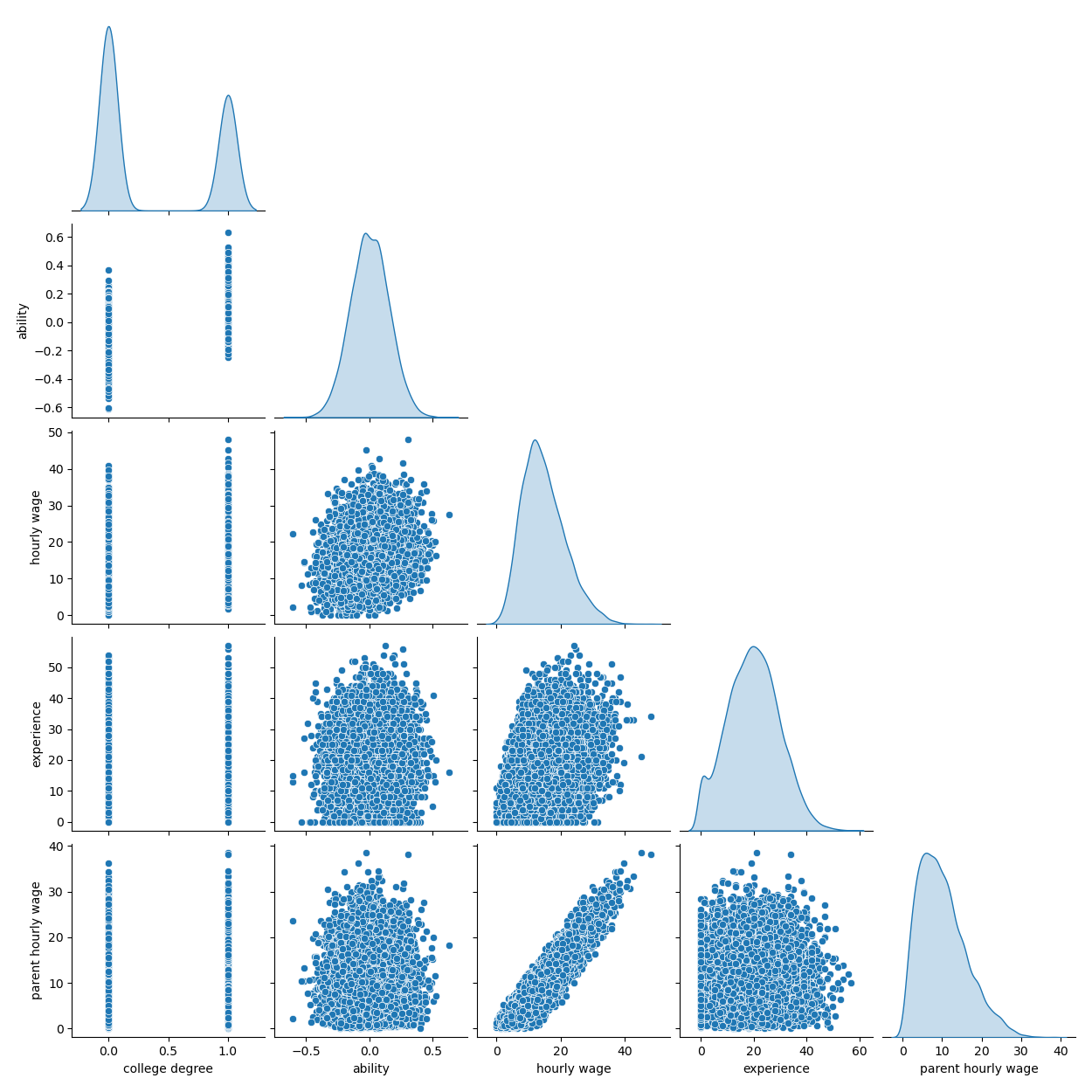
Das folgende Diagramm zeigt die Verteilung jeder Variablen und paarweise Streudiagramme. Entscheidend für unsere OVB-Geschichte ist die positive Beziehung zwischen Fähigkeit und Hochschulabschluss.

import seaborn as sns

df = pd.DataFrame(
    {
        "college degree": college_degrees,
        "ability": abilities,
        "hourly wage": hourly_wages,
        "experience": experiences,
        "parent hourly wage": parent_hourly_wages,
    }
)

grid = sns.pairplot(df, diag_kind="kde", corner=True)

Im nächsten Abschnitt trainieren wir Vorhersagemodelle und trennen daher die Zielspalte von den Merkmalen und teilen die Daten in ein Trainings- und ein Testset auf.

from sklearn.model_selection import train_test_split

target_name = "hourly wage"
X, y = df.drop(columns=target_name), df[target_name]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

Einkommensvorhersage mit vollständig beobachteten Variablen

Zunächst trainieren wir ein Vorhersagemodell, ein LinearRegression-Modell. In diesem Experiment gehen wir davon aus, dass alle Variablen, die vom wahren generativen Modell verwendet werden, verfügbar sind.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score

features_names = ["experience", "parent hourly wage", "college degree", "ability"]

regressor_with_ability = LinearRegression()
regressor_with_ability.fit(X_train[features_names], y_train)
y_pred_with_ability = regressor_with_ability.predict(X_test[features_names])
R2_with_ability = r2_score(y_test, y_pred_with_ability)

print(f"R2 score with ability: {R2_with_ability:.3f}")

R2 score with ability: 0.975

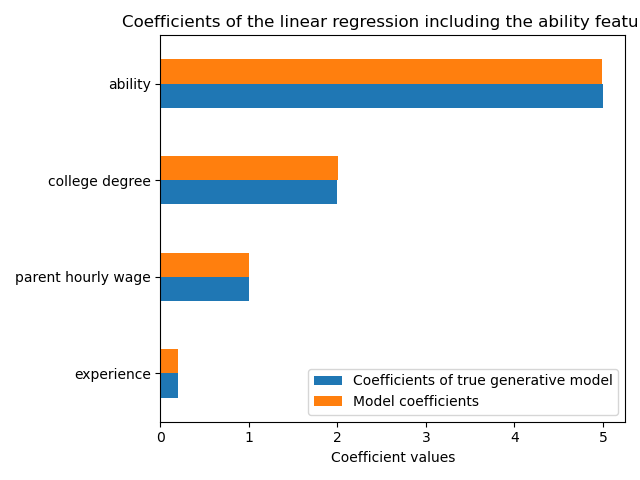
Dieses Modell sagt die Stundenlöhne gut voraus, wie der hohe R2-Score zeigt. Wir ploidie Modellkoeffizienten, um zu zeigen, dass wir die Werte des wahren generativen Modells exakt wiederherstellen.

import matplotlib.pyplot as plt

model_coef = pd.Series(regressor_with_ability.coef_, index=features_names)
coef = pd.concat(
    [true_coef[features_names], model_coef],
    keys=["Coefficients of true generative model", "Model coefficients"],
    axis=1,
)
ax = coef.plot.barh()
ax.set_xlabel("Coefficient values")
ax.set_title("Coefficients of the linear regression including the ability features")
_ = plt.tight_layout()

Einkommensvorhersage mit partiellen Beobachtungen

In der Praxis sind intellektuelle Fähigkeiten nicht beobachtbar oder werden nur anhand von Proxies geschätzt, die indirekt auch die Bildung messen (z. B. durch IQ-Tests). Das Weglassen des Merkmals "Fähigkeit" aus einem linearen Modell bläht die Schätzung durch eine positive OVB auf.

features_names = ["experience", "parent hourly wage", "college degree"]

regressor_without_ability = LinearRegression()
regressor_without_ability.fit(X_train[features_names], y_train)
y_pred_without_ability = regressor_without_ability.predict(X_test[features_names])
R2_without_ability = r2_score(y_test, y_pred_without_ability)

print(f"R2 score without ability: {R2_without_ability:.3f}")

R2 score without ability: 0.968

Die Vorhersagekraft unseres Modells ist in Bezug auf den R2-Score ähnlich, wenn wir das Merkmal "Fähigkeit" weglassen. Nun prüfen wir, ob die Koeffizienten des Modells von denen des wahren generativen Modells abweichen.

model_coef = pd.Series(regressor_without_ability.coef_, index=features_names)
coef = pd.concat(
    [true_coef[features_names], model_coef],
    keys=["Coefficients of true generative model", "Model coefficients"],
    axis=1,
)
ax = coef.plot.barh()
ax.set_xlabel("Coefficient values")
_ = ax.set_title("Coefficients of the linear regression excluding the ability feature")
plt.tight_layout()
plt.show()

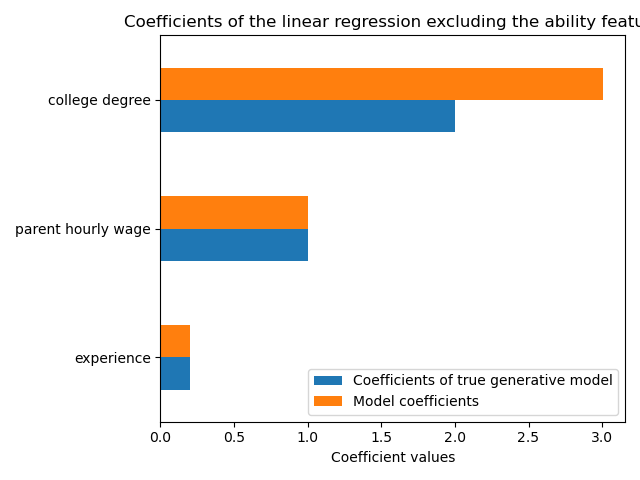
Um die ausgelassene Variable zu kompensieren, bläht das Modell den Koeffizienten des Merkmals "Hochschulabschluss" auf. Daher ist die Interpretation dieses Koeffizientenwerts als kausaler Effekt des wahren generativen Modells falsch.

Gewonnene Erkenntnisse

Modelle des maschinellen Lernens sind nicht für die Schätzung kausaler Effekte konzipiert. Obwohl wir dies mit einem linearen Modell gezeigt haben, kann OVB jeden Modelltyp beeinflussen.

Bei der Interpretation eines Koeffizienten oder einer Änderung der Vorhersagen, die durch eine Änderung eines der Merkmale hervorgerufen wird, ist es wichtig, potenziell unbeobachtete Variablen zu berücksichtigen, die sowohl mit dem fraglichen Merkmal als auch mit der Zielvariablen korreliert sein könnten. Solche Variablen werden als Confounding Variables bezeichnet. Um kausale Effekte trotz Störvariablen immer noch schätzen zu können, führen Forscher in der Regel Experimente durch, bei denen die Behandlungsvariable (z. B. Hochschulabschluss) randomisiert wird. Wenn ein Experiment unerschwinglich teuer oder unethisch ist, können Forscher manchmal andere kausale Inferenztechniken verwenden, wie z. B. Instrumental Variables (IV) Schätzungen.

Verwandte Beispiele

Häufige Fallstricke bei der Interpretation von Koeffizienten linearer Modelle

Häufige Fallstricke bei der Interpretation von Koeffizienten linearer Modelle

Nicht-negative kleinste Quadrate

Nicht-negative kleinste Quadrate

Ridge-Koeffizienten als Funktion der L2-Regularisierung

Ridge-Koeffizienten als Funktion der L2-Regularisierung

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Auswirkung der Modellregularisierung auf Trainings- und Testfehler