Feature-Importanzen mit einem Wald von Bäumen

Dieses Beispiel zeigt die Verwendung eines Waldes von Bäumen zur Bewertung der Bedeutung von Merkmalen bei einer künstlichen Klassifizierungsaufgabe. Die blauen Balken stellen die Feature-Importanzen des Waldes dar, zusammen mit ihrer Variabilität zwischen den Bäumen, die durch die Fehlerbalken repräsentiert wird.

Wie erwartet legt die Darstellung nahe, dass 3 Merkmale informativ sind, während die übrigen es nicht sind.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt

Datengenerierung und Modellfitting

Wir generieren einen synthetischen Datensatz mit nur 3 informativen Merkmalen. Wir werden den Datensatz explizit nicht mischen, um sicherzustellen, dass die informativen Merkmale den drei ersten Spalten von X entsprechen. Darüber hinaus werden wir unseren Datensatz in Trainings- und Testuntergruppen aufteilen.

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

X, y = make_classification(
    n_samples=1000,
    n_features=10,
    n_informative=3,
    n_redundant=0,
    n_repeated=0,
    n_classes=2,
    random_state=0,
    shuffle=False,
)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

Ein Random Forest-Klassifikator wird gefittet, um die Feature-Importanzen zu berechnen.

from sklearn.ensemble import RandomForestClassifier

feature_names = [f"feature {i}" for i in range(X.shape[1])]
forest = RandomForestClassifier(random_state=0)
forest.fit(X_train, y_train)

RandomForestClassifier(random_state=0)

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

Feature-Importanz basierend auf der mittleren Verringerung der Unreinheit

Feature-Importanzen werden durch das gefittete Attribut feature_importances_ bereitgestellt und als Mittelwert und Standardabweichung der Akkumulation der Unreinheitsverringerung innerhalb jedes Baumes berechnet.

Warnung

Unreinheitsbasierte Feature-Importanzen können bei **Merkmalen mit hoher Kardinalität** (viele eindeutige Werte) irreführend sein. Siehe Permutation Feature Importance als Alternative unten.

import time

import numpy as np

start_time = time.time()
importances = forest.feature_importances_
std = np.std([tree.feature_importances_ for tree in forest.estimators_], axis=0)
elapsed_time = time.time() - start_time

print(f"Elapsed time to compute the importances: {elapsed_time:.3f} seconds")

Elapsed time to compute the importances: 0.014 seconds

Lassen Sie uns die unreinheitsbasierte Bedeutung plotten.

import pandas as pd

forest_importances = pd.Series(importances, index=feature_names)

fig, ax = plt.subplots()
forest_importances.plot.bar(yerr=std, ax=ax)
ax.set_title("Feature importances using MDI")
ax.set_ylabel("Mean decrease in impurity")
fig.tight_layout()

Wir stellen fest, dass, wie erwartet, die ersten drei Merkmale als wichtig erachtet werden.

Feature-Importanz basierend auf Permutation von Merkmalen

Die Permutation Feature Importance überwindet Einschränkungen der unreinheitsbasierten Feature Importance: Sie hat keine Voreingenommenheit gegenüber Merkmalen mit hoher Kardinalität und kann auf einem links liegenden Testdatensatz berechnet werden.

from sklearn.inspection import permutation_importance

start_time = time.time()
result = permutation_importance(
    forest, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
elapsed_time = time.time() - start_time
print(f"Elapsed time to compute the importances: {elapsed_time:.3f} seconds")

forest_importances = pd.Series(result.importances_mean, index=feature_names)

Elapsed time to compute the importances: 0.906 seconds

Die Berechnung für die vollständige Permutations-Wichtigkeit ist aufwendiger. Jedes Merkmal wird n Mal gemischt und das Modell wird verwendet, um Vorhersagen auf den permutierten Daten zu treffen, um den Leistungsabfall zu sehen. Weitere Einzelheiten finden Sie unter Permutation Feature Importance. Wir können nun das Ranking der Wichtigkeit plotten.

fig, ax = plt.subplots()
forest_importances.plot.bar(yerr=result.importances_std, ax=ax)
ax.set_title("Feature importances using permutation on full model")
ax.set_ylabel("Mean accuracy decrease")
fig.tight_layout()
plt.show()

Dieselbe Merkmale werden mit beiden Methoden als am wichtigsten erkannt. Obwohl sich die relativen Bedeutungen unterscheiden. Wie in den Plots zu sehen ist, ist MDI weniger wahrscheinlich als die Permutations-Wichtigkeit, ein Merkmal vollständig auszulassen.

Verwandte Beispiele

Permutations-Wichtigkeit vs. Random Forest Merkmals-Wichtigkeit (MDI)

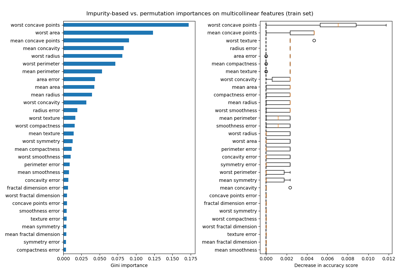
Permutations-Wichtigkeit vs. Random Forest Merkmals-Wichtigkeit (MDI)

Permutations-Wichtigkeit bei multikollinearen oder korrelierten Merkmalen

Permutations-Wichtigkeit bei multikollinearen oder korrelierten Merkmalen

Gradient Boosting Regression

Gradient Boosting Regression

Release Highlights für scikit-learn 0.22

Release Highlights für scikit-learn 0.22