5.2. Permutation Feature Importance#
Permutation Feature Importance ist eine Technik zur Modellinspektion, die den Beitrag jedes Merkmals zur statistischen Leistung eines angepassten Modells auf einem gegebenen tabellarischen Datensatz misst. Diese Technik ist besonders nützlich für nichtlineare oder undurchsichtige Schätzer und beinhaltet das zufällige Mischen der Werte eines einzelnen Merkmals und die Beobachtung des daraus resultierenden Abfalls des Modellscores [1]. Indem die Beziehung zwischen dem Merkmal und dem Ziel unterbrochen wird, ermitteln wir, wie stark sich das Modell auf ein bestimmtes Merkmal verlässt.
In den folgenden Abbildungen beobachten wir den Effekt der Permutation von Merkmalen auf die Korrelation zwischen dem Merkmal und dem Ziel und folglich auf die statistische Leistung des Modells.
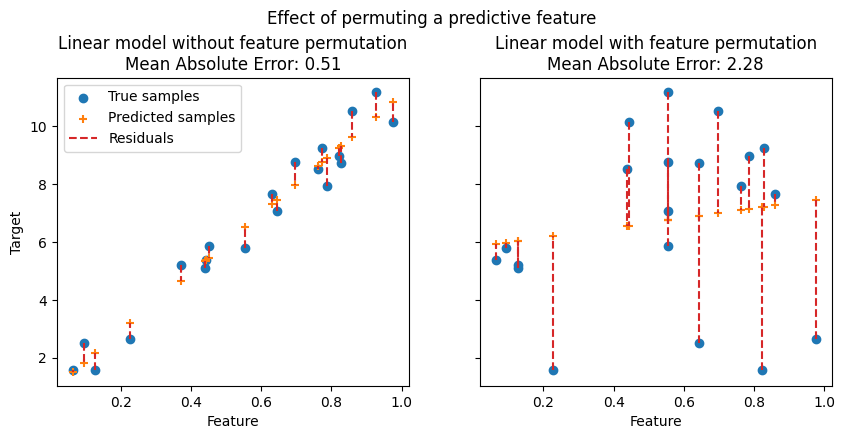
In der oberen Abbildung beobachten wir, dass die Permutation eines prädiktiven Merkmals die Korrelation zwischen dem Merkmal und dem Ziel unterbricht und folglich die statistische Leistung des Modells abnimmt. In der unteren Abbildung beobachten wir, dass die Permutation eines nicht-prädiktiven Merkmals die statistische Leistung des Modells nicht wesentlich verschlechtert.
Ein wesentlicher Vorteil der Permutation Feature Importance ist, dass sie modellunabhängig ist, d.h. sie kann auf jeden angepassten Schätzer angewendet werden. Darüber hinaus kann sie mehrmals mit unterschiedlichen Permutationen des Merkmals berechnet werden, was ein Maß für die Varianz der geschätzten Merkmalswichtigkeiten für das spezifisch trainierte Modell liefert.
Die folgende Abbildung zeigt die Permutation Feature Importance eines auf einer erweiterten Version des Titanic-Datensatzes trainierten RandomForestClassifier, der ein Merkmal random_cat und ein Merkmal random_num enthält, d.h. ein kategoriales und ein numerisches Merkmal, die in keiner Weise mit der Zielvariablen korreliert sind.
Warnung
Merkmale, die für ein **schlechtes Modell** (niedriger Cross-Validation-Score) als **wenig wichtig** eingestuft werden, könnten für ein **gutes Modell** als **sehr wichtig** gelten. Daher ist es immer wichtig, die Vorhersagekraft eines Modells anhand eines zurückgehaltenen Datensatzes (oder besser noch mit Cross-Validation) zu bewerten, bevor die Wichtigkeiten berechnet werden. Permutation Importance spiegelt nicht den intrinsischen Vorhersagewert eines Merkmals an sich wider, sondern **wie wichtig dieses Merkmal für ein bestimmtes Modell ist**.
Die Funktion permutation_importance berechnet die Merkmalswichtigkeit von Schätzern für einen gegebenen Datensatz. Der Parameter n_repeats legt fest, wie oft ein Merkmal zufällig gemischt wird, und gibt eine Stichprobe von Merkmalswichtigkeiten zurück.
Betrachten wir das folgende trainierte Regressionsmodell
>>> from sklearn.datasets import load_diabetes
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import Ridge
>>> diabetes = load_diabetes()
>>> X_train, X_val, y_train, y_val = train_test_split(
... diabetes.data, diabetes.target, random_state=0)
...
>>> model = Ridge(alpha=1e-2).fit(X_train, y_train)
>>> model.score(X_val, y_val)
0.356...
Seine Validierungsleistung, gemessen am \(R^2\)-Score, ist signifikant größer als das Zufallsniveau. Dies ermöglicht die Verwendung der Funktion permutation_importance, um zu untersuchen, welche Merkmale am prädiktivsten sind.
>>> from sklearn.inspection import permutation_importance
>>> r = permutation_importance(model, X_val, y_val,
... n_repeats=30,
... random_state=0)
...
>>> for i in r.importances_mean.argsort()[::-1]:
... if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
... print(f"{diabetes.feature_names[i]:<8}"
... f"{r.importances_mean[i]:.3f}"
... f" +/- {r.importances_std[i]:.3f}")
...
s5 0.204 +/- 0.050
bmi 0.176 +/- 0.048
bp 0.088 +/- 0.033
sex 0.056 +/- 0.023
Beachten Sie, dass die Wichtigkeitswerte für die Top-Merkmale einen großen Teil des Referenzscores von 0,356 darstellen.
Permutation Importances können entweder auf dem Trainingsdatensatz oder auf einem zurückgehaltenen Test- oder Validierungsdatensatz berechnet werden. Die Verwendung eines zurückgehaltenen Datensatzes macht es möglich, hervorzuheben, welche Merkmale am meisten zur Generalisierungsfähigkeit des inspizierten Modells beitragen. Merkmale, die auf dem Trainingsdatensatz wichtig sind, aber nicht auf dem zurückgehaltenen Datensatz, können dazu führen, dass das Modell überanpasst.
Die Permutation Feature Importance hängt von der mit dem Argument scoring angegebenen Score-Funktion ab. Dieses Argument akzeptiert mehrere Scorers, was rechnerisch effizienter ist, als permutation_importance mehrmals mit einem anderen Scorer nacheinander aufzurufen, da Modellvorhersagen wiederverwendet werden.
Beispiel für Permutation Feature Importance mit mehreren Scorers#
Im folgenden Beispiel verwenden wir eine Liste von Metriken, aber auch andere Eingabeformate sind möglich, wie in Verwendung von Mehrfachmetrik-Auswertungen dokumentiert.
>>> scoring = ['r2', 'neg_mean_absolute_percentage_error', 'neg_mean_squared_error']
>>> r_multi = permutation_importance(
... model, X_val, y_val, n_repeats=30, random_state=0, scoring=scoring)
...
>>> for metric in r_multi:
... print(f"{metric}")
... r = r_multi[metric]
... for i in r.importances_mean.argsort()[::-1]:
... if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
... print(f" {diabetes.feature_names[i]:<8}"
... f"{r.importances_mean[i]:.3f}"
... f" +/- {r.importances_std[i]:.3f}")
...
r2
s5 0.204 +/- 0.050
bmi 0.176 +/- 0.048
bp 0.088 +/- 0.033
sex 0.056 +/- 0.023
neg_mean_absolute_percentage_error
s5 0.081 +/- 0.020
bmi 0.064 +/- 0.015
bp 0.029 +/- 0.010
neg_mean_squared_error
s5 1013.866 +/- 246.445
bmi 872.726 +/- 240.298
bp 438.663 +/- 163.022
sex 277.376 +/- 115.123
Das Ranking der Merkmale ist für verschiedene Metriken ungefähr gleich, auch wenn die Skalen der Wichtigkeitswerte sehr unterschiedlich sind. Dies ist jedoch nicht garantiert und verschiedene Metriken können zu signifikant unterschiedlichen Merkmalswichtigkeiten führen, insbesondere bei Modellen, die für unausgewogene Klassifizierungsprobleme trainiert wurden, für die **die Wahl der Klassifizierungsmetrik entscheidend sein kann**.
5.2.1. Überblick über den Permutation Importance Algorithmus#
Eingaben: Angepasstes prädiktives Modell \(m\), tabellarischer Datensatz (Trainings- oder Validierungsdatensatz) \(D\).
Berechnen Sie den Referenzscore \(s\) des Modells \(m\) auf den Daten \(D\) (z. B. die Genauigkeit für einen Klassifikator oder \(R^2\) für einen Regressor).
Für jedes Merkmal \(j\) (Spalte von \(D\))
Für jede Wiederholung \(k\) in \({1, ..., K}\)
Mischen Sie zufällig die Spalte \(j\) des Datensatzes \(D\), um eine korrumpierte Version der Daten namens \(\tilde{D}_{k,j}\) zu erzeugen.
Berechnen Sie den Score \(s_{k,j}\) des Modells \(m\) auf den korrumpierten Daten \(\tilde{D}_{k,j}\).
Berechnen Sie die Wichtigkeit \(i_j\) für das Merkmal \(f_j\), definiert als
\[i_j = s - \frac{1}{K} \sum_{k=1}^{K} s_{k,j}\]
5.2.2. Beziehung zur verunreinigungsbasierten Wichtigkeit bei Bäumen#
Baumbasierte Modelle bieten ein alternatives Maß für die Merkmalswichtigkeiten, basierend auf der mittleren Verringerung der Verunreinigung (MDI). Die Verunreinigung wird durch das Teilungskriterium der Entscheidungsbäume quantifiziert (Gini, Log Loss oder Mean Squared Error). Diese Methode kann jedoch Merkmalen, die auf ungesehenen Daten möglicherweise nicht prädiktiv sind, eine hohe Wichtigkeit zuweisen, wenn das Modell überanpasst ist. Permutationsbasierte Merkmalswichtigkeit vermeidet dieses Problem, da sie auf ungesehenen Daten berechnet werden kann.
Darüber hinaus ist die verunreinigungsbasierte Merkmalswichtigkeit für Bäume **stark verzerrt** und **begünstigt Merkmale mit hoher Kardinalität** (typischerweise numerische Merkmale) gegenüber Merkmalen mit geringer Kardinalität wie binären Merkmalen oder kategorialen Variablen mit einer kleinen Anzahl möglicher Kategorien.
Permutationsbasierte Merkmalswichtigkeiten weisen eine solche Verzerrung nicht auf. Darüber hinaus kann die Permutation Feature Importance mit jeder beliebigen Leistungskennzahl anhand der Modellvorhersagen berechnet und zur Analyse jeder Modellklasse (nicht nur baumbasierter Modelle) verwendet werden.
Das folgende Beispiel hebt die Einschränkungen der verunreinigungsbasierten Merkmalswichtigkeit im Gegensatz zur permutationsbasierten Merkmalswichtigkeit hervor: Permutation Importance vs. Random Forest Feature Importance (MDI).
5.2.3. Irreführende Werte bei stark korrelierten Merkmalen#
Wenn zwei Merkmale korreliert sind und eines der Merkmale permutiert wird, hat das Modell über sein korreliertes Merkmal immer noch Zugriff auf letzteres. Dies führt zu einem niedrigeren gemeldeten Wichtigkeitswert für beide Merkmale, obwohl sie *tatsächlich* wichtig sein könnten.
Die folgende Abbildung zeigt die Permutation Feature Importance eines RandomForestClassifier, der unter Verwendung des Brustkrebs Wisconsin (diagnostischer) Datensatz trainiert wurde, der stark korrelierte Merkmale enthält. Eine naive Interpretation würde darauf hindeuten, dass alle Merkmale unwichtig sind.
Eine Möglichkeit, das Problem zu lösen, ist das Clustering von korrelierten Merkmalen und die Beibehaltung nur eines Merkmals aus jedem Cluster.
Weitere Details zu einer solchen Strategie finden Sie im Beispiel Permutation Importance mit multikollinearen oder korrelierten Merkmalen.
Beispiele
Permutations-Wichtigkeit vs. Random Forest Merkmals-Wichtigkeit (MDI)
Permutations-Wichtigkeit bei multikollinearen oder korrelierten Merkmalen
Referenzen