2.9. Neuronale Netzwerkmodelle (unüberwacht)#

2.9.1. Restricted Boltzmann Machines#

Restricted Boltzmann Machines (RBMs) sind unüberwachte nichtlineare Merkmalslerner, die auf einem probabilistischen Modell basieren. Die von einer RBM oder einer Hierarchie von RBMs extrahierten Merkmale ergeben oft gute Ergebnisse, wenn sie in einen linearen Klassifikator wie eine lineare SVM oder ein Perzeptron eingespeist werden.

Das Modell macht Annahmen über die Verteilung der Eingaben. Derzeit bietet scikit-learn nur BernoulliRBM an, das annimmt, dass die Eingaben entweder binäre Werte sind oder Werte zwischen 0 und 1, wobei jeder Wert die Wahrscheinlichkeit kodiert, dass das spezifische Merkmal aktiviert wird.

Die RBM versucht, die Likelihood der Daten mithilfe eines bestimmten grafischen Modells zu maximieren. Der verwendete Parameterlernalgorithmus (Stochastic Maximum Likelihood) verhindert, dass die Repräsentationen weit von den Eingabedaten abweichen, was dazu führt, dass sie interessante Regelmäßigkeiten erfassen, aber das Modell für kleine Datensätze weniger nützlich macht und für die Dichteschätzung normalerweise nicht brauchbar ist.

Die Methode gewann an Popularität für die Initialisierung tiefer neuronaler Netze mit den Gewichten unabhängiger RBMs. Diese Methode ist als unüberwachtes Pre-Training bekannt.

../_images/sphx_glr_plot_rbm_logistic_classification_001.png

Beispiele

2.9.1.1. Grafisches Modell und Parametrisierung#

Das grafische Modell einer RBM ist ein vollständig verbundenes bipartites Diagramm.

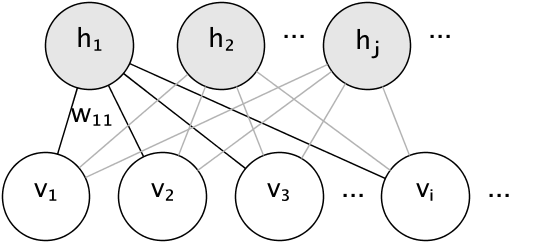
../_images/rbm_graph.png

Die Knoten sind Zufallsvariablen, deren Zustände vom Zustand der anderen verbundenen Knoten abhängen. Das Modell wird daher durch die Gewichte der Verbindungen sowie einen Achsenabschnittsterm (Bias) für jede sichtbare und versteckte Einheit parametrisiert, der der Einfachheit halber in der Abbildung weggelassen wurde.

Die Energiefunktion misst die Qualität einer gemeinsamen Zuweisung

\[E(\mathbf{v}, \mathbf{h}) = -\sum_i \sum_j w_{ij}v_ih_j - \sum_i b_iv_i - \sum_j c_jh_j\]

In der obigen Formel sind \(\mathbf{b}\) und \(\mathbf{c}\) die Achsenabschnittsvektoren für die sichtbaren und versteckten Schichten. Die gemeinsame Wahrscheinlichkeit des Modells wird anhand der Energie definiert

\[P(\mathbf{v}, \mathbf{h}) = \frac{e^{-E(\mathbf{v}, \mathbf{h})}}{Z}\]

Das Wort restricted (beschränkt) bezieht sich auf die bipartite Struktur des Modells, die eine direkte Interaktion zwischen versteckten Einheiten oder zwischen sichtbaren Einheiten verbietet. Das bedeutet, dass folgende bedingte Unabhängigkeiten angenommen werden:

\[\begin{split}h_i \bot h_j | \mathbf{v} \\ v_i \bot v_j | \mathbf{h}\end{split}\]

Die bipartite Struktur ermöglicht die Verwendung eines effizienten Block-Gibbs-Samplings für die Inferenz.

2.9.1.2. Bernoulli Restricted Boltzmann Machines#

Bei der BernoulliRBM sind alle Einheiten binäre stochastische Einheiten. Das bedeutet, dass die Eingabedaten entweder binär oder reellwertig zwischen 0 und 1 sein sollten, was die Wahrscheinlichkeit angibt, dass die sichtbare Einheit ein- oder ausgeschaltet wird. Dies ist ein gutes Modell für die Zeichenerkennung, bei der es darum geht, welche Pixel aktiv und welche nicht sind. Für Bilder von natürlichen Szenen passt es aufgrund des Hintergrunds, der Tiefe und der Tendenz benachbarter Pixel, gleiche Werte anzunehmen, nicht mehr.

Die bedingte Wahrscheinlichkeitsverteilung jeder Einheit wird durch die logistische Sigmoid-Aktivierungsfunktion der erhaltenen Eingabe gegeben:

\[\begin{split}P(v_i=1|\mathbf{h}) = \sigma(\sum_j w_{ij}h_j + b_i) \\ P(h_i=1|\mathbf{v}) = \sigma(\sum_i w_{ij}v_i + c_j)\end{split}\]

wobei \(\sigma\) die logistische Sigmoid-Funktion ist

\[\sigma(x) = \frac{1}{1 + e^{-x}}\]

2.9.1.3. Stochastic Maximum Likelihood Training#

Der in BernoulliRBM implementierte Trainingsalgorithmus ist als Stochastic Maximum Likelihood (SML) oder Persistent Contrastive Divergence (PCD) bekannt. Die direkte Optimierung der maximalen Likelihood ist aufgrund der Form der Daten-Likelihood nicht durchführbar:

\[\log P(v) = \log \sum_h e^{-E(v, h)} - \log \sum_{x, y} e^{-E(x, y)}\]

Zur Vereinfachung ist die obige Gleichung für ein einzelnes Trainingsbeispiel geschrieben. Der Gradient in Bezug auf die Gewichte besteht aus zwei Termen, die den obigen entsprechen. Sie werden aufgrund ihrer Vorzeichen üblicherweise als positiver Gradient und negativer Gradient bezeichnet. In dieser Implementierung werden die Gradienten über Mini-Batches von Stichproben geschätzt.

Bei der Maximierung der Log-Likelihood veranlasst der positive Gradient das Modell, verborgene Zustände zu bevorzugen, die mit den beobachteten Trainingsdaten kompatibel sind. Aufgrund der bipartiten Struktur von RBMs kann dies effizient berechnet werden. Der negative Gradient ist jedoch nicht bestimmbar. Sein Ziel ist es, die Energie von gemeinsamen Zuständen zu senken, die das Modell bevorzugt, und es dadurch bei den Daten zu halten. Dies kann durch Markov-Ketten-Monte-Carlo mit Block-Gibbs-Sampling approximiert werden, indem nacheinander jede der \(v\) und \(h\) gegeben die andere gesampelt wird, bis die Kette gemischt ist. Auf diese Weise generierte Stichproben werden manchmal als Fantasiepartikel bezeichnet. Dies ist ineffizient und es ist schwierig zu bestimmen, ob die Markov-Kette mischt.

Die Contrastive Divergence-Methode schlägt vor, die Kette nach einer geringen Anzahl von Iterationen, \(k\), üblicherweise sogar 1, zu stoppen. Diese Methode ist schnell und hat eine geringe Varianz, aber die Stichproben sind weit von der Modellverteilung entfernt.

Persistent Contrastive Divergence adressiert dies. Anstatt jedes Mal eine neue Kette zu starten, wenn der Gradient benötigt wird, und nur einen Gibbs-Sampling-Schritt durchzuführen, halten wir bei PCD eine Anzahl von Ketten (Fantasiepartikel), die nach jeder Gewichtsaktualisierung \(k\) Gibbs-Schritte ausgeführt werden. Dies ermöglicht den Partikeln, den Raum gründlicher zu erkunden.

Referenzen