1.7. Gauß-Prozesse#
Gauß-Prozesse (GP) sind eine nichtparametrische überwachte Lernmethode, die zur Lösung von Regressions- und probabilistischen Klassifikationsproblemen verwendet wird.
Die Vorteile von Gauß-Prozessen sind:
Die Vorhersage interpoliert die Beobachtungen (zumindest für reguläre Kerne).
Die Vorhersage ist probabilistisch (Gaußsch), sodass man empirische Konfidenzintervalle berechnen und basierend darauf entscheiden kann, ob die Vorhersage in einem bestimmten Interessengebiet neu angepasst (Online-Fitting, adaptives Fitting) werden sollte.
Vielseitig: Es können unterschiedliche Kerne spezifiziert werden. Gängige Kerne werden bereitgestellt, aber es ist auch möglich, benutzerdefinierte Kerne anzugeben.
Die Nachteile von Gauß-Prozessen sind:
Unsere Implementierung ist nicht sparsam, d.h. sie verwendet die gesamten Stichproben-/Merkmalsinformationen zur Durchführung der Vorhersage.
Sie verlieren an Effizienz in hochdimensionalen Räumen – insbesondere wenn die Anzahl der Merkmale einige Dutzend überschreitet.
1.7.1. Gauß-Prozess-Regression (GPR)#
Die GaussianProcessRegressor implementiert Gauß-Prozesse (GP) für Regressionszwecke. Hierfür muss der Prior des GP spezifiziert werden. Der GP kombiniert diesen Prior und die Likelihood-Funktion basierend auf Trainingsstichproben. Er ermöglicht einen probabilistischen Ansatz zur Vorhersage, indem er Mittelwert und Standardabweichung als Ausgabe bei der Vorhersage liefert.
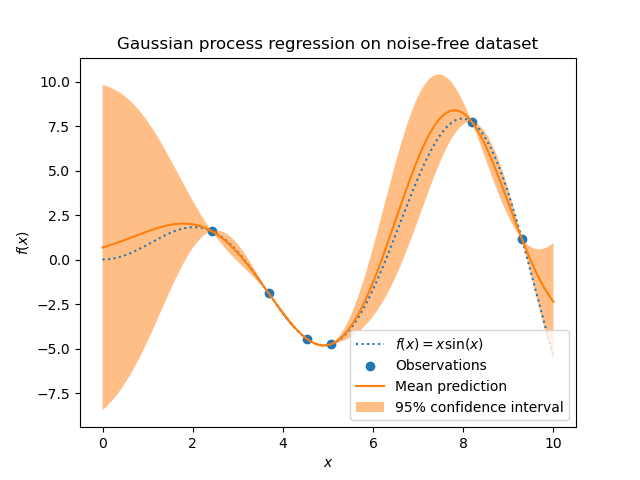
Der Prior-Mittelwert wird als konstant und Null (für normalize_y=False) oder als Mittelwert der Trainingsdaten (für normalize_y=True) angenommen. Die Kovarianz des Priors wird durch Übergabe eines Kernel-Objekts spezifiziert. Die Hyperparameter des Kernels werden beim Training der GaussianProcessRegressor optimiert, indem die Log-Marginal-Likelihood (LML) basierend auf dem übergebenen optimizer maximiert wird. Da die LML mehrere lokale Optima haben kann, kann der Optimizer wiederholt gestartet werden, indem n_restarts_optimizer spezifiziert wird. Der erste Durchlauf erfolgt immer ausgehend von den anfänglichen Hyperparameterwerten des Kernels; nachfolgende Durchläufe erfolgen ausgehend von Hyperparameterwerten, die zufällig aus dem Bereich der zulässigen Werte gewählt wurden. Wenn die anfänglichen Hyperparameter fixiert bleiben sollen, kann None als Optimizer übergeben werden.
Das Rauschlevel in den Zielwerten kann durch Übergabe über den Parameter alpha spezifiziert werden, entweder global als Skalar oder pro Datenpunkt. Beachten Sie, dass ein moderates Rauschlevel auch bei numerischen Instabilitäten während des Trainings hilfreich sein kann, da es effektiv als Tikhonov-Regularisierung implementiert wird, d.h. indem es zur Diagonalen der Kernel-Matrix addiert wird. Eine Alternative zur expliziten Angabe des Rauschlevels ist die Einbeziehung einer WhiteKernel-Komponente in den Kernel, die das globale Rauschlevel aus den Daten schätzen kann (siehe Beispiel unten). Die folgende Abbildung zeigt die Auswirkung von verrauschten Zielwerten bei Einstellung des Parameters alpha.
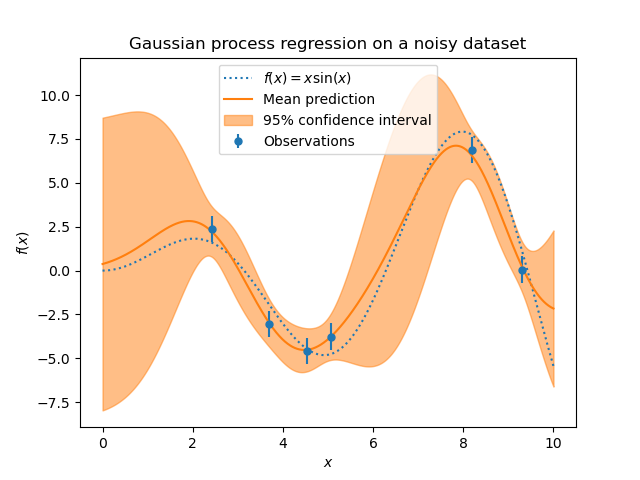
Die Implementierung basiert auf Algorithmus 2.1 von [RW2006]. Zusätzlich zur API von Standard-Scikit-learn-Estimators bietet GaussianProcessRegressor:
die Vorhersage ohne vorheriges Training (basierend auf dem GP-Prior)
eine zusätzliche Methode
sample_y(X), die Stichproben aus dem GPR (Prior oder Posterior) an gegebenen Eingaben auswerteteine Methode
log_marginal_likelihood(theta), die extern für andere Methoden zur Auswahl von Hyperparametern, z. B. mittels Markov-Chain-Monte-Carlo, verwendet werden kann.
Beispiele
1.7.2. Gauß-Prozess-Klassifikation (GPC)#
Die GaussianProcessClassifier implementiert Gauß-Prozesse (GP) für Klassifikationszwecke, genauer gesagt für probabilistische Klassifikation, bei der Testvorhersagen die Form von Klassenwahrscheinlichkeiten annehmen. GaussianProcessClassifier legt einen GP-Prior auf eine latente Funktion \(f\), die dann durch eine Link-Funktion \(\pi\) gequetscht wird, um die probabilistische Klassifikation zu erhalten. Die latente Funktion \(f\) ist eine sogenannte Störfunktion, deren Werte nicht beobachtet werden und für sich allein nicht relevant sind. Ihr Zweck ist es, eine bequeme Formulierung des Modells zu ermöglichen, und \(f\) wird bei der Vorhersage (integriert) eliminiert. GaussianProcessClassifier implementiert die logistische Link-Funktion, für die das Integral analytisch nicht berechnet werden kann, aber im Binärfall leicht angenähert wird.
Im Gegensatz zum Regressionssetting ist der Posterior der latenten Funktion \(f\) auch bei einem GP-Prior nicht Gaußsch, da eine Gaußsche Likelihood für diskrete Klassenlabels ungeeignet ist. Stattdessen wird eine nicht-Gaußsche Likelihood verwendet, die der logistischen Link-Funktion (Logit) entspricht. GaussianProcessClassifier approximiert den nicht-Gaußschen Posterior mithilfe einer Laplace-Approximation durch einen Gaußschen. Weitere Details finden Sie in Kapitel 3 von [RW2006].
Der GP-Prior-Mittelwert wird als Null angenommen. Die Kovarianz des Priors wird durch Übergabe eines Kernel-Objekts spezifiziert. Die Hyperparameter des Kernels werden während des Trainings von GaussianProcessRegressor optimiert, indem die Log-Marginal-Likelihood (LML) basierend auf dem übergebenen optimizer maximiert wird. Da die LML mehrere lokale Optima haben kann, kann der Optimizer wiederholt gestartet werden, indem n_restarts_optimizer spezifiziert wird. Der erste Durchlauf erfolgt immer ausgehend von den anfänglichen Hyperparameterwerten des Kernels; nachfolgende Durchläufe erfolgen ausgehend von Hyperparameterwerten, die zufällig aus dem Bereich der zulässigen Werte gewählt wurden. Wenn die anfänglichen Hyperparameter fixiert bleiben sollen, kann None als Optimizer übergeben werden.
In einigen Szenarien sind Informationen über die latente Funktion \(f\) gewünscht (d.h. der Mittelwert \(\bar{f_*}\) und die Varianz \(\text{Var}[f_*]\) beschrieben in den Gleichungen (3.21) und (3.24) von [RW2006]). Der GaussianProcessClassifier bietet über die Methode latent_mean_and_variance Zugriff auf diese Größen.
GaussianProcessClassifier unterstützt die Multiklassen-Klassifikation, indem er entweder One-vs-Rest- oder One-vs-One-basiertes Training und Vorhersage durchführt. Bei One-vs-Rest wird für jede Klasse ein binärer Gauß-Prozess-Klassifikator trainiert, der darauf trainiert ist, diese Klasse von den anderen zu trennen. Bei "one_vs_one" wird für jedes Paar von Klassen ein binärer Gauß-Prozess-Klassifikator trainiert, der darauf trainiert ist, diese beiden Klassen zu trennen. Die Vorhersagen dieser binären Prädiktoren werden zu Multiklassen-Vorhersagen kombiniert. Siehe den Abschnitt über Multiklassen-Klassifikation für weitere Details.
Im Falle der Gauß-Prozess-Klassifikation kann "one_vs_one" rechnerisch günstiger sein, da es viele Probleme mit nur einem Teil des gesamten Trainingsdatensatzes lösen muss, anstatt weniger Probleme auf dem gesamten Datensatz. Da die Gauß-Prozess-Klassifikation kubisch mit der Größe des Datensatzes skaliert, kann dies erheblich schneller sein. Beachten Sie jedoch, dass "one_vs_one" keine Wahrscheinlichkeitsschätzungen, sondern nur einfache Vorhersagen unterstützt. Darüber hinaus ist zu beachten, dass GaussianProcessClassifier keine echte Multiklassen-Laplace-Approximation intern implementiert (noch), sondern, wie oben diskutiert, auf der Lösung mehrerer interner binärer Klassifikationsaufgaben basiert, die mittels One-vs-Rest oder One-vs-One kombiniert werden.
1.7.3. GPC-Beispiele#
1.7.3.1. Probabilistische Vorhersagen mit GPC#
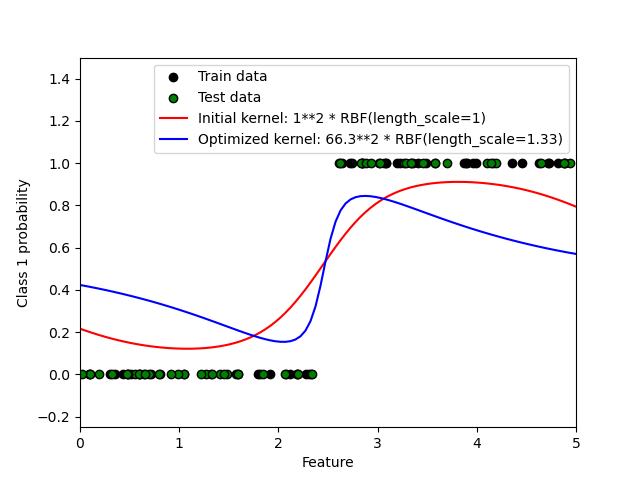
Dieses Beispiel illustriert die vorhergesagte Wahrscheinlichkeit von GPC für einen RBF-Kernel mit verschiedenen Wahlmöglichkeiten für die Hyperparameter. Die erste Abbildung zeigt die vorhergesagte Wahrscheinlichkeit von GPC mit willkürlich gewählten Hyperparametern und mit den Hyperparametern, die der maximalen Log-Marginal-Likelihood (LML) entsprechen.
Während die durch Optimierung der LML gewählten Hyperparameter eine erheblich größere LML aufweisen, schneiden sie beim Log-Loss auf Testdaten etwas schlechter ab. Die Abbildung zeigt, dass dies daran liegt, dass sie eine steile Änderung der Klassenwahrscheinlichkeiten an den Klassengrenzen aufweisen (was gut ist), aber vorhergesagte Wahrscheinlichkeiten nahe 0,5 weit entfernt von den Klassengrenzen haben (was schlecht ist). Dieser unerwünschte Effekt wird durch die intern von GPC verwendete Laplace-Approximation verursacht.
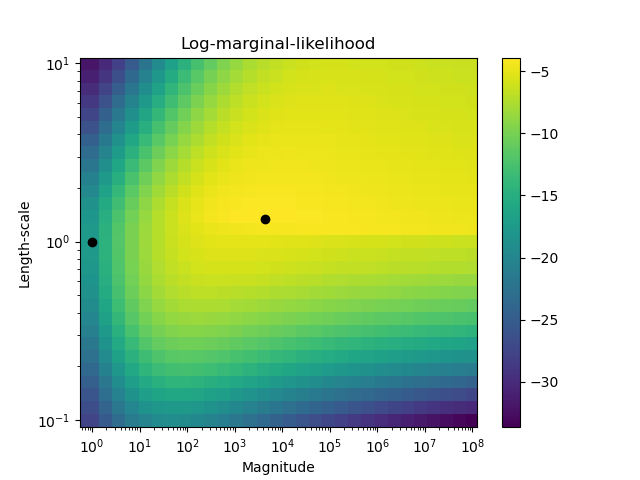
Die zweite Abbildung zeigt die Log-Marginal-Likelihood für verschiedene Wahlmöglichkeiten der Hyperparameter des Kernels, wobei die beiden Wahlmöglichkeiten der Hyperparameter aus der ersten Abbildung durch schwarze Punkte hervorgehoben werden.
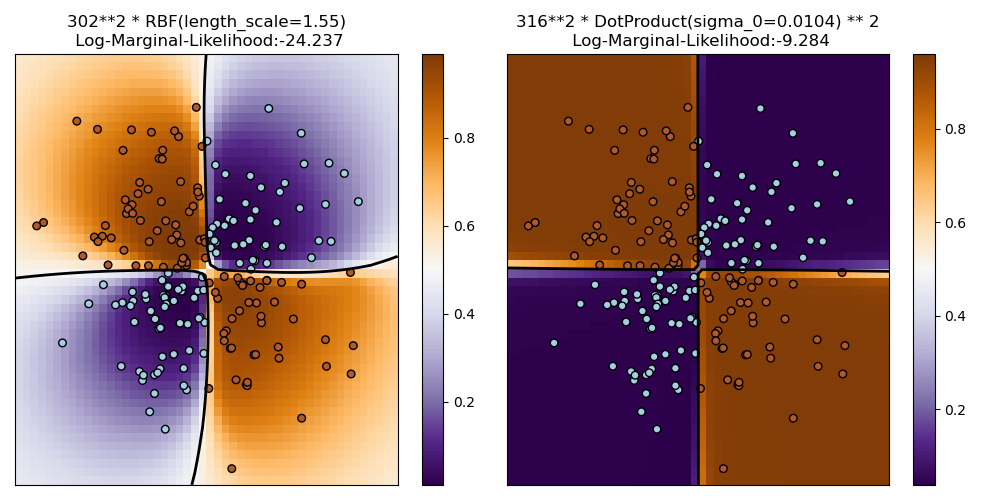
1.7.3.2. Illustration von GPC auf dem XOR-Datensatz#
Dieses Beispiel illustriert GPC auf XOR-Daten. Verglichen werden ein stationärer, isotroper Kernel (RBF) und ein nicht-stationärer Kernel (DotProduct). Auf diesem speziellen Datensatz erzielt der DotProduct-Kernel erheblich bessere Ergebnisse, da die Klassengrenzen linear sind und mit den Koordinatenachsen zusammenfallen. In der Praxis erzielen stationäre Kerne wie RBF jedoch oft bessere Ergebnisse.
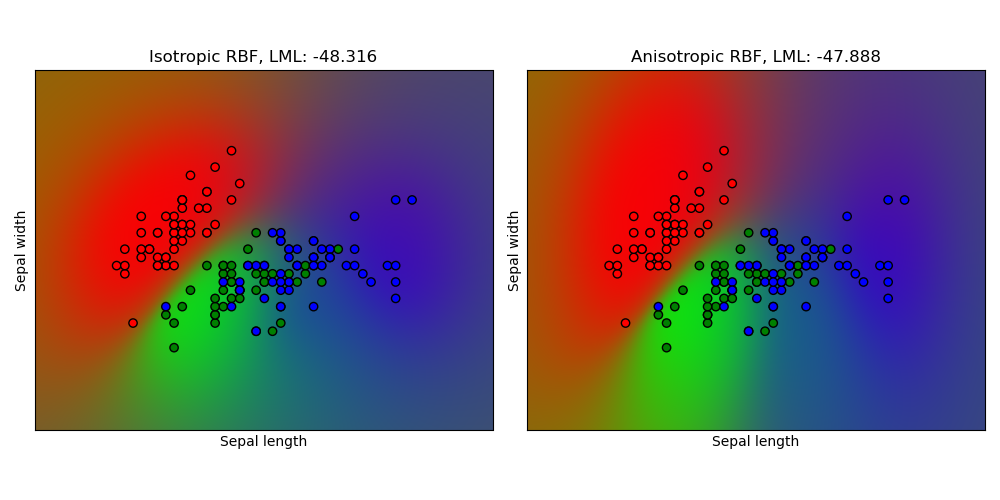
1.7.3.3. Gauß-Prozess-Klassifikation (GPC) auf dem Iris-Datensatz#
Dieses Beispiel illustriert die vorhergesagte Wahrscheinlichkeit von GPC für einen isotropen und anisotropen RBF-Kernel auf einer zweidimensionalen Version des Iris-Datensatzes. Dies illustriert die Anwendbarkeit von GPC auf nicht-binäre Klassifikation. Der anisotrope RBF-Kernel erzielt eine etwas höhere Log-Marginal-Likelihood, indem er unterschiedliche Längenmaßstäbe den beiden Merkmalsdimensionen zuweist.
1.7.4. Kerne für Gauß-Prozesse#
Kerne (im Kontext von GPs auch "Kovarianzfunktionen" genannt) sind eine entscheidende Komponente von GPs, die die Form des Priors und des Posteriors des GPs bestimmen. Sie kodieren die Annahmen über die zu lernende Funktion, indem sie die "Ähnlichkeit" zweier Datenpunkte definieren, kombiniert mit der Annahme, dass ähnliche Datenpunkte ähnliche Zielwerte haben sollten. Zwei Kategorien von Kernen können unterschieden werden: stationäre Kerne hängen nur vom Abstand zweier Datenpunkte ab und nicht von ihren absoluten Werten \(k(x_i, x_j)= k(d(x_i, x_j))\) und sind somit invariant gegenüber Verschiebungen im Eingangsraum, während nicht-stationäre Kerne auch von den spezifischen Werten der Datenpunkte abhängen. Stationäre Kerne können weiter in isotrope und anisotrope Kerne unterteilt werden, wobei isotrope Kerne auch invariant gegenüber Rotationen im Eingangsraum sind. Für weitere Details verweisen wir auf Kapitel 4 von [RW2006]. Dieses Beispiel zeigt, wie ein benutzerdefinierter Kernel über diskrete Daten definiert wird. Anleitungen zur besten Kombination verschiedener Kerne finden Sie in [Duv2014].
Gauß-Prozess-Kernel-API#
Die Hauptanwendung eines Kernel ist die Berechnung der Kovarianz des GP zwischen Datenpunkten. Hierfür kann die Methode __call__ des Kernels aufgerufen werden. Diese Methode kann entweder verwendet werden, um die "Autokovarianz" aller Paare von Datenpunkten in einem 2D-Array X zu berechnen, oder die "Kreuzkovarianz" aller Kombinationen von Datenpunkten eines 2D-Arrays X mit Datenpunkten in einem 2D-Array Y. Die folgende Identität gilt für alle Kerne k (außer für den WhiteKernel): k(X) == K(X, Y=X)
Wenn nur die Diagonale der Autokovarianz verwendet wird, kann die Methode diag() eines Kernels aufgerufen werden, was rechnerisch effizienter ist als der entsprechende Aufruf von __call__: np.diag(k(X, X)) == k.diag(X)
Kerne werden durch einen Vektor \(\theta\) von Hyperparametern parametrisiert. Diese Hyperparameter können zum Beispiel Längenmaßstäbe oder Periodizität eines Kernels steuern (siehe unten). Alle Kerne unterstützen die Berechnung analytischer Gradienten der Autokovarianz des Kernels bezüglich \(log(\theta)\) durch Setzen von eval_gradient=True in der Methode __call__. Das heißt, es wird ein Array der Größe (len(X), len(X), len(theta)) zurückgegeben, wobei der Eintrag [i, j, l] \(\frac{\partial k_\theta(x_i, x_j)}{\partial log(\theta_l)}\) enthält. Dieser Gradient wird vom Gauß-Prozess (sowohl Regressor als auch Klassifikator) bei der Berechnung des Gradienten der Log-Marginal-Likelihood verwendet, der wiederum dazu dient, den Wert von \(\theta\) zu bestimmen, der die Log-Marginal-Likelihood mittels Gradientenaufstieg maximiert. Für jeden Hyperparameter müssen der Anfangswert und die Grenzen bei der Erstellung einer Instanz des Kernels angegeben werden. Der aktuelle Wert von \(\theta\) kann über die Eigenschaft theta des Kernel-Objekts abgefragt und gesetzt werden. Darüber hinaus können die Grenzen der Hyperparameter über die Eigenschaft bounds des Kernels abgerufen werden. Beachten Sie, dass beide Eigenschaften (theta und bounds) log-transformierte Werte der intern verwendeten Werte zurückgeben, da diese typischerweise für gradientenbasierte Optimierung besser geeignet sind. Die Spezifikation jedes Hyperparameters ist in Form einer Instanz von Hyperparameter im jeweiligen Kernel gespeichert. Beachten Sie, dass ein Kernel, der einen Hyperparameter mit dem Namen "x" verwendet, die Attribute self.x und self.x_bounds haben muss.
Die abstrakte Basisklasse für alle Kerne ist Kernel. Kernel implementiert eine ähnliche Schnittstelle wie BaseEstimator und stellt die Methoden get_params(), set_params() und clone() bereit. Dies ermöglicht das Setzen von Kernel-Werten auch über Meta-Estimators wie Pipeline oder GridSearchCV. Beachten Sie, dass aufgrund der verschachtelten Struktur von Kernen (durch Anwendung von Kernel-Operatoren, siehe unten) die Namen von Kernel-Parametern relativ kompliziert werden können. Im Allgemeinen werden für einen binären Kernel-Operator die Parameter des linken Operanden mit k1__ und die Parameter des rechten Operanden mit k2__ präfigiert. Eine zusätzliche Komfortmethode ist clone_with_theta(theta), die eine geklonte Version des Kernels zurückgibt, aber mit den auf theta gesetzten Hyperparametern. Ein anschauliches Beispiel.
>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
k1 : 1**2 * RBF(length_scale=0.5)
k1__k1 : 1**2
k1__k1__constant_value : 1.0
k1__k1__constant_value_bounds : (0.0, 10.0)
k1__k2 : RBF(length_scale=0.5)
k1__k2__length_scale : 0.5
k1__k2__length_scale_bounds : (0.0, 10.0)
k2 : RBF(length_scale=2)
k2__length_scale : 2.0
k2__length_scale_bounds : (0.0, 10.0)
>>> print(kernel.theta) # Note: log-transformed
[ 0. -0.69314718 0.69314718]
>>> print(kernel.bounds) # Note: log-transformed
[[ -inf 2.30258509]
[ -inf 2.30258509]
[ -inf 2.30258509]]
Alle Gauß-Prozess-Kerne sind interoperabel mit sklearn.metrics.pairwise und umgekehrt: Instanzen von Unterklassen von Kernel können als metric an pairwise_kernels aus sklearn.metrics.pairwise übergeben werden. Darüber hinaus können Kernel-Funktionen aus pairwise als GP-Kerne verwendet werden, indem die Wrapper-Klasse PairwiseKernel verwendet wird. Die einzige Einschränkung ist, dass der Gradient der Hyperparameter nicht analytisch, sondern numerisch ist und all diese Kerne nur isotrope Abstände unterstützen. Der Parameter gamma wird als Hyperparameter betrachtet und kann optimiert werden. Die anderen Kernel-Parameter werden direkt bei der Initialisierung gesetzt und bleiben fixiert.
1.7.4.1. Basis-Kerne#
Der ConstantKernel-Kernel kann als Teil eines Product-Kernels verwendet werden, wo er die Magnitude des anderen Faktors (Kernels) skaliert, oder als Teil eines Sum-Kernels, wo er den Mittelwert des Gauß-Prozesses modifiziert. Er hängt von einem Parameter \(constant\_value\) ab. Er ist definiert als
Der Hauptanwendungsfall des WhiteKernel-Kernels ist als Teil eines Summen-Kernels, wo er die Rauschkomponente des Signals erklärt. Das Anpassen seines Parameters \(noise\_level\) entspricht der Schätzung des Rauschlevels. Er ist definiert als
1.7.4.2. Kernel-Operatoren#
Kernel-Operatoren nehmen einen oder zwei Basis-Kerne und kombinieren sie zu einem neuen Kernel. Der Sum-Kernel nimmt zwei Kerne \(k_1\) und \(k_2\) und kombiniert sie über \(k_{sum}(X, Y) = k_1(X, Y) + k_2(X, Y)\). Der Product-Kernel nimmt zwei Kerne \(k_1\) und \(k_2\) und kombiniert sie über \(k_{product}(X, Y) = k_1(X, Y) * k_2(X, Y)\). Der Exponentiation-Kernel nimmt einen Basis-Kernel und einen Skalar-Parameter \(p\) und kombiniert sie über \(k_{exp}(X, Y) = k(X, Y)^p\). Beachten Sie, dass die magischen Methoden __add__, __mul___ und __pow__ auf den Kernel-Objekten überschrieben sind, sodass man z.B. RBF() + RBF() als Abkürzung für Sum(RBF(), RBF()) verwenden kann.
1.7.4.3. Radial-Basis-Funktion (RBF)-Kernel#
Der RBF-Kernel ist ein stationärer Kernel. Er ist auch als "Squared Exponential"-Kernel bekannt. Er wird durch einen Längenmaßstab-Parameter \(l>0\) parametrisiert, der entweder ein Skalar (isotrope Variante des Kernels) oder ein Vektor mit der gleichen Anzahl von Dimensionen wie die Eingaben \(x\) sein kann (anisotrope Variante des Kernels). Der Kernel ist gegeben durch
wobei \(d(\cdot, \cdot)\) der Euklidische Abstand ist. Dieser Kernel ist unendlich oft differenzierbar, was impliziert, dass GPs mit diesem Kernel als Kovarianzfunktion quadratisch gemittelte Ableitungen aller Ordnungen haben und somit sehr glatt sind. Der Prior und der Posterior eines GPs, der aus einem RBF-Kernel resultiert, sind in der folgenden Abbildung dargestellt.
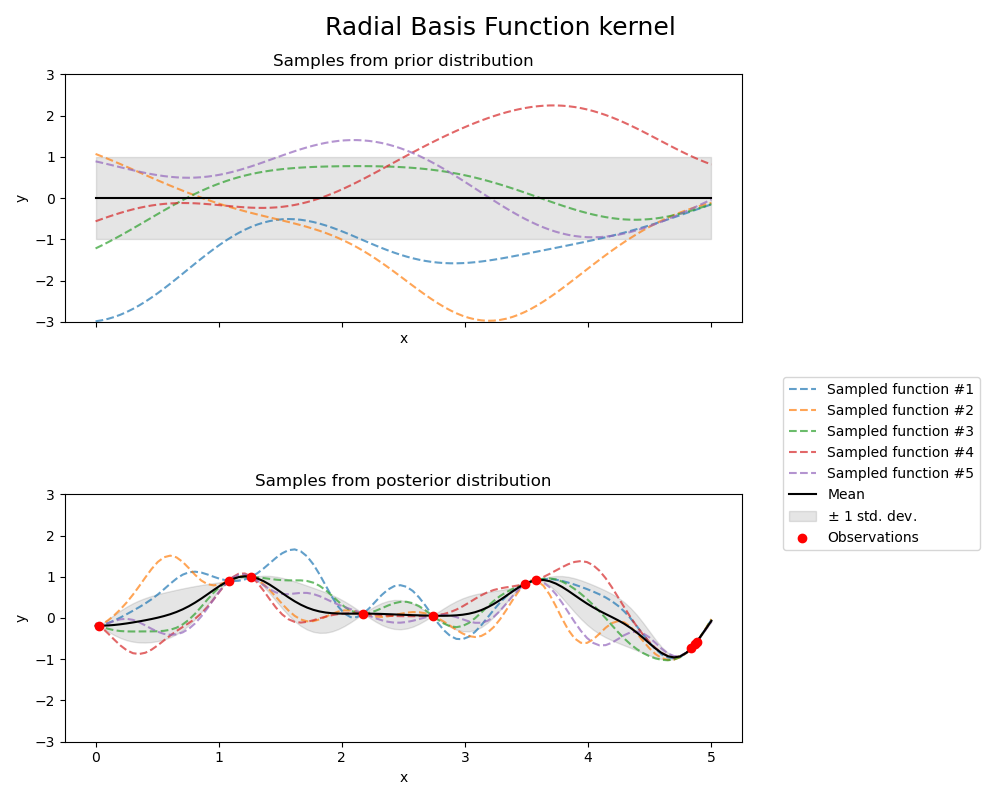
1.7.4.4. Matérn-Kernel#
Der Matern-Kernel ist ein stationärer Kernel und eine Verallgemeinerung des RBF-Kernels. Er hat einen zusätzlichen Parameter \(\nu\), der die Glattheit der resultierenden Funktion steuert. Er wird durch einen Längenmaßstab-Parameter \(l>0\) parametrisiert, der entweder ein Skalar (isotrope Variante des Kernels) oder ein Vektor mit der gleichen Anzahl von Dimensionen wie die Eingaben \(x\) sein kann (anisotrope Variante des Kernels).
Mathematische Implementierung des Matérn-Kernels#
Der Kernel ist gegeben durch
wobei \(d(\cdot,\cdot)\) der Euklidische Abstand, \(K_\nu(\cdot)\) eine modifizierte Besselfunktion und \(\Gamma(\cdot)\) die Gammafunktion ist. Wenn \(\nu\rightarrow\infty\), konvergiert der Matérn-Kernel zum RBF-Kernel. Wenn \(\nu = 1/2\), ist der Matérn-Kernel identisch mit dem absoluten Exponential-Kernel, d.h.
Insbesondere \(\nu = 3/2\)
und \(\nu = 5/2\)
sind beliebte Wahlmöglichkeiten für das Lernen von Funktionen, die nicht unendlich oft differenzierbar sind (wie vom RBF-Kernel angenommen), sondern mindestens einmal (\(\nu = 3/2\)) oder zweimal differenzierbar (\(\nu = 5/2\)).
Die Flexibilität, die Glattheit der gelernten Funktion über \(\nu\) zu steuern, ermöglicht die Anpassung an die Eigenschaften der wahren zugrundeliegenden funktionalen Beziehung.
Der Prior und Posterior eines GPs, der aus einem Matérn-Kernel resultiert, sind in der folgenden Abbildung dargestellt.
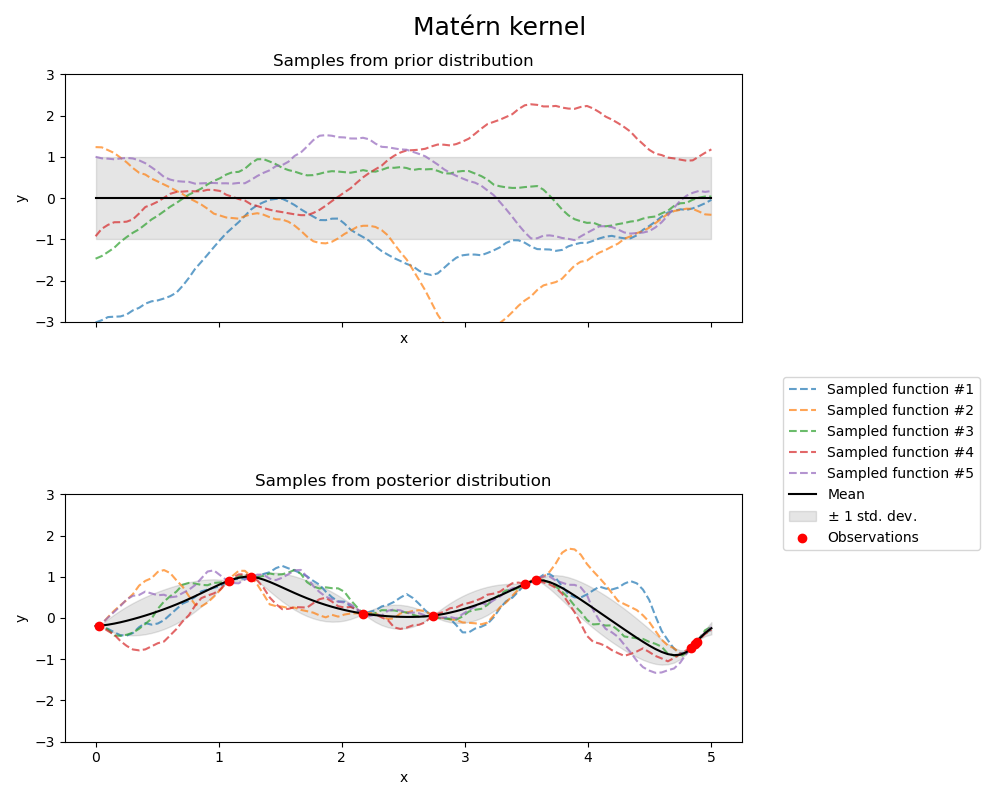
Siehe [RW2006], S. 84 für weitere Details zu den verschiedenen Varianten des Matérn-Kernels.
1.7.4.5. Rational-Quadratic-Kernel#
Der RationalQuadratic-Kernel kann als eine Skalenmischung (eine unendliche Summe) von RBF-Kernels mit unterschiedlichen charakteristischen Längenmaßstäben betrachtet werden. Er wird durch einen Längenmaßstab-Parameter \(l>0\) und einen Skalenmischungs-Parameter \(\alpha>0\) parametrisiert. Derzeit wird nur die isotrope Variante unterstützt, bei der \(l\) ein Skalar ist. Der Kernel ist gegeben durch
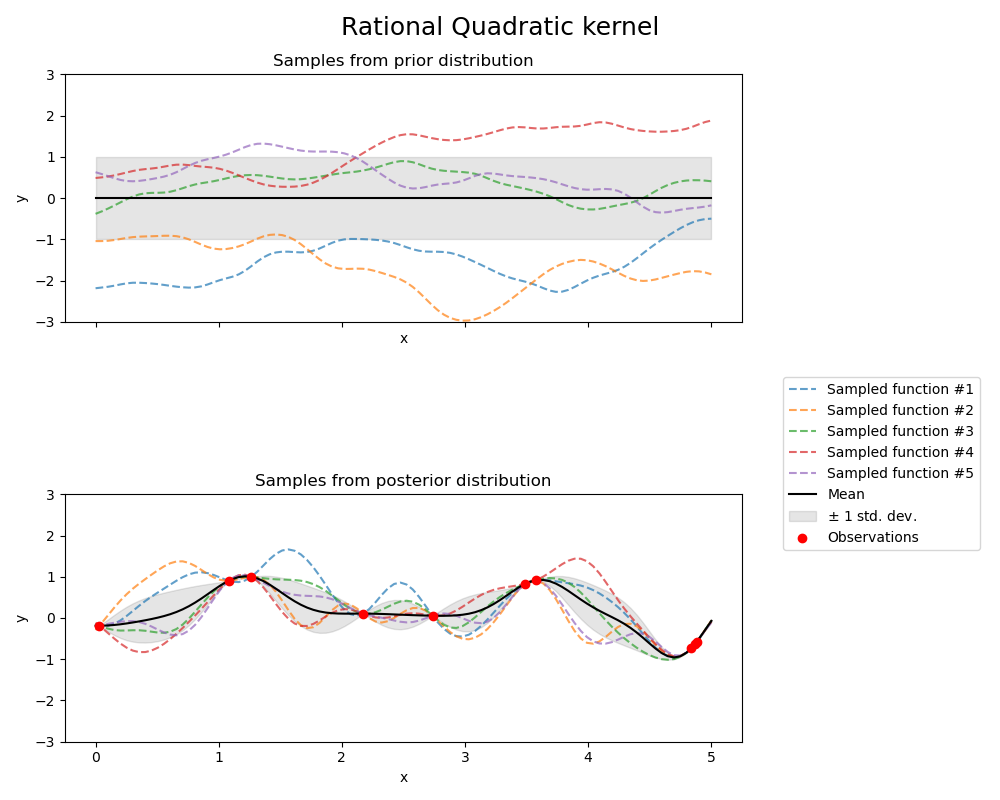
Der Prior und Posterior eines GPs, der aus einem RationalQuadratic-Kernel resultiert, sind in der folgenden Abbildung dargestellt.
1.7.4.6. Exp-Sine-Squared-Kernel#
Der ExpSineSquared-Kernel ermöglicht die Modellierung periodischer Funktionen. Er wird durch einen Längenmaßstab-Parameter \(l>0\) und einen Periodizitäts-Parameter \(p>0\) parametrisiert. Derzeit wird nur die isotrope Variante unterstützt, bei der \(l\) ein Skalar ist. Der Kernel ist gegeben durch
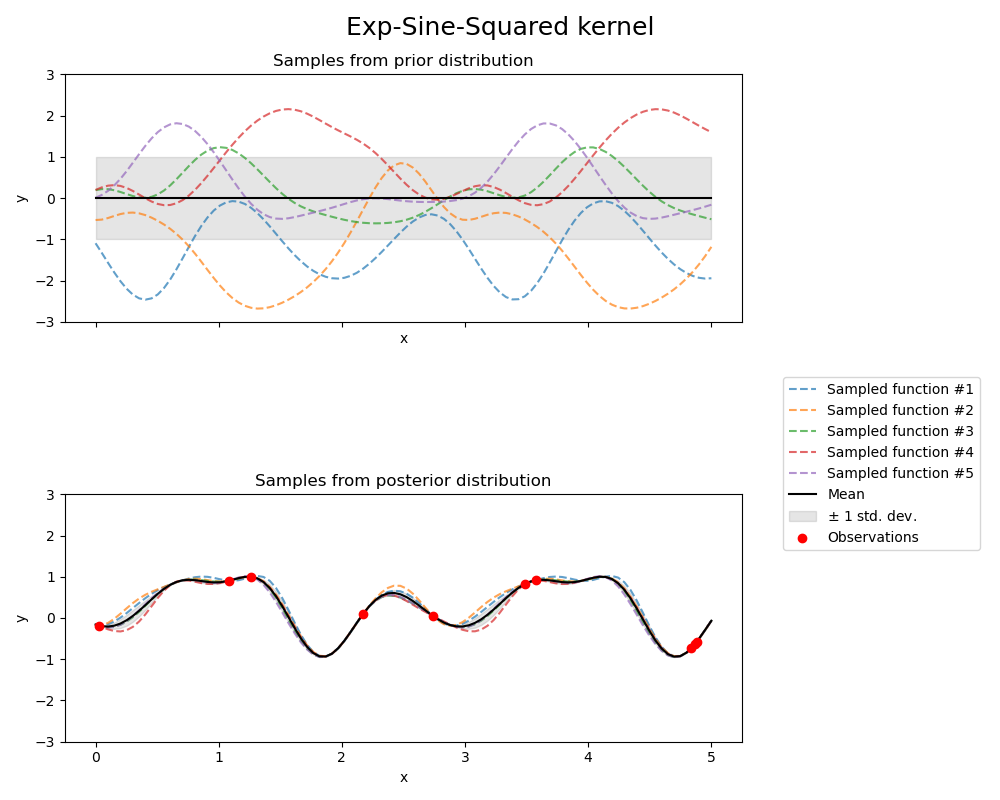
Der Prior und Posterior eines GPs, der aus einem ExpSineSquared-Kernel resultiert, sind in der folgenden Abbildung dargestellt.
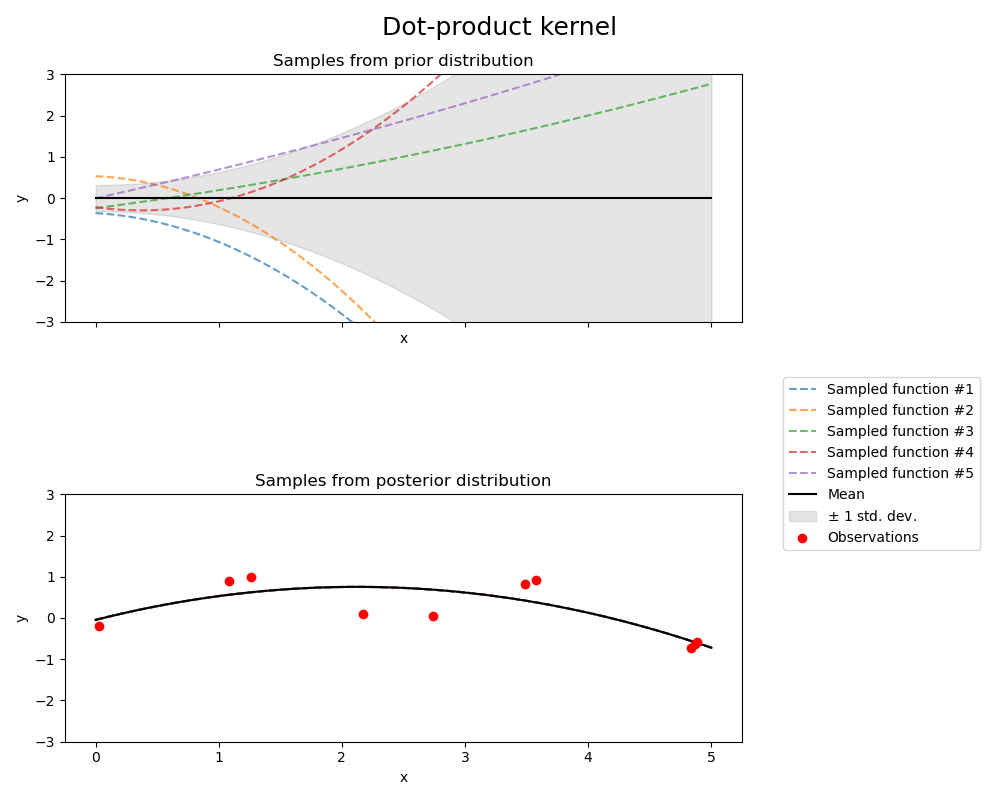
1.7.4.7. Dot-Product-Kernel#
Der DotProduct-Kernel ist nicht-stationär und kann aus der linearen Regression durch das Setzen von \(N(0, 1)\)-Prioris auf die Koeffizienten von \(x_d (d = 1, . . . , D)\) und einer Prior von \(N(0, \sigma_0^2)\) auf den Bias gewonnen werden. Der DotProduct-Kernel ist invariant gegenüber einer Rotation der Koordinaten um den Ursprung, aber nicht gegenüber Translationen. Er wird durch einen Parameter \(\sigma_0^2\) parametrisiert. Für \(\sigma_0^2 = 0\) wird der Kernel als homogener linearer Kernel bezeichnet, andernfalls ist er inhomogen. Der Kernel ist gegeben durch
Der DotProduct-Kernel wird häufig mit Exponentiation kombiniert. Ein Beispiel mit Exponent 2 ist in der folgenden Abbildung dargestellt.