Vergleich von Kernel Ridge und Gauß-Prozess-Regression

Dieses Beispiel veranschaulicht die Unterschiede zwischen einer Kernel Ridge Regression und einer Gauß-Prozess-Regression.

Sowohl die Kernel Ridge Regression als auch die Gauß-Prozess-Regression verwenden einen sogenannten „Kernel-Trick“, um ihre Modelle ausdrucksstark genug zu machen, um die Trainingsdaten anzupassen. Die von den beiden Methoden gelösten maschinellen Lernprobleme sind jedoch drastisch unterschiedlich.

Kernel Ridge Regression findet die Zielfunktion, die eine Verlustfunktion (den mittleren quadratischen Fehler) minimiert.

Anstatt eine einzelne Zielfunktion zu finden, verwendet die Gauß-Prozess-Regression einen probabilistischen Ansatz: Eine Gaußsche A-posteriori-Verteilung über Zielfunktionen wird anhand des Satzes von Bayes definiert. Somit werden A-priori-Wahrscheinlichkeiten für Zielfunktionen mit einer Likelihood-Funktion, die durch die beobachteten Trainingsdaten definiert ist, kombiniert, um Schätzungen der A-posteriori-Verteilungen zu liefern.

Wir werden diese Unterschiede anhand eines Beispiels veranschaulichen und uns auch auf die Feinabstimmung der Kernel-Hyperparameter konzentrieren.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Generieren eines Datensatzes

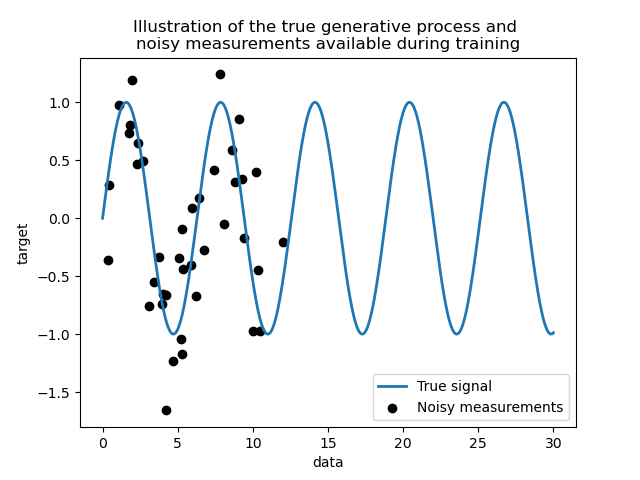
Wir erstellen einen synthetischen Datensatz. Der wahre Generierungsprozess nimmt einen 1D-Vektor und berechnet seinen Sinus. Beachten Sie, dass die Periode dieses Sinus somit \(2 \pi\) beträgt. Wir werden diese Information später in diesem Beispiel wiederverwenden.

import numpy as np

rng = np.random.RandomState(0)
data = np.linspace(0, 30, num=1_000).reshape(-1, 1)
target = np.sin(data).ravel()

Nun können wir uns ein Szenario vorstellen, in dem wir Beobachtungen aus diesem wahren Prozess erhalten. Wir werden jedoch einige Herausforderungen hinzufügen:

• die Messungen werden verrauscht sein;

• nur Stichproben vom Anfang des Signals werden verfügbar sein.

training_sample_indices = rng.choice(np.arange(0, 400), size=40, replace=False)
training_data = data[training_sample_indices]
training_noisy_target = target[training_sample_indices] + 0.5 * rng.randn(
    len(training_sample_indices)
)

Lassen Sie uns das wahre Signal und die verrauschten Messungen, die für das Training verfügbar sind, grafisch darstellen.

import matplotlib.pyplot as plt

plt.plot(data, target, label="True signal", linewidth=2)
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Illustration of the true generative process and \n"
    "noisy measurements available during training"
)

Grenzen eines einfachen linearen Modells

Zunächst möchten wir die Grenzen eines linearen Modells angesichts unseres Datensatzes hervorheben. Wir passen einen Ridge an und überprüfen die Vorhersagen dieses Modells für unseren Datensatz.

from sklearn.linear_model import Ridge

ridge = Ridge().fit(training_data, training_noisy_target)

plt.plot(data, target, label="True signal", linewidth=2)
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(data, ridge.predict(data), label="Ridge regression")
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Limitation of a linear model such as ridge")

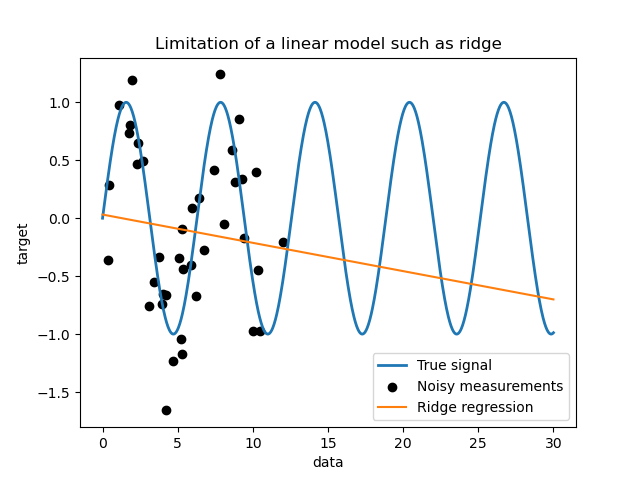
Ein solcher Ridge-Regressor unteranpasst die Daten, da er nicht ausdrucksstark genug ist.

Kernel-Methoden: Kernel Ridge und Gauß-Prozess

Kernel Ridge

Wir können das vorherige lineare Modell ausdrucksstärker machen, indem wir einen sogenannten Kernel verwenden. Ein Kernel ist eine Einbettung vom ursprünglichen Merkmalsraum in einen anderen. Vereinfacht ausgedrückt, wird er verwendet, um unsere Originaldaten in einen neueren und komplexeren Merkmalsraum abzubilden. Dieser neue Raum wird explizit durch die Wahl des Kernels definiert.

In unserem Fall wissen wir, dass der wahre Generierungsprozess eine periodische Funktion ist. Wir können einen ExpSineSquared-Kernel verwenden, der die Periodizität wiederherstellt. Die Klasse KernelRidge akzeptiert einen solchen Kernel.

Die Verwendung dieses Modells zusammen mit einem Kernel ist gleichbedeutend damit, die Daten mithilfe der Abbildungsfunktion des Kernels einzubetten und dann eine Ridge-Regression anzuwenden. In der Praxis werden die Daten nicht explizit abgebildet; stattdessen wird das Skalarprodukt zwischen Stichproben im höherdimensionalen Merkmalsraum mithilfe des „Kernel-Tricks“ berechnet.

Lassen Sie uns also einen solchen KernelRidge verwenden.

import time

from sklearn.gaussian_process.kernels import ExpSineSquared
from sklearn.kernel_ridge import KernelRidge

kernel_ridge = KernelRidge(kernel=ExpSineSquared())

start_time = time.time()
kernel_ridge.fit(training_data, training_noisy_target)
print(
    f"Fitting KernelRidge with default kernel: {time.time() - start_time:.3f} seconds"
)

Fitting KernelRidge with default kernel: 0.001 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(
    data,
    kernel_ridge.predict(data),
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Kernel ridge regression with an exponential sine squared\n "
    "kernel using default hyperparameters"
)

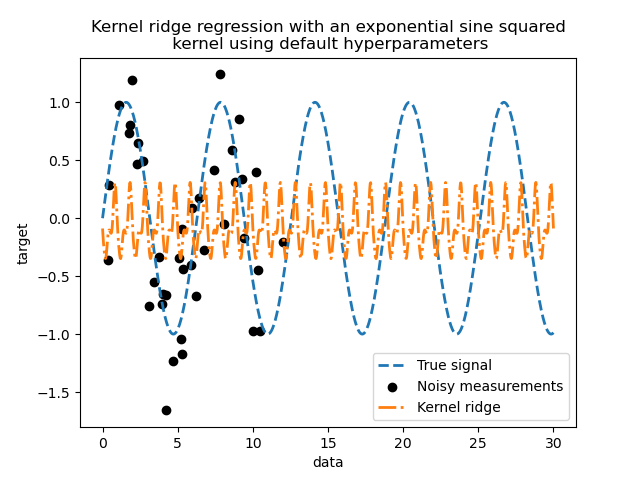
Dieses angepasste Modell ist nicht genau. Tatsächlich haben wir die Parameter des Kernels nicht festgelegt, sondern die Standardwerte verwendet. Wir können sie inspizieren.

kernel_ridge.kernel

ExpSineSquared(length_scale=1, periodicity=1)

Unser Kernel hat zwei Parameter: die Längenskala und die Periodizität. Für unseren Datensatz verwenden wir sin als Generierungsprozess, was eine \(2 \pi\)-Periodizität für das Signal bedeutet. Da der Standardwert des Parameters \(1\) ist, erklärt dies die hohe Frequenz, die in den Vorhersagen unseres Modells beobachtet wird. Ähnliche Schlussfolgerungen könnten für den Längenskala-Parameter gezogen werden. Dies deutet darauf hin, dass die Kernel-Parameter abgestimmt werden müssen. Wir verwenden eine zufällige Suche, um die verschiedenen Parameter des Kernel-Ridge-Modells abzustimmen: den alpha-Parameter und die Kernel-Parameter.

from scipy.stats import loguniform

from sklearn.model_selection import RandomizedSearchCV

param_distributions = {
    "alpha": loguniform(1e0, 1e3),
    "kernel__length_scale": loguniform(1e-2, 1e2),
    "kernel__periodicity": loguniform(1e0, 1e1),
}
kernel_ridge_tuned = RandomizedSearchCV(
    kernel_ridge,
    param_distributions=param_distributions,
    n_iter=500,
    random_state=0,
)
start_time = time.time()
kernel_ridge_tuned.fit(training_data, training_noisy_target)
print(f"Time for KernelRidge fitting: {time.time() - start_time:.3f} seconds")

Time for KernelRidge fitting: 3.604 seconds

Das Anpassen des Modells ist jetzt rechnerisch aufwendiger, da wir mehrere Kombinationen von Hyperparametern ausprobieren müssen. Wir können uns die gefundenen Hyperparameter ansehen, um einige Einblicke zu gewinnen.

kernel_ridge_tuned.best_params_

{'alpha': np.float64(1.991584977345022), 'kernel__length_scale': np.float64(0.7986499491396734), 'kernel__periodicity': np.float64(6.6072758064261095)}

Wenn wir uns die besten Parameter ansehen, stellen wir fest, dass sie sich von den Standardwerten unterscheiden. Wir sehen auch, dass die Periodizität näher am erwarteten Wert liegt: \(2 \pi\). Wir können uns nun die Vorhersagen unseres abgestimmten Kernel Ridge ansehen.

start_time = time.time()
predictions_kr = kernel_ridge_tuned.predict(data)
print(f"Time for KernelRidge predict: {time.time() - start_time:.3f} seconds")

Time for KernelRidge predict: 0.001 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Kernel ridge regression with an exponential sine squared\n "
    "kernel using tuned hyperparameters"
)

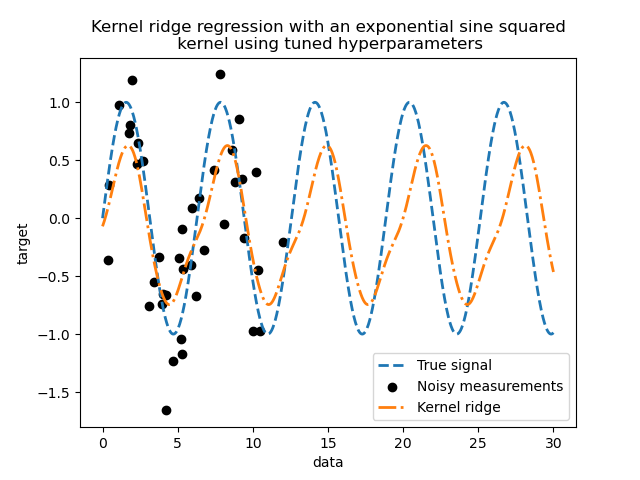
Wir erhalten ein deutlich genaueres Modell. Wir beobachten immer noch einige Fehler, hauptsächlich aufgrund des zum Datensatz hinzugefügten Rauschens.

Gauß-Prozess-Regression

Nun verwenden wir einen GaussianProcessRegressor, um denselben Datensatz anzupassen. Beim Trainieren eines Gauß-Prozesses werden die Hyperparameter des Kernels während des Anpassungsprozesses optimiert. Es ist keine externe Hyperparameter-Suche erforderlich. Hier erstellen wir einen etwas komplexeren Kernel als für den Kernel-Ridge-Regressor: Wir fügen einen WhiteKernel hinzu, der zur Schätzung des Rauschens im Datensatz verwendet wird.

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel

kernel = 1.0 * ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) + WhiteKernel(
    1e-1
)
gaussian_process = GaussianProcessRegressor(kernel=kernel)
start_time = time.time()
gaussian_process.fit(training_data, training_noisy_target)
print(
    f"Time for GaussianProcessRegressor fitting: {time.time() - start_time:.3f} seconds"
)

Time for GaussianProcessRegressor fitting: 0.028 seconds

Der Rechenaufwand für das Trainieren eines Gauß-Prozesses ist deutlich geringer als bei der Kernel Ridge, die eine zufällige Suche verwendet. Wir können die Parameter der berechneten Kernel überprüfen.

gaussian_process.kernel_

0.675**2 * ExpSineSquared(length_scale=1.34, periodicity=6.57) + WhiteKernel(noise_level=0.182)

Tatsächlich sehen wir, dass die Parameter optimiert wurden. Wenn wir uns den Parameter periodicity ansehen, stellen wir fest, dass wir eine Periode nahe dem theoretischen Wert \(2 \pi\) gefunden haben. Wir können uns nun die Vorhersagen unseres Modells ansehen.

start_time = time.time()
mean_predictions_gpr, std_predictions_gpr = gaussian_process.predict(
    data,
    return_std=True,
)
print(
    f"Time for GaussianProcessRegressor predict: {time.time() - start_time:.3f} seconds"
)

Time for GaussianProcessRegressor predict: 0.002 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
# Plot the predictions of the kernel ridge
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
# Plot the predictions of the gaussian process regressor
plt.plot(
    data,
    mean_predictions_gpr,
    label="Gaussian process regressor",
    linewidth=2,
    linestyle="dotted",
)
plt.fill_between(
    data.ravel(),
    mean_predictions_gpr - std_predictions_gpr,
    mean_predictions_gpr + std_predictions_gpr,
    color="tab:green",
    alpha=0.2,
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Comparison between kernel ridge and gaussian process regressor")

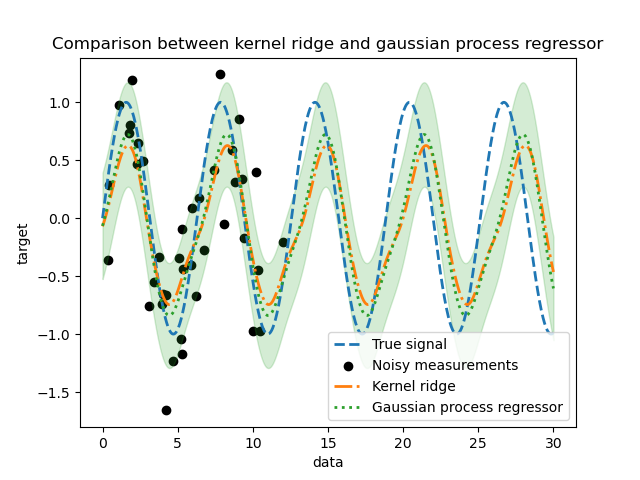
Wir beobachten, dass die Ergebnisse des Kernel Ridge und des Gauß-Prozess-Regressors nahe beieinander liegen. Der Gauß-Prozess-Regressor liefert jedoch auch eine Unsicherheitsinformation, die bei einem Kernel Ridge nicht verfügbar ist. Aufgrund der probabilistischen Formulierung der Zielfunktionen kann der Gauß-Prozess die Standardabweichung (oder die Kovarianz) zusammen mit den Mittelwertvorhersagen der Zielfunktionen ausgeben.

Dies hat jedoch seinen Preis: Die Rechenzeit für die Vorhersagen ist bei einem Gauß-Prozess höher.

Abschließende Schlussfolgerung

Wir können noch etwas zur Extrapolationsfähigkeit der beiden Modelle sagen. Tatsächlich haben wir nur den Anfang des Signals als Trainingsset bereitgestellt. Die Verwendung eines periodischen Kernels zwingt unser Modell, das auf dem Trainingsset gefundene Muster zu wiederholen. Unter Verwendung dieser Kernel-Informationen zusammen mit der Fähigkeit beider Modelle zur Extrapolation beobachten wir, dass die Modelle weiterhin das Sinusmuster vorhersagen werden.

Gauß-Prozess ermöglicht die Kombination von Kernels. So könnten wir den exponentiellen Sinus-Quadrat-Kernel mit einem Radial-Basis-Funktions-Kernel kombinieren.

from sklearn.gaussian_process.kernels import RBF

kernel = 1.0 * ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) * RBF(
    length_scale=15, length_scale_bounds="fixed"
) + WhiteKernel(1e-1)
gaussian_process = GaussianProcessRegressor(kernel=kernel)
gaussian_process.fit(training_data, training_noisy_target)
mean_predictions_gpr, std_predictions_gpr = gaussian_process.predict(
    data,
    return_std=True,
)

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
# Plot the predictions of the kernel ridge
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
# Plot the predictions of the gaussian process regressor
plt.plot(
    data,
    mean_predictions_gpr,
    label="Gaussian process regressor",
    linewidth=2,
    linestyle="dotted",
)
plt.fill_between(
    data.ravel(),
    mean_predictions_gpr - std_predictions_gpr,
    mean_predictions_gpr + std_predictions_gpr,
    color="tab:green",
    alpha=0.2,
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Effect of using a radial basis function kernel")

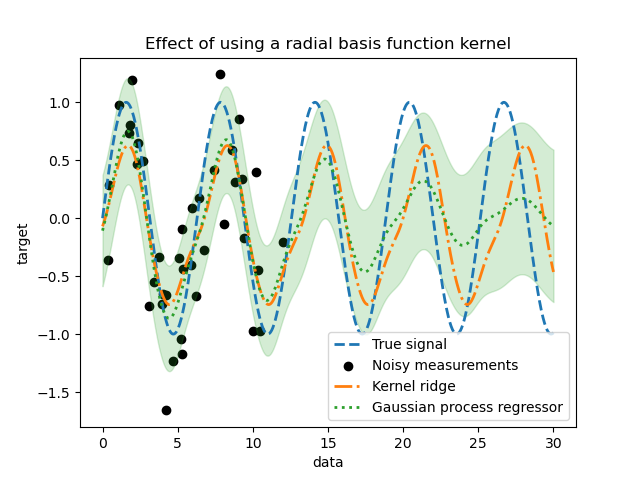
Der Effekt der Verwendung eines Radial-Basis-Funktions-Kernels wird den Periodizitätseffekt abschwächen, sobald keine Stichproben im Training verfügbar sind. Wenn die Teststichproben weiter von den Trainingsstichproben entfernt sind, konvergieren die Vorhersagen zu ihrem Mittelwert, und ihre Standardabweichung nimmt ebenfalls zu.

Verwandte Beispiele

Gauß-Prozesse Regression: grundlegendes Einführungsexempel

Gauß-Prozesse Regression: grundlegendes Einführungsexempel

HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern

HuberRegressor vs Ridge auf Datensatz mit starken Ausreißern

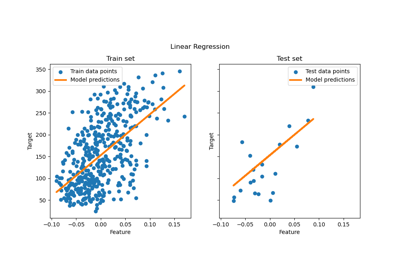
Gewöhnliche kleinste Quadrate und Ridge Regression

Gewöhnliche kleinste Quadrate und Ridge Regression

Ridge-Koeffizienten als Funktion der Regularisierung plotten

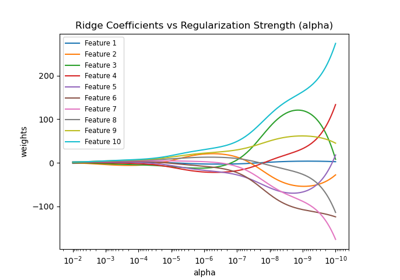
Ridge-Koeffizienten als Funktion der Regularisierung plotten