IsolationForest Beispiel

Ein Beispiel für die Verwendung von IsolationForest zur Anomalieerkennung.

Der Isolation Forest ist ein Ensemble von „Isolation Trees“, die Beobachtungen durch rekursives zufälliges Partitionieren „isolieren“, was durch eine Baumstruktur dargestellt werden kann. Die Anzahl der Aufteilungen, die zur Isolierung einer Stichprobe erforderlich sind, ist für Ausreißer geringer und für Inlierer höher.

Im vorliegenden Beispiel demonstrieren wir zwei Möglichkeiten, die Entscheidungsgrenze eines auf einem Spiel-Datensatz trainierten Isolation Forest zu visualisieren.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datengenerierung

Wir generieren zwei Cluster (jeder enthält n_samples), indem wir die Standardnormalverteilung zufällig auswählen, wie sie von numpy.random.randn zurückgegeben wird. Einer davon ist kugelförmig und der andere ist leicht verformt.

Zur Konsistenz mit der IsolationForest-Notation werden die Inlierer (d. h. die Gauß-Cluster) mit dem Ground-Truth-Label 1 und die Ausreißer (erstellt mit numpy.random.uniform) mit dem Label -1 gekennzeichnet.

import numpy as np

from sklearn.model_selection import train_test_split

n_samples, n_outliers = 120, 40
rng = np.random.RandomState(0)
covariance = np.array([[0.5, -0.1], [0.7, 0.4]])
cluster_1 = 0.4 * rng.randn(n_samples, 2) @ covariance + np.array([2, 2])  # general
cluster_2 = 0.3 * rng.randn(n_samples, 2) + np.array([-2, -2])  # spherical
outliers = rng.uniform(low=-4, high=4, size=(n_outliers, 2))

X = np.concatenate([cluster_1, cluster_2, outliers])
y = np.concatenate(
    [np.ones((2 * n_samples), dtype=int), -np.ones((n_outliers), dtype=int)]
)

X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

Wir können die resultierenden Cluster visualisieren

import matplotlib.pyplot as plt

scatter = plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor="k")
handles, labels = scatter.legend_elements()
plt.axis("square")
plt.legend(handles=handles, labels=["outliers", "inliers"], title="true class")
plt.title("Gaussian inliers with \nuniformly distributed outliers")
plt.show()

Training des Modells

from sklearn.ensemble import IsolationForest

clf = IsolationForest(max_samples=100, random_state=0)
clf.fit(X_train)

IsolationForest(max_samples=100, random_state=0)

In einer Jupyter-Umgebung führen Sie diese Zelle bitte erneut aus, um die HTML-Darstellung anzuzeigen, oder vertrauen Sie dem Notebook.
Auf GitHub kann die HTML-Darstellung nicht gerendert werden. Versuchen Sie bitte, diese Seite mit nbviewer.org zu laden.

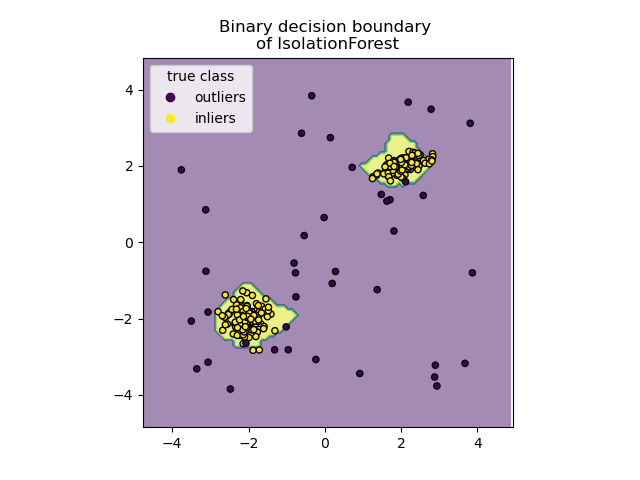
Diskrete Entscheidungsgrenze plotten

Wir verwenden die Klasse DecisionBoundaryDisplay, um eine diskrete Entscheidungsgrenze zu visualisieren. Die Hintergrundfarbe repräsentiert, ob eine Stichprobe in dem gegebenen Bereich als Ausreißer vorhergesagt wird oder nicht. Das Streudiagramm zeigt die wahren Labels.

import matplotlib.pyplot as plt

from sklearn.inspection import DecisionBoundaryDisplay

disp = DecisionBoundaryDisplay.from_estimator(
    clf,
    X,
    response_method="predict",
    alpha=0.5,
)
disp.ax_.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor="k")
disp.ax_.set_title("Binary decision boundary \nof IsolationForest")
plt.axis("square")
plt.legend(handles=handles, labels=["outliers", "inliers"], title="true class")
plt.show()

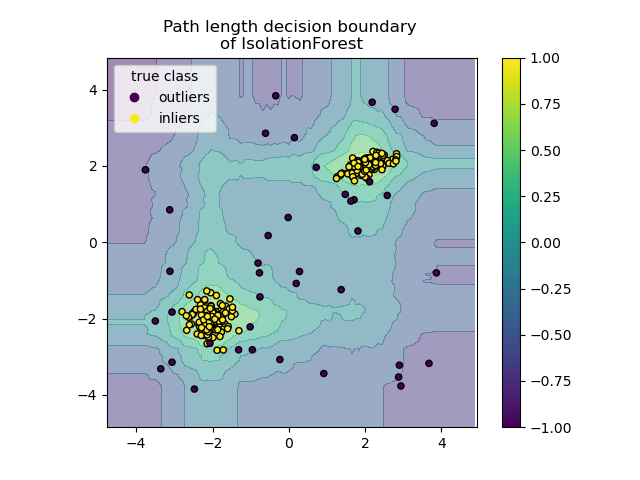
Pfadlängen-Entscheidungsgrenze plotten

Durch Setzen von response_method="decision_function" repräsentiert der Hintergrund des DecisionBoundaryDisplay das Maß für die Normalität einer Beobachtung. Ein solcher Score ergibt sich aus der Pfadlänge, die über einen Wald von Zufallsbäumen gemittelt wird, was wiederum durch die Tiefe des Blattes (oder gleichwertig die Anzahl der Teilungen) gegeben ist, die zur Isolierung einer gegebenen Stichprobe erforderlich sind.

Wenn ein Wald von Zufallsbäumen gemeinsam kurze Pfadlängen zur Isolierung bestimmter Stichproben erzeugt, sind diese höchstwahrscheinlich Anomalien und das Maß für die Normalität liegt nahe bei 0. Ähnlich entsprechen große Pfade Werten nahe bei 1 und sind eher Inlierer.

disp = DecisionBoundaryDisplay.from_estimator(
    clf,
    X,
    response_method="decision_function",
    alpha=0.5,
)
disp.ax_.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor="k")
disp.ax_.set_title("Path length decision boundary \nof IsolationForest")
plt.axis("square")
plt.legend(handles=handles, labels=["outliers", "inliers"], title="true class")
plt.colorbar(disp.ax_.collections[1])
plt.show()

Verwandte Beispiele

Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Toy-Datensätzen

Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Toy-Datensätzen

Zwei-Klassen-AdaBoost

Zwei-Klassen-AdaBoost

Nearest Neighbors Klassifikation

Nearest Neighbors Klassifikation

Theil-Sen Regression

Theil-Sen Regression