Permutation Importance bei multikollinearen oder korrelierten Merkmalen

In diesem Beispiel berechnen wir die permutation_importance der Merkmale für einen trainierten RandomForestClassifier unter Verwendung des Brustkrebs Wisconsin (Diagnostik) Datensatzes. Das Modell kann auf einem Testdatensatz leicht eine Genauigkeit von etwa 97 % erzielen. Da dieser Datensatz multikollineare Merkmale enthält, zeigt die Permutationswichtigkeit, dass keines der Merkmale wichtig ist, was im Widerspruch zur hohen Testgenauigkeit steht.

Wir demonstrieren einen möglichen Ansatz zur Handhabung von Multikollinearität, der darin besteht, ein hierarchisches Clustering auf den Spearman-Rangkorrelationskoeffizienten der Merkmale durchzuführen, einen Schwellenwert zu wählen und ein einzelnes Merkmal aus jedem Cluster zu behalten.

Hinweis

Siehe auch Permutation Importance vs Random Forest Feature Importance (MDI)

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Random Forest Feature Importance auf Brustkrebsdaten

Zuerst definieren wir eine Funktion zur Erleichterung der Darstellung.

import matplotlib

from sklearn.inspection import permutation_importance
from sklearn.utils.fixes import parse_version


def plot_permutation_importance(clf, X, y, ax):
    result = permutation_importance(clf, X, y, n_repeats=10, random_state=42, n_jobs=2)
    perm_sorted_idx = result.importances_mean.argsort()

    # `labels` argument in boxplot is deprecated in matplotlib 3.9 and has been
    # renamed to `tick_labels`. The following code handles this, but as a
    # scikit-learn user you probably can write simpler code by using `labels=...`
    # (matplotlib < 3.9) or `tick_labels=...` (matplotlib >= 3.9).
    tick_labels_parameter_name = (
        "tick_labels"
        if parse_version(matplotlib.__version__) >= parse_version("3.9")
        else "labels"
    )
    tick_labels_dict = {tick_labels_parameter_name: X.columns[perm_sorted_idx]}
    ax.boxplot(result.importances[perm_sorted_idx].T, vert=False, **tick_labels_dict)
    ax.axvline(x=0, color="k", linestyle="--")
    return ax

Anschließend trainieren wir einen RandomForestClassifier auf dem Brustkrebs Wisconsin (Diagnostik) Datensatz und evaluieren seine Genauigkeit auf einem Testdatensatz.

from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split

X, y = load_breast_cancer(return_X_y=True, as_frame=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

clf = RandomForestClassifier(n_estimators=100, random_state=42)
clf.fit(X_train, y_train)
print(f"Baseline accuracy on test data: {clf.score(X_test, y_test):.2}")

Baseline accuracy on test data: 0.97

Als Nächstes plotten wir die baumbasierte Merkmalwichtigkeit und die Permutationswichtigkeit. Die Permutationswichtigkeit wird auf dem Trainingsdatensatz berechnet, um zu zeigen, wie stark das Modell bei jedem Merkmal während des Trainings angewiesen ist.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

mdi_importances = pd.Series(clf.feature_importances_, index=X_train.columns)
tree_importance_sorted_idx = np.argsort(clf.feature_importances_)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 8))
mdi_importances.sort_values().plot.barh(ax=ax1)
ax1.set_xlabel("Gini importance")
plot_permutation_importance(clf, X_train, y_train, ax2)
ax2.set_xlabel("Decrease in accuracy score")
fig.suptitle(
    "Impurity-based vs. permutation importances on multicollinear features (train set)"
)
_ = fig.tight_layout()

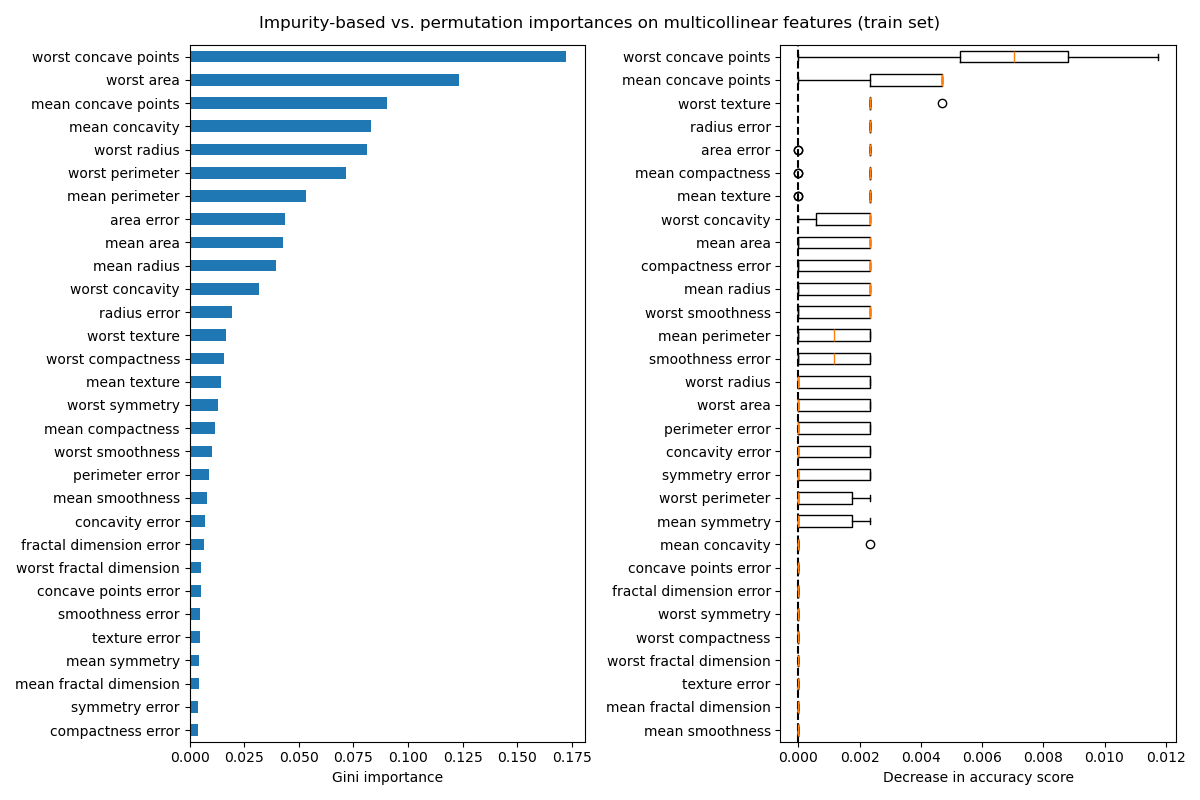
Das Diagramm auf der linken Seite zeigt die Gini-Wichtigkeit des Modells. Da die scikit-learn-Implementierung von RandomForestClassifier bei jedem Split eine zufällige Teilmenge von \(\sqrt{n_\text{features}}\) Merkmalen verwendet, kann sie die Dominanz eines einzelnen korrelierten Merkmals verwässern. Infolgedessen kann die individuelle Merkmalwichtigkeit gleichmäßiger auf die korrelierten Merkmale verteilt werden. Da die Merkmale eine hohe Kardinalität aufweisen und der Klassifikator nicht überangepasst ist, können wir diesen Werten relativ vertrauen.

Die Permutationswichtigkeit im rechten Diagramm zeigt, dass das Permutieren eines Merkmals die Genauigkeit um höchstens 0.012 reduziert, was darauf hindeuten würde, dass keines der Merkmale wichtig ist. Dies steht im Widerspruch zur hohen Testgenauigkeit, die als Basislinie berechnet wurde: Einige Merkmale müssen wichtig sein.

In ähnlicher Weise scheint die Änderung des auf dem Testdatensatz berechneten Genauigkeitswerts zufällig bedingt zu sein.

fig, ax = plt.subplots(figsize=(7, 6))
plot_permutation_importance(clf, X_test, y_test, ax)
ax.set_title("Permutation Importances on multicollinear features\n(test set)")
ax.set_xlabel("Decrease in accuracy score")
_ = ax.figure.tight_layout()

Nichtsdestotrotz kann in Gegenwart korrelierter Merkmale immer noch eine aussagekräftige Permutationswichtigkeit berechnet werden, wie im folgenden Abschnitt gezeigt.

Handhabung multikollinearer Merkmale

Wenn Merkmale kollinear sind, hat das Permutieren eines Merkmals wenig Auswirkung auf die Leistung des Modells, da es dieselben Informationen von einem korrelierten Merkmal erhalten kann. Beachten Sie, dass dies nicht für alle prädiktiven Modelle der Fall ist und von deren zugrunde liegender Implementierung abhängt.

Eine Möglichkeit, multikollineare Merkmale zu handhaben, besteht darin, ein hierarchisches Clustering auf den Spearman-Rangkorrelationskoeffizienten durchzuführen, einen Schwellenwert zu wählen und ein einzelnes Merkmal aus jedem Cluster zu behalten. Zuerst plotten wir eine Heatmap der korrelierten Merkmale.

from scipy.cluster import hierarchy
from scipy.spatial.distance import squareform
from scipy.stats import spearmanr

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 8))
corr = spearmanr(X).correlation

# Ensure the correlation matrix is symmetric
corr = (corr + corr.T) / 2
np.fill_diagonal(corr, 1)

# We convert the correlation matrix to a distance matrix before performing
# hierarchical clustering using Ward's linkage.
distance_matrix = 1 - np.abs(corr)
dist_linkage = hierarchy.ward(squareform(distance_matrix))
dendro = hierarchy.dendrogram(
    dist_linkage, labels=X.columns.to_list(), ax=ax1, leaf_rotation=90
)
dendro_idx = np.arange(0, len(dendro["ivl"]))

ax2.imshow(corr[dendro["leaves"], :][:, dendro["leaves"]])
ax2.set_xticks(dendro_idx)
ax2.set_yticks(dendro_idx)
ax2.set_xticklabels(dendro["ivl"], rotation="vertical")
ax2.set_yticklabels(dendro["ivl"])
_ = fig.tight_layout()

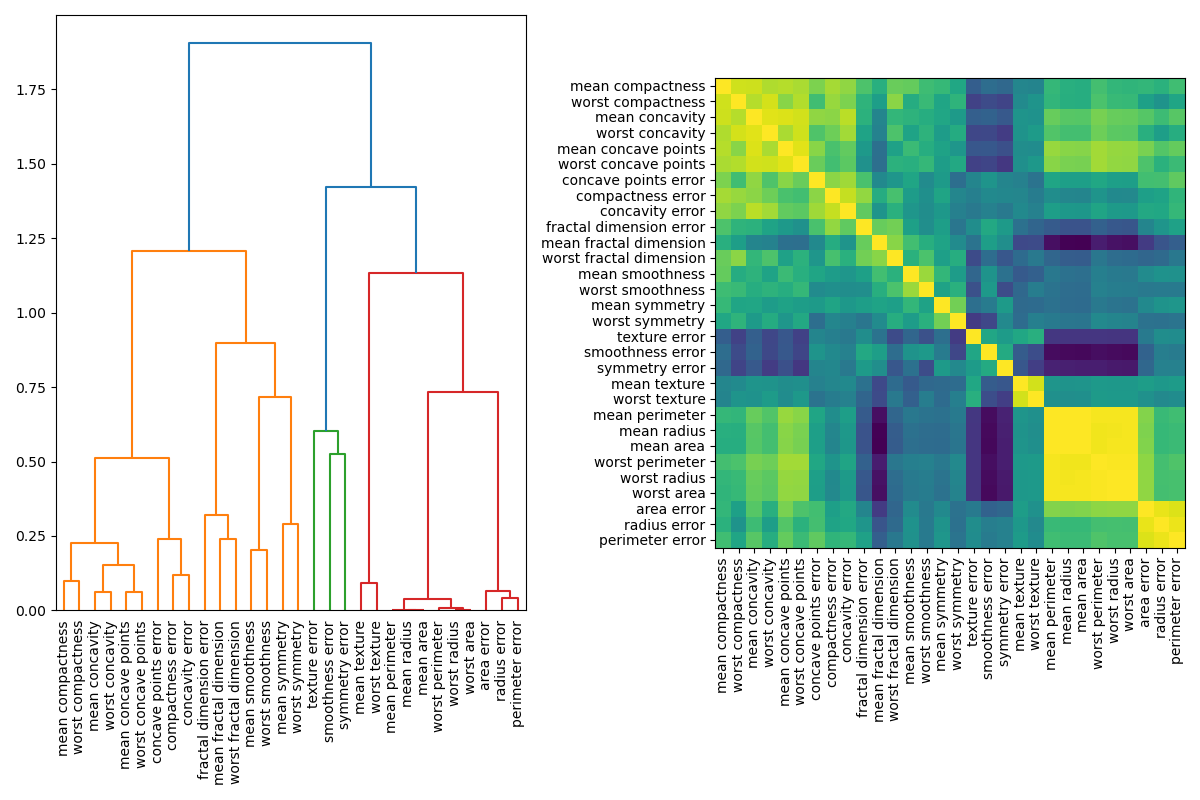
Als Nächstes wählen wir manuell einen Schwellenwert durch visuelle Inspektion des Dendrogramms, um unsere Merkmale in Cluster zu gruppieren und ein Merkmal aus jedem Cluster auszuwählen, das wir behalten möchten, wählen diese Merkmale aus unserem Datensatz aus und trainieren einen neuen Random Forest. Die Testgenauigkeit des neuen Random Forest hat sich im Vergleich zum auf dem vollständigen Datensatz trainierten Random Forest nicht wesentlich verändert.

from collections import defaultdict

cluster_ids = hierarchy.fcluster(dist_linkage, 1, criterion="distance")
cluster_id_to_feature_ids = defaultdict(list)
for idx, cluster_id in enumerate(cluster_ids):
    cluster_id_to_feature_ids[cluster_id].append(idx)
selected_features = [v[0] for v in cluster_id_to_feature_ids.values()]
selected_features_names = X.columns[selected_features]

X_train_sel = X_train[selected_features_names]
X_test_sel = X_test[selected_features_names]

clf_sel = RandomForestClassifier(n_estimators=100, random_state=42)
clf_sel.fit(X_train_sel, y_train)
print(
    "Baseline accuracy on test data with features removed:"
    f" {clf_sel.score(X_test_sel, y_test):.2}"
)

Baseline accuracy on test data with features removed: 0.97

Schließlich können wir die Permutationswichtigkeit des ausgewählten Teilmengen von Merkmalen untersuchen.

fig, ax = plt.subplots(figsize=(7, 6))
plot_permutation_importance(clf_sel, X_test_sel, y_test, ax)
ax.set_title("Permutation Importances on selected subset of features\n(test set)")
ax.set_xlabel("Decrease in accuracy score")
ax.figure.tight_layout()
plt.show()

Verwandte Beispiele

Permutations-Wichtigkeit vs. Random Forest Merkmals-Wichtigkeit (MDI)

Permutations-Wichtigkeit vs. Random Forest Merkmals-Wichtigkeit (MDI)

Merkmalswichtigkeiten mit einem Wald von Bäumen

Merkmalswichtigkeiten mit einem Wald von Bäumen

Gradient Boosting Regression

Gradient Boosting Regression

Release Highlights für scikit-learn 0.22

Release Highlights für scikit-learn 0.22