Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Features in Histogram Gradient Boosting Trees#
Histogrammbasierte Gradient Boosting (HGBT) Modelle sind möglicherweise eine der nützlichsten Modelle für überwachtes Lernen in scikit-learn. Sie basieren auf einer modernen Gradient Boosting-Implementierung, vergleichbar mit LightGBM und XGBoost. Daher sind HGBT-Modelle funktionsreicher und übertreffen oft alternative Modelle wie Random Forests, insbesondere wenn die Anzahl der Samples größer als einige zehntausend ist (siehe Vergleich von Random Forests und Histogramm Gradient Boosting Modellen).
Die wichtigsten Benutzerfreundlichkeitsmerkmale von HGBT-Modellen sind
Mehrere verfügbare Verlustfunktionen für Mittelwert- und Quantilregressionsaufgaben, siehe Quantilverlust.
Unterstützung für kategoriale Merkmale, siehe Unterstützung kategorialer Merkmale in Gradient Boosting.
Frühes Stoppen.
Unterstützung für fehlende Werte, was die Notwendigkeit eines Imputers vermeidet.
Dieses Beispiel zielt darauf ab, alle Punkte außer 2 und 6 in einer realen Umgebung zu demonstrieren.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Vorbereitung der Daten#
Der Stromdatensatz besteht aus Daten, die aus dem australischen New South Wales Electricity Market gesammelt wurden. In diesem Markt sind die Preise nicht fest und werden von Angebot und Nachfrage beeinflusst. Sie werden alle fünf Minuten festgelegt. Stromübertragungen von/nach dem benachbarten Bundesstaat Victoria wurden durchgeführt, um Schwankungen zu lindern.
Der Datensatz, ursprünglich ELEC2 genannt, enthält 45.312 Instanzen vom 7. Mai 1996 bis zum 5. Dezember 1998. Jede Stichprobe des Datensatzes bezieht sich auf einen Zeitraum von 30 Minuten, d.h. es gibt 48 Instanzen für jeden Zeitraum eines Tages. Jede Stichprobe im Datensatz hat 7 Spalten
date: zwischen 7. Mai 1996 und 5. Dezember 1998. Normalisiert zwischen 0 und 1;
day: Wochentag (1-7);
period: halbstündliche Intervalle über 24 Stunden. Normalisiert zwischen 0 und 1;
nswprice/nswdemand: Strompreis/Nachfrage von New South Wales;
vicprice/vicdemand: Strompreis/Nachfrage von Victoria.
Ursprünglich ist es eine Klassifizierungsaufgabe, aber hier verwenden wir es für die Regressionsaufgabe, um die geplante Stromübertragung zwischen den Staaten vorherzusagen.
from sklearn.datasets import fetch_openml
electricity = fetch_openml(
name="electricity", version=1, as_frame=True, parser="pandas"
)
df = electricity.frame
Dieser spezielle Datensatz hat ein stufenweises konstantes Ziel für die ersten 17.760 Stichproben
df["transfer"][:17_760].unique()
array([0.414912, 0.500526])
Lassen Sie uns diese Einträge verwerfen und die stündliche Stromübertragung an verschiedenen Wochentagen untersuchen
import matplotlib.pyplot as plt
import seaborn as sns
df = electricity.frame.iloc[17_760:]
X = df.drop(columns=["transfer", "class"])
y = df["transfer"]
fig, ax = plt.subplots(figsize=(15, 10))
pointplot = sns.lineplot(x=df["period"], y=df["transfer"], hue=df["day"], ax=ax)
handles, labels = ax.get_legend_handles_labels()
ax.set(
title="Hourly energy transfer for different days of the week",
xlabel="Normalized time of the day",
ylabel="Normalized energy transfer",
)
_ = ax.legend(handles, ["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"])
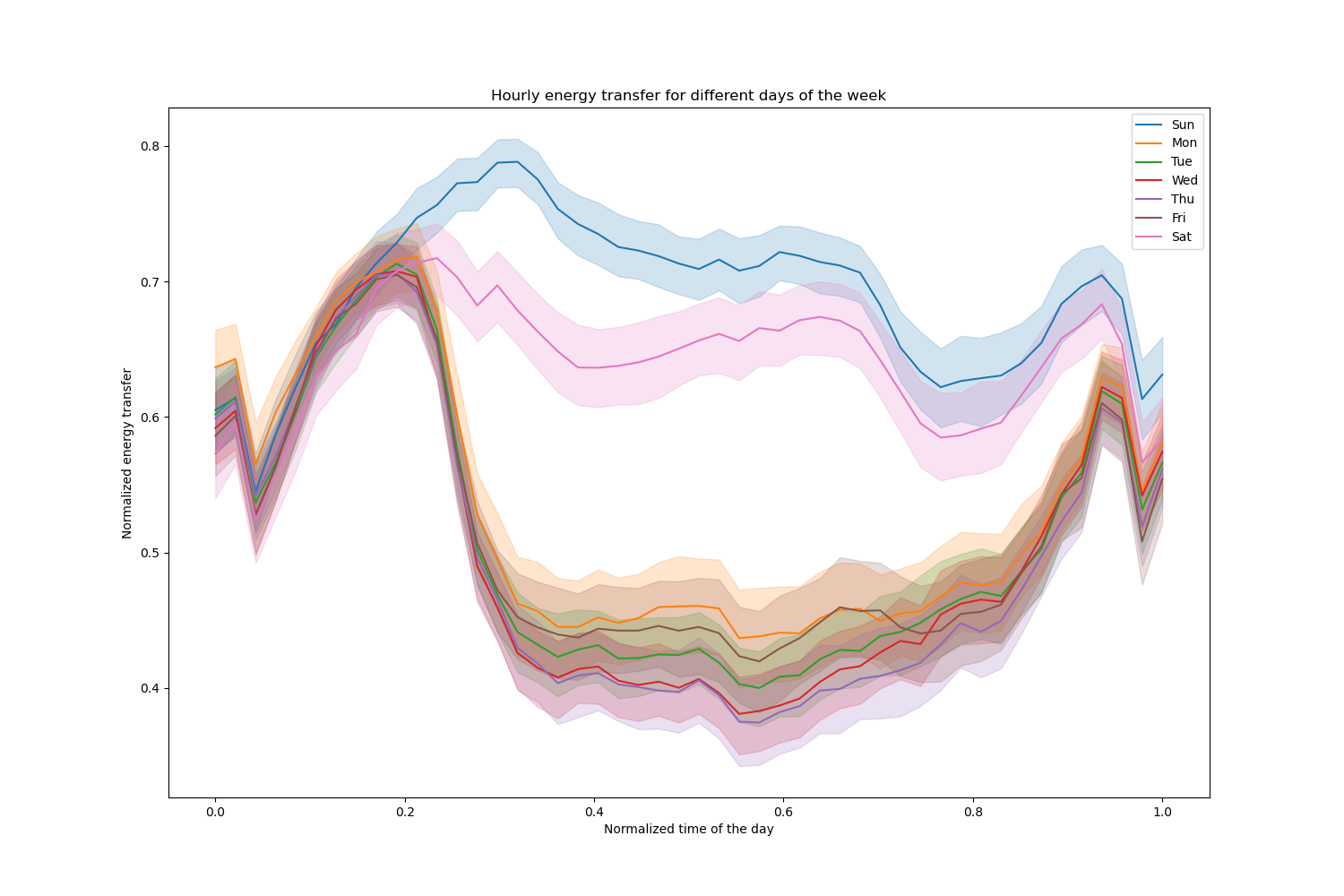
Beachten Sie, dass die Energieübertragung an Wochenenden systematisch zunimmt.
Auswirkungen der Anzahl der Bäume und des frühen Stoppens#
Um die Auswirkung der (maximalen) Anzahl der Bäume zu veranschaulichen, trainieren wir einen HistGradientBoostingRegressor über die tägliche Stromübertragung unter Verwendung des gesamten Datensatzes. Dann visualisieren wir seine Vorhersagen in Abhängigkeit vom Parameter max_iter. Hier versuchen wir nicht, die Leistung des Modells und seine Fähigkeit zur Generalisierung zu bewerten, sondern eher seine Fähigkeit, aus den Trainingsdaten zu lernen.
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, shuffle=False)
print(f"Training sample size: {X_train.shape[0]}")
print(f"Test sample size: {X_test.shape[0]}")
print(f"Number of features: {X_train.shape[1]}")
Training sample size: 16531
Test sample size: 11021
Number of features: 7
max_iter_list = [5, 50]
average_week_demand = (
df.loc[X_test.index].groupby(["day", "period"], observed=False)["transfer"].mean()
)
colors = sns.color_palette("colorblind")
fig, ax = plt.subplots(figsize=(10, 5))
average_week_demand.plot(color=colors[0], label="recorded average", linewidth=2, ax=ax)
for idx, max_iter in enumerate(max_iter_list):
hgbt = HistGradientBoostingRegressor(
max_iter=max_iter, categorical_features=None, random_state=42
)
hgbt.fit(X_train, y_train)
y_pred = hgbt.predict(X_test)
prediction_df = df.loc[X_test.index].copy()
prediction_df["y_pred"] = y_pred
average_pred = prediction_df.groupby(["day", "period"], observed=False)[
"y_pred"
].mean()
average_pred.plot(
color=colors[idx + 1], label=f"max_iter={max_iter}", linewidth=2, ax=ax
)
ax.set(
title="Predicted average energy transfer during the week",
xticks=[(i + 0.2) * 48 for i in range(7)],
xticklabels=["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"],
xlabel="Time of the week",
ylabel="Normalized energy transfer",
)
_ = ax.legend()
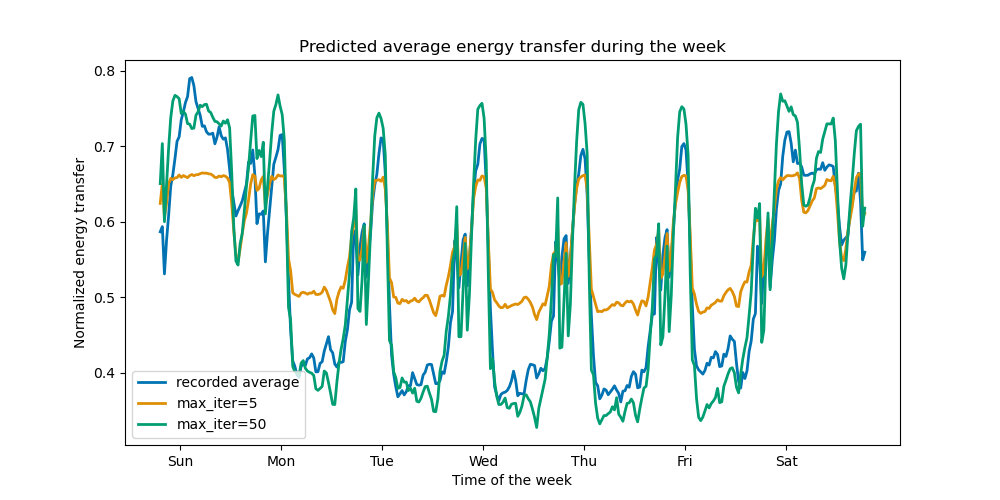
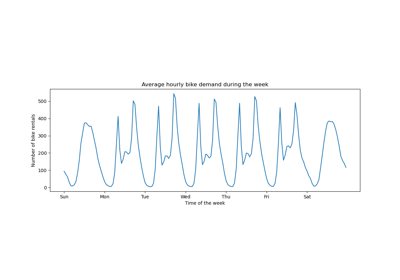
Mit nur wenigen Iterationen können HGBT-Modelle Konvergenz erreichen (siehe Vergleich von Random Forests und Histogramm Gradient Boosting Modellen), was bedeutet, dass das Hinzufügen weiterer Bäume das Modell nicht mehr verbessert. In der obigen Abbildung reichen 5 Iterationen nicht aus, um gute Vorhersagen zu erhalten. Mit 50 Iterationen können wir bereits eine gute Leistung erzielen.
Wenn max_iter zu hoch eingestellt ist, kann dies die Vorhersagequalität verschlechtern und viele unnötige Rechenressourcen verbrauchen. Daher bietet die HGBT-Implementierung in scikit-learn eine automatische Early Stopping-Strategie. Damit verwendet das Modell einen Bruchteil der Trainingsdaten als internen Validierungsdatensatz (validation_fraction) und stoppt das Training, wenn sich die Validierungsbewertung nach n_iter_no_change Iterationen bis zu einer bestimmten Toleranz (tol) nicht verbessert (oder verschlechtert).
Beachten Sie, dass es einen Kompromiss zwischen learning_rate und max_iter gibt: Generell sind kleinere Lernraten vorzuziehen, erfordern aber mehr Iterationen, um zum minimalen Verlust zu konvergieren, während größere Lernraten schneller konvergieren (weniger Iterationen/Bäume benötigt), aber auf Kosten eines größeren minimalen Verlusts.
Aufgrund dieser hohen Korrelation zwischen der Lernrate und der Anzahl der Iterationen ist es eine gute Praxis, die Lernrate zusammen mit allen (wichtigen) anderen Hyperparametern abzustimmen, das HBGT auf dem Trainingsdatensatz mit einem ausreichend großen Wert für max_iter anzupassen und das beste max_iter durch frühes Stoppen und eine explizite validation_fraction zu ermitteln.
common_params = {
"max_iter": 1_000,
"learning_rate": 0.3,
"validation_fraction": 0.2,
"random_state": 42,
"categorical_features": None,
"scoring": "neg_root_mean_squared_error",
}
hgbt = HistGradientBoostingRegressor(early_stopping=True, **common_params)
hgbt.fit(X_train, y_train)
_, ax = plt.subplots()
plt.plot(-hgbt.validation_score_)
_ = ax.set(
xlabel="number of iterations",
ylabel="root mean squared error",
title=f"Loss of hgbt with early stopping (n_iter={hgbt.n_iter_})",
)
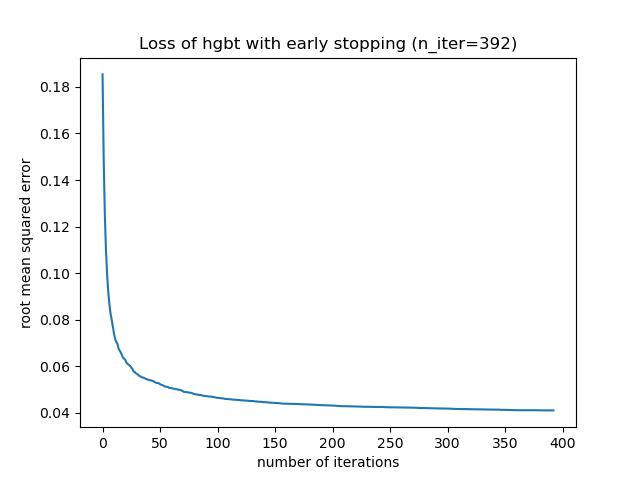
Wir können dann den Wert für max_iter auf einen vernünftigen Wert überschreiben und die zusätzlichen Rechenkosten der inneren Validierung vermeiden. Das Aufrunden der Anzahl der Iterationen kann die Variabilität des Trainingsdatensatzes berücksichtigen
import math
common_params["max_iter"] = math.ceil(hgbt.n_iter_ / 100) * 100
common_params["early_stopping"] = False
hgbt = HistGradientBoostingRegressor(**common_params)
Hinweis
Die innere Validierung, die während des frühen Stoppens durchgeführt wird, ist für Zeitreihen nicht optimal.
Unterstützung für fehlende Werte#
HGBT-Modelle haben eine native Unterstützung für fehlende Werte. Während des Trainings entscheidet der Baumzüchter, wohin Stichproben mit fehlenden Werten gehen sollen (linker oder rechter Kindknoten) bei jeder Teilung, basierend auf dem potenziellen Gewinn. Bei der Vorhersage werden diese Stichproben entsprechend zum gelernten Kindknoten geleitet. Wenn ein Merkmal während des Trainings keine fehlenden Werte hatte, werden für die Vorhersage Stichproben mit fehlenden Werten für dieses Merkmal zum Kindknoten mit den meisten Stichproben geleitet (wie bei der Anpassung beobachtet).
Das vorliegende Beispiel zeigt, wie HGBT-Regressionen mit vollständig zufällig fehlenden Werten (MCAR) umgehen, d.h. die Fehlenswerte hängen nicht von den beobachteten Daten oder den unbeobachteten Daten ab. Wir können ein solches Szenario simulieren, indem wir Werte aus zufällig ausgewählten Merkmalen zufällig durch nan-Werte ersetzen.
import numpy as np
from sklearn.metrics import root_mean_squared_error
rng = np.random.RandomState(42)
first_week = slice(0, 336) # first week in the test set as 7 * 48 = 336
missing_fraction_list = [0, 0.01, 0.03]
def generate_missing_values(X, missing_fraction):
total_cells = X.shape[0] * X.shape[1]
num_missing_cells = int(total_cells * missing_fraction)
row_indices = rng.choice(X.shape[0], num_missing_cells, replace=True)
col_indices = rng.choice(X.shape[1], num_missing_cells, replace=True)
X_missing = X.copy()
X_missing.iloc[row_indices, col_indices] = np.nan
return X_missing
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(y_test.values[first_week], label="Actual transfer")
for missing_fraction in missing_fraction_list:
X_train_missing = generate_missing_values(X_train, missing_fraction)
X_test_missing = generate_missing_values(X_test, missing_fraction)
hgbt.fit(X_train_missing, y_train)
y_pred = hgbt.predict(X_test_missing[first_week])
rmse = root_mean_squared_error(y_test[first_week], y_pred)
ax.plot(
y_pred[first_week],
label=f"missing_fraction={missing_fraction}, RMSE={rmse:.3f}",
alpha=0.5,
)
ax.set(
title="Daily energy transfer predictions on data with MCAR values",
xticks=[(i + 0.2) * 48 for i in range(7)],
xticklabels=["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"],
xlabel="Time of the week",
ylabel="Normalized energy transfer",
)
_ = ax.legend(loc="lower right")
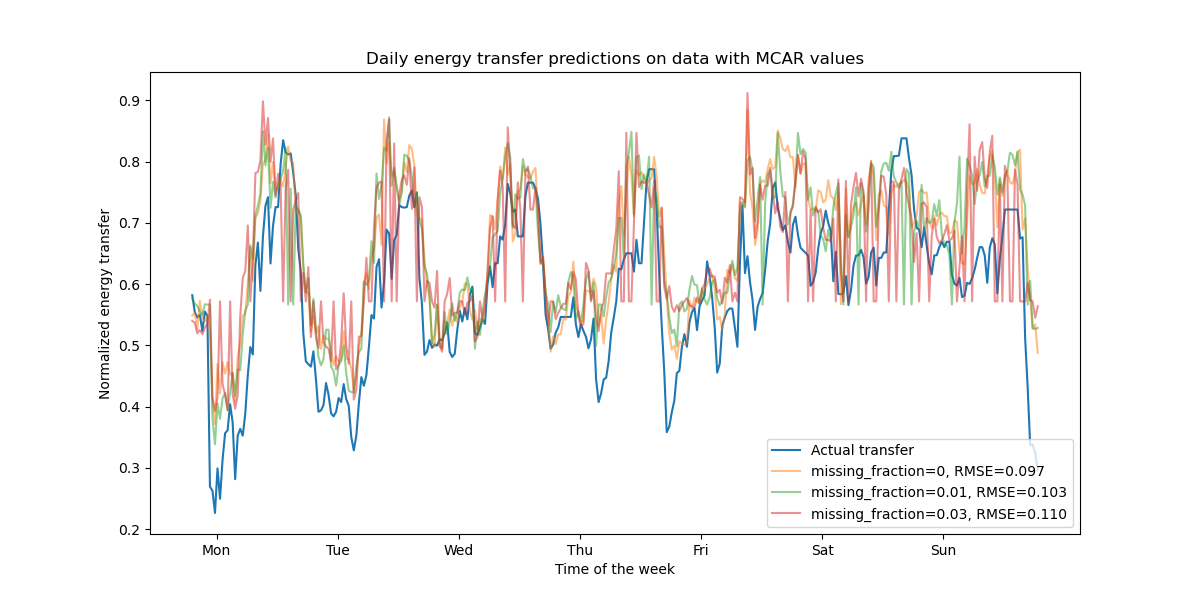
Wie erwartet verschlechtert sich das Modell mit zunehmendem Anteil fehlender Werte.
Unterstützung für Quantilverlust#
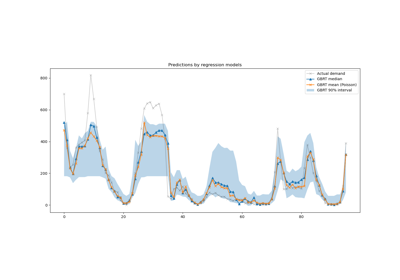
Der Quantilverlust in der Regression ermöglicht eine Betrachtung der Variabilität oder Unsicherheit der Zielvariablen. Zum Beispiel kann die Vorhersage des 5. und 95. Perzentils ein 90%iges Vorhersageintervall liefern, d.h. den Bereich, innerhalb dessen wir erwarten, dass ein neu beobachteter Wert mit 90%iger Wahrscheinlichkeit liegt.
from sklearn.metrics import mean_pinball_loss
quantiles = [0.95, 0.05]
predictions = []
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(y_test.values[first_week], label="Actual transfer")
for quantile in quantiles:
hgbt_quantile = HistGradientBoostingRegressor(
loss="quantile", quantile=quantile, **common_params
)
hgbt_quantile.fit(X_train, y_train)
y_pred = hgbt_quantile.predict(X_test[first_week])
predictions.append(y_pred)
score = mean_pinball_loss(y_test[first_week], y_pred)
ax.plot(
y_pred[first_week],
label=f"quantile={quantile}, pinball loss={score:.2f}",
alpha=0.5,
)
ax.fill_between(
range(len(predictions[0][first_week])),
predictions[0][first_week],
predictions[1][first_week],
color=colors[0],
alpha=0.1,
)
ax.set(
title="Daily energy transfer predictions with quantile loss",
xticks=[(i + 0.2) * 48 for i in range(7)],
xticklabels=["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"],
xlabel="Time of the week",
ylabel="Normalized energy transfer",
)
_ = ax.legend(loc="lower right")
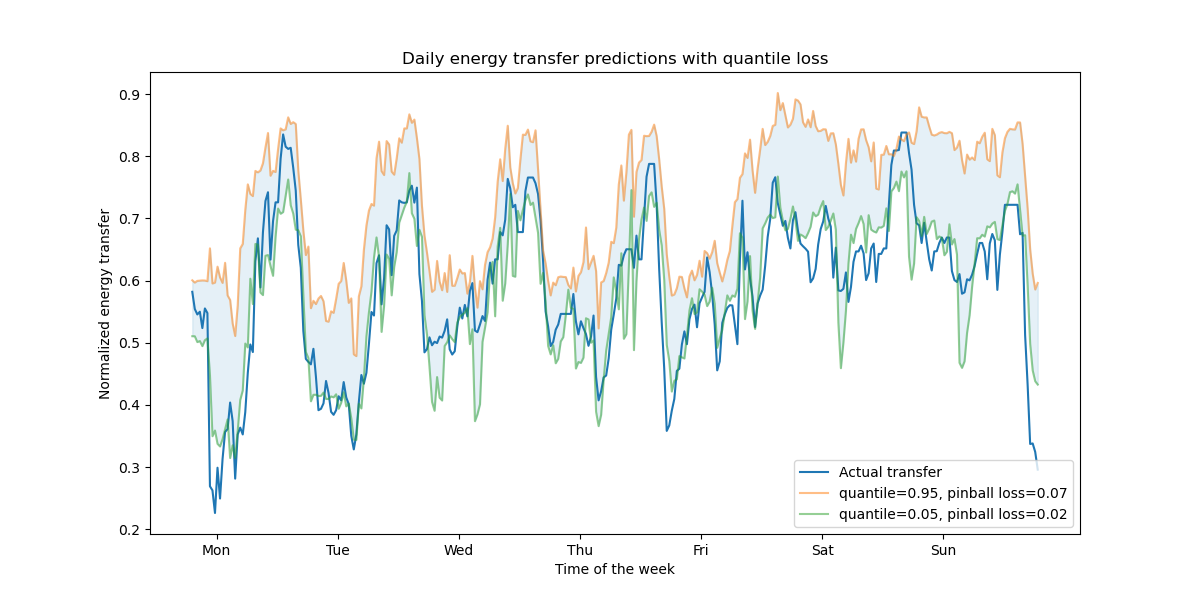
Wir beobachten eine Tendenz zur Überschätzung des Energieübertrags. Dies könnte quantitativ durch Berechnung empirischer Abdeckungszahlen bestätigt werden, wie im Abschnitt Kalibrierung von Konfidenzintervallen beschrieben. Beachten Sie, dass diese vorhergesagten Perzentile nur Schätzungen eines Modells sind. Man kann die Qualität solcher Schätzungen verbessern durch
Sammeln von mehr Datenpunkten;
besseres Abstimmen der Modellhyperparameter, siehe Vorhersageintervalle für Gradient Boosting Regression;
Erstellung aussagekräftigerer Merkmale aus denselben Daten, siehe Zeitbezogene Merkmal-Engineering.
Monotone Beschränkungen#
Bei spezifischem Domänenwissen, das erfordert, dass die Beziehung zwischen einem Merkmal und dem Ziel monoton steigend oder fallend ist, kann man dieses Verhalten in den Vorhersagen eines HGBT-Modells durch monotone Beschränkungen erzwingen. Dies macht das Modell interpretierbarer und kann seine Varianz reduzieren (und potenziell Überanpassung mildern) auf Kosten einer Erhöhung des Bias. Monotone Beschränkungen können auch verwendet werden, um spezifische regulatorische Anforderungen durchzusetzen, die Einhaltung zu gewährleisten und ethische Überlegungen zu berücksichtigen.
Im vorliegenden Beispiel soll die Politik der Energieübertragung von Victoria nach New South Wales Preisschwankungen lindern, was bedeutet, dass die Modellvorhersagen dieses Ziel erzwingen müssen, d.h. die Übertragung muss mit dem Preis und der Nachfrage in New South Wales steigen, aber auch mit dem Preis und der Nachfrage in Victoria sinken, um beiden Bevölkerungen zugute zu kommen.
Wenn die Trainingsdaten Merkmalsnamen haben, ist es möglich, die monotonen Beschränkungen anzugeben, indem ein Dictionary mit der Konvention übergeben wird
1: monoton steigend
0: keine Beschränkung
-1: monoton fallend
Alternativ kann ein Array-ähnliches Objekt übergeben werden, das die obige Konvention nach Position kodiert.
from sklearn.inspection import PartialDependenceDisplay
monotonic_cst = {
"date": 0,
"day": 0,
"period": 0,
"nswdemand": 1,
"nswprice": 1,
"vicdemand": -1,
"vicprice": -1,
}
hgbt_no_cst = HistGradientBoostingRegressor(
categorical_features=None, random_state=42
).fit(X, y)
hgbt_cst = HistGradientBoostingRegressor(
monotonic_cst=monotonic_cst, categorical_features=None, random_state=42
).fit(X, y)
fig, ax = plt.subplots(nrows=2, figsize=(15, 10))
disp = PartialDependenceDisplay.from_estimator(
hgbt_no_cst,
X,
features=["nswdemand", "nswprice"],
line_kw={"linewidth": 2, "label": "unconstrained", "color": "tab:blue"},
ax=ax[0],
)
PartialDependenceDisplay.from_estimator(
hgbt_cst,
X,
features=["nswdemand", "nswprice"],
line_kw={"linewidth": 2, "label": "constrained", "color": "tab:orange"},
ax=disp.axes_,
)
disp = PartialDependenceDisplay.from_estimator(
hgbt_no_cst,
X,
features=["vicdemand", "vicprice"],
line_kw={"linewidth": 2, "label": "unconstrained", "color": "tab:blue"},
ax=ax[1],
)
PartialDependenceDisplay.from_estimator(
hgbt_cst,
X,
features=["vicdemand", "vicprice"],
line_kw={"linewidth": 2, "label": "constrained", "color": "tab:orange"},
ax=disp.axes_,
)
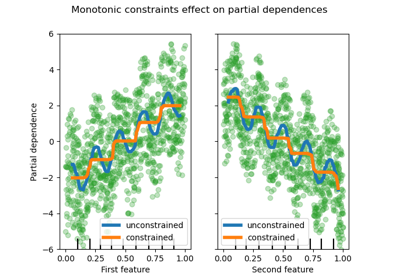
_ = plt.legend()
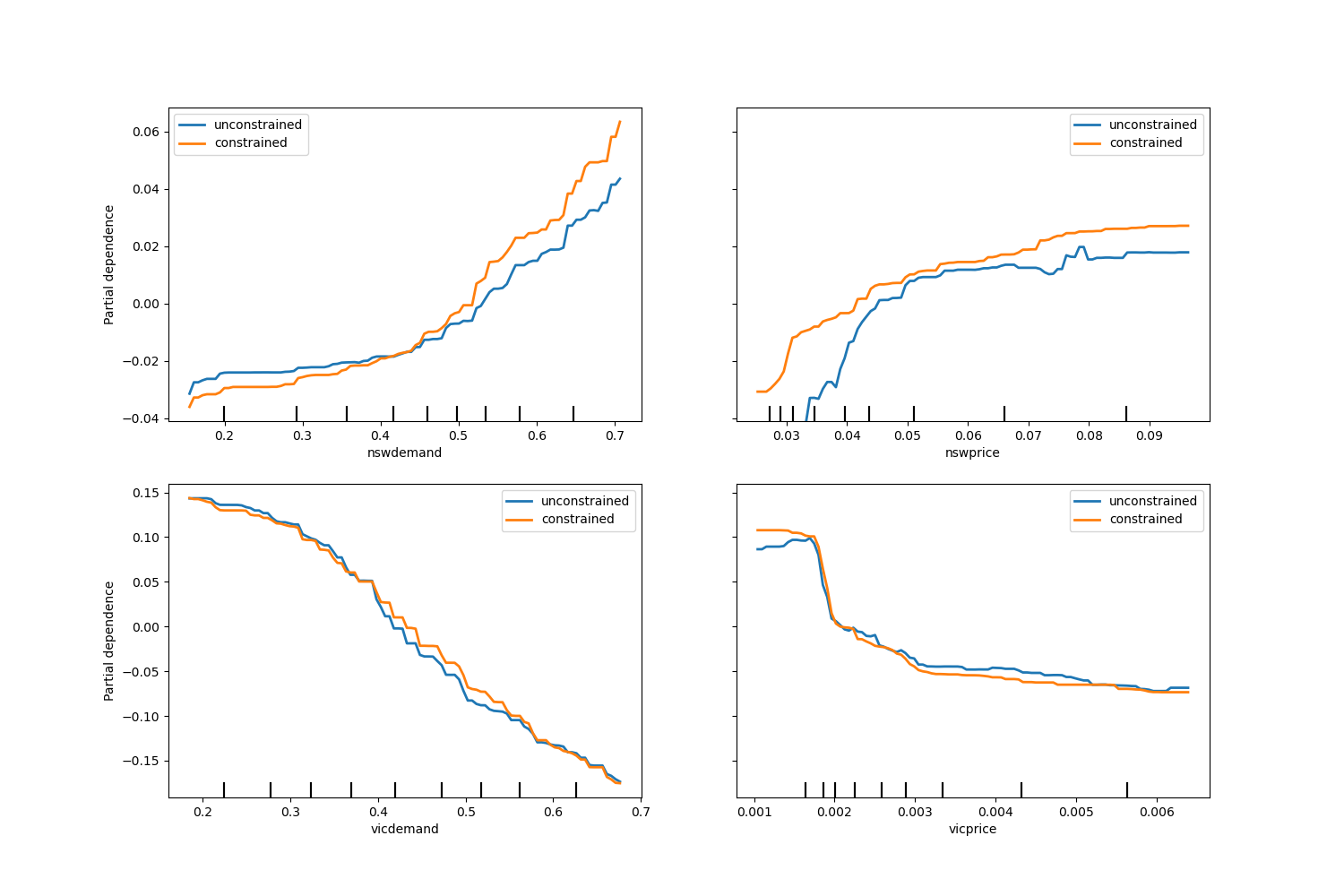
Beachten Sie, dass nswdemand und vicdemand bereits ohne Beschränkung monoton zu sein scheinen. Dies ist ein gutes Beispiel dafür, dass das Modell mit monotonen Beschränkungen „übermäßig einschränkend“ ist.
Zusätzlich können wir verifizieren, dass die Vorhersagequalität des Modells durch die Einführung monotoner Beschränkungen nicht signifikant beeinträchtigt wird. Zu diesem Zweck verwenden wir die TimeSeriesSplit-Kreuzvalidierung, um die Varianz der Testbewertung zu schätzen. Dadurch stellen wir sicher, dass die Trainingsdaten die Testdaten nicht überschreiten, was bei Daten mit einer zeitlichen Beziehung entscheidend ist.
from sklearn.metrics import make_scorer, root_mean_squared_error
from sklearn.model_selection import TimeSeriesSplit, cross_validate
ts_cv = TimeSeriesSplit(n_splits=5, gap=48, test_size=336) # a week has 336 samples
scorer = make_scorer(root_mean_squared_error)
cv_results = cross_validate(hgbt_no_cst, X, y, cv=ts_cv, scoring=scorer)
rmse = cv_results["test_score"]
print(f"RMSE without constraints = {rmse.mean():.3f} +/- {rmse.std():.3f}")
cv_results = cross_validate(hgbt_cst, X, y, cv=ts_cv, scoring=scorer)
rmse = cv_results["test_score"]
print(f"RMSE with constraints = {rmse.mean():.3f} +/- {rmse.std():.3f}")
RMSE without constraints = 0.103 +/- 0.030
RMSE with constraints = 0.107 +/- 0.034
Das bedeutet, dass der Vergleich zwischen zwei verschiedenen Modellen stattfindet, die möglicherweise durch eine andere Kombination von Hyperparametern optimiert wurden. Aus diesem Grund verwenden wir in diesem Abschnitt nicht die common_params, wie zuvor.
Gesamtlaufzeit des Skripts: (0 Minuten 18,194 Sekunden)
Verwandte Beispiele

Vergleich von Random Forests und Histogram Gradient Boosting Modellen