1.11. Ensembles: Gradienten-Boosting, Random Forests, Bagging, Voting, Stacking#

Ensemble-Methoden kombinieren die Vorhersagen mehrerer Basis-Schätzer, die mit einem gegebenen Lernalgorithmus erstellt wurden, um die Generalisierbarkeit/Robustheit gegenüber einem einzelnen Schätzer zu verbessern.

Zwei sehr bekannte Beispiele für Ensemble-Methoden sind Gradienten-Boosted Trees und Random Forests.

Allgemeiner können Ensemble-Modelle auf jeden Basis-Lerner über Bäume hinaus angewendet werden, in Mittelwertbildungsmethoden wie Bagging-Methoden, Model Stacking oder Voting, oder im Boosting, wie AdaBoost.

1.11.1. Gradienten-Boosted Trees#

Gradient Tree Boosting oder Gradient Boosted Decision Trees (GBDT) ist eine Verallgemeinerung des Boostings auf beliebige differenzierbare Verlustfunktionen, siehe die wegweisende Arbeit von [Friedman2001]. GBDT ist ein exzellentes Modell für Regression und Klassifikation, insbesondere für tabellarische Daten.

1.11.1.1. Histogramm-basierte Gradienten-Boostung#

Scikit-learn 0.21 führte zwei neue Implementierungen von Gradienten-Boosted Trees ein, nämlich HistGradientBoostingClassifier und HistGradientBoostingRegressor, inspiriert von LightGBM (siehe [LightGBM]).

Diese histogramm-basierten Schätzer können um Größenordnungen schneller sein als GradientBoostingClassifier und GradientBoostingRegressor, wenn die Anzahl der Samples größer als Zehntausende ist.

Sie verfügen auch über integrierte Unterstützung für fehlende Werte, wodurch die Notwendigkeit eines Imputers entfällt.

Diese schnellen Schätzer bündeln zunächst die Eingabestichproben X in ganzzahlige Bins (typischerweise 256 Bins), was die Anzahl der zu berücksichtigenden Aufteilungspunkte drastisch reduziert und es dem Algorithmus ermöglicht, ganzzahlige Datenstrukturen (Histogramme) zu nutzen, anstatt sich beim Aufbau der Bäume auf sortierte kontinuierliche Werte zu verlassen. Die API dieser Schätzer ist leicht unterschiedlich, und einige Funktionen von GradientBoostingClassifier und GradientBoostingRegressor werden noch nicht unterstützt, zum Beispiel einige Verlustfunktionen.

Beispiele

1.11.1.1.1. Verwendung#

Die meisten Parameter sind unverändert gegenüber GradientBoostingClassifier und GradientBoostingRegressor. Eine Ausnahme bildet der Parameter max_iter, der n_estimators ersetzt und die Anzahl der Iterationen des Boosting-Prozesses steuert.

>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> from sklearn.datasets import make_hastie_10_2

>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]

>>> clf = HistGradientBoostingClassifier(max_iter=100).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.8965

Verfügbare Verluste für Regression sind:

‘squared_error’, der Standardverlust;
‘absolute_error’, der weniger empfindlich auf Ausreißer reagiert als der quadratische Fehler;
‘gamma’, der gut geeignet ist, um streng positive Ergebnisse zu modellieren;
‘poisson’, der gut geeignet ist, um Zählungen und Frequenzen zu modellieren;
‘quantile’, der die Schätzung eines bedingten Quantils ermöglicht, das später zur Ermittlung von Vorhersageintervallen verwendet werden kann.

Für Klassifikation ist ‘log_loss’ die einzige Option. Für binäre Klassifikation wird der binäre Log-Verlust verwendet, auch bekannt als binomiale Devianz oder binäre Kreuzentropie. Für n_classes >= 3 wird die multiklassen-Log-Verlustfunktion verwendet, mit multinominaler Devianz und kategorialer Kreuzentropie als alternative Namen. Die geeignete Verlustversion wird basierend auf y, das an fit übergeben wird, ausgewählt.

Die Größe der Bäume kann über die Parameter max_leaf_nodes, max_depth und min_samples_leaf gesteuert werden.

Die Anzahl der zur Bündelung der Daten verwendeten Bins wird mit dem Parameter max_bins gesteuert. Die Verwendung weniger Bins wirkt als eine Form der Regularisierung. Es wird generell empfohlen, so viele Bins wie möglich zu verwenden (255), was der Standard ist.

Der Parameter l2_regularization fungiert als Regularisator für die Verlustfunktion und entspricht \(\lambda\) in der folgenden Gleichung (siehe Gleichung (2) in [XGBoost])

\[\mathcal{L}(\phi) = \sum_i l(\hat{y}_i, y_i) + \frac12 \sum_k \lambda ||w_k||^2\]

Beachten Sie, dass Early-Stopping standardmäßig aktiviert ist, wenn die Anzahl der Samples größer als 10.000 ist. Das Verhalten von Early-Stopping wird über die Parameter early_stopping, scoring, validation_fraction, n_iter_no_change und tol gesteuert. Es ist möglich, mit einem beliebigen Scorer oder nur dem Trainings- oder Validierungsverlust ein Early-Stopping durchzuführen. Beachten Sie, dass die Verwendung eines aufrufbaren Scorer aus technischen Gründen deutlich langsamer ist als die Verwendung des Verlusts. Standardmäßig wird Early-Stopping durchgeführt, wenn mindestens 10.000 Samples im Trainingsset vorhanden sind, wobei der Validierungsverlust verwendet wird.

1.11.1.1.2. Unterstützung für fehlende Werte#

HistGradientBoostingClassifier und HistGradientBoostingRegressor verfügen über integrierte Unterstützung für fehlende Werte (NaNs).

Während des Trainings lernt der Baum-Erzeuger an jedem Aufteilungspunkt, ob Samples mit fehlenden Werten zum linken oder rechten Kind gehen sollen, basierend auf dem potenziellen Gewinn. Bei der Vorhersage werden Samples mit fehlenden Werten entsprechend zum linken oder rechten Kind zugewiesen.

>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> import numpy as np

>>> X = np.array([0, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]

>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 0, 1, 1])

Wenn die Muster der fehlenden Werte prädiktiv sind, können die Aufteilungen auf Basis der Tatsache erfolgen, ob der Merkmalswert fehlt oder nicht.

>>> X = np.array([0, np.nan, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 1, 0, 0, 1]
>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1,
...                                       max_depth=2,
...                                       learning_rate=1,
...                                       max_iter=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 1, 0, 0, 1])

Wenn während des Trainings keine fehlenden Werte für ein bestimmtes Merkmal angetroffen wurden, werden Samples mit fehlenden Werten dem Kindknoten zugeordnet, der die meisten Samples enthält.

Beispiele

Merkmale in Histogram Gradient Boosting Bäumen

1.11.1.1.3. Unterstützung für Sample-Gewichte#

HistGradientBoostingClassifier und HistGradientBoostingRegressor unterstützen Sample-Gewichte während fit.

Das folgende Beispiel zeigt, dass Samples mit einem Sample-Gewicht von Null ignoriert werden.

>>> X = [[1, 0],
...      [1, 0],
...      [1, 0],
...      [0, 1]]
>>> y = [0, 0, 1, 0]
>>> # ignore the first 2 training samples by setting their weight to 0
>>> sample_weight = [0, 0, 1, 1]
>>> gb = HistGradientBoostingClassifier(min_samples_leaf=1)
>>> gb.fit(X, y, sample_weight=sample_weight)
HistGradientBoostingClassifier(...)
>>> gb.predict([[1, 0]])
array([1])
>>> gb.predict_proba([[1, 0]])[0, 1]
np.float64(0.999)

Wie Sie sehen können, wird [1, 0] komfortabel als 1 klassifiziert, da die ersten beiden Samples aufgrund ihrer Sample-Gewichte ignoriert werden.

Implementierungsdetails: Die Berücksichtigung von Sample-Gewichten entspricht der Multiplikation der Gradienten (und der Hessemann) mit den Sample-Gewichten. Beachten Sie, dass die Binning-Phase (insbesondere die Quantilsberechnung) die Gewichte nicht berücksichtigt.

1.11.1.1.4. Unterstützung für kategoriale Merkmale#

HistGradientBoostingClassifier und HistGradientBoostingRegressor haben eine native Unterstützung für kategoriale Merkmale: sie können Aufteilungen auf nicht-geordnete, kategoriale Daten berücksichtigen.

Für Datensätze mit kategorialen Merkmalen ist die Verwendung der nativen kategorialen Unterstützung oft besser als die Verwendung von One-Hot-Encoding (OneHotEncoder), da One-Hot-Encoding mehr Baumtiefe benötigt, um äquivalente Aufteilungen zu erreichen. Es ist auch normalerweise besser, sich auf die native kategoriale Unterstützung zu verlassen, anstatt kategoriale Merkmale als kontinuierlich (ordinal) zu behandeln, was bei ordinal kodierten kategorialen Daten geschieht, da Kategorien nominale Größen sind, bei denen die Reihenfolge keine Rolle spielt.

Um die kategoriale Unterstützung zu aktivieren, kann eine boolesche Maske an den Parameter categorical_features übergeben werden, die angibt, welches Merkmal kategorial ist. Im Folgenden wird das erste Merkmal als kategorial und das zweite Merkmal als numerisch behandelt.

>>> gbdt = HistGradientBoostingClassifier(categorical_features=[True, False])

Gleichwertig kann eine Liste von Ganzzahlen übergeben werden, die die Indizes der kategorialen Merkmale angeben.

>>> gbdt = HistGradientBoostingClassifier(categorical_features=[0])

Wenn die Eingabe ein DataFrame ist, ist es auch möglich, eine Liste von Spaltennamen zu übergeben.

>>> gbdt = HistGradientBoostingClassifier(categorical_features=["site", "manufacturer"])

Schließlich, wenn die Eingabe ein DataFrame ist, können wir categorical_features="from_dtype" verwenden, in diesem Fall werden alle Spalten mit einem kategorialen dtype als kategoriale Merkmale behandelt.

Die Kardinalität jedes kategorialen Merkmals muss kleiner sein als der Parameter max_bins. Ein Beispiel für die Verwendung von histogramm-basierter Gradienten-Boostung auf kategorialen Merkmalen finden Sie unter Unterstützung kategorialer Merkmale in Gradient Boosting.

Wenn während des Trainings fehlende Werte vorhanden sind, werden diese als eigene Kategorie behandelt. Wenn während des Trainings keine fehlenden Werte vorhanden sind, werden bei der Vorhersage fehlende Werte dem Kindknoten zugeordnet, der die meisten Samples enthält (genauso wie bei kontinuierlichen Merkmalen). Bei der Vorhersage werden Kategorien, die während des Fits nicht gesehen wurden, als fehlende Werte behandelt.

Beispiele

Unterstützung für kategorische Merkmale in Gradient Boosting

1.11.1.1.5. Monotone Einschränkungen#

Abhängig vom Problem können Sie Vorwissen haben, das darauf hindeutet, dass ein bestimmtes Merkmal im Allgemeinen einen positiven (oder negativen) Einfluss auf den Zielwert haben sollte. Zum Beispiel sollte ein höherer Kredit-Score, alles andere gleich, die Wahrscheinlichkeit erhöhen, für ein Darlehen zugelassen zu werden. Monotone Einschränkungen ermöglichen es Ihnen, solches Vorwissen in das Modell zu integrieren.

Für einen Prädiktor \(F\) mit zwei Merkmalen

ist eine monoton steigende Einschränkung eine Einschränkung der Form

\[x_1 \leq x_1' \implies F(x_1, x_2) \leq F(x_1', x_2)\]
und eine monoton fallende Einschränkung ist eine Einschränkung der Form

\[x_1 \leq x_1' \implies F(x_1, x_2) \geq F(x_1', x_2)\]

Sie können eine monotone Einschränkung für jedes Merkmal über den Parameter monotonic_cst festlegen. Für jedes Merkmal bedeutet ein Wert von 0 keine Einschränkung, während 1 und -1 eine monotone Steigerungs- bzw. Abnahmeeinschränkung bedeuten.

>>> from sklearn.ensemble import HistGradientBoostingRegressor

... # monotonic increase, monotonic decrease, and no constraint on the 3 features
>>> gbdt = HistGradientBoostingRegressor(monotonic_cst=[1, -1, 0])

Im Kontext der binären Klassifikation bedeutet die Anwendung einer monoton steigenden (fallenden) Einschränkung, dass höhere Werte des Merkmals einen positiven (negativen) Einfluss auf die Wahrscheinlichkeit der Zugehörigkeit von Samples zur positiven Klasse haben sollen.

Dennoch schränken monotone Einschränkungen die Merkmalseffekte auf die Ausgabe nur marginal ein. Zum Beispiel können monotone Steigerungs- und Abnahmeeinschränkungen nicht verwendet werden, um die folgende Modellierungseinschränkung zu erzwingen:

\[x_1 \leq x_1' \implies F(x_1, x_2) \leq F(x_1', x_2')\]

Außerdem werden monotone Einschränkungen für die Multiklassen-Klassifikation nicht unterstützt.

Für eine praktische Implementierung von monotonen Einschränkungen mit der histogramm-basierten Gradienten-Boostung, einschließlich wie sie die Generalisierung bei verfügbarem Domänenwissen verbessern können, siehe Monotone Einschränkungen.

Hinweis

Da Kategorien ungeordnete Größen sind, ist es nicht möglich, monotone Einschränkungen für kategoriale Merkmale zu erzwingen.

Beispiele

Merkmale in Histogram Gradient Boosting Bäumen

1.11.1.1.6. Interaktionsbeschränkungen#

A priori dürfen die histogramm-basierten Gradienten-Boosted Trees jedes Merkmal verwenden, um einen Knoten in Kindknoten aufzuteilen. Dies erzeugt sogenannte Wechselwirkungen zwischen Merkmalen, d. h. die Verwendung unterschiedlicher Merkmale als Aufteilung entlang eines Zweiges. Manchmal möchte man die möglichen Wechselwirkungen einschränken, siehe [Mayer2022]. Dies kann durch den Parameter interaction_cst geschehen, bei dem die Indizes der Merkmale angegeben werden können, die miteinander interagieren dürfen. Beispielsweise verbietet bei insgesamt 3 Merkmalen interaction_cst=[{0}, {1}, {2}] alle Wechselwirkungen. Die Einschränkungen [{0, 1}, {1, 2}] spezifizieren zwei Gruppen von möglicherweise interagierenden Merkmalen. Merkmale 0 und 1 können miteinander interagieren, ebenso wie Merkmale 1 und 2. Beachten Sie jedoch, dass die Merkmale 0 und 2 nicht miteinander interagieren dürfen. Das Folgende veranschaulicht einen Baum und die möglichen Aufteilungen des Baumes.

   1      <- Both constraint groups could be applied from now on
  / \
 1   2    <- Left split still fulfills both constraint groups.
/ \ / \      Right split at feature 2 has only group {1, 2} from now on.

LightGBM verwendet die gleiche Logik für überlappende Gruppen.

Beachten Sie, dass Merkmale, die nicht in interaction_cst aufgeführt sind, automatisch eine eigene Interaktionsgruppe erhalten. Bei wieder 3 Merkmalen bedeutet dies, dass [{0}] äquivalent zu [{0}, {1, 2}] ist.

Beispiele

Partial Dependence und Individual Conditional Expectation Plots

Referenzen

[Mayer2022]

M. Mayer, S.C. Bourassa, M. Hoesli, und D.F. Scognamiglio. 2022. Machine Learning Applications to Land and Structure Valuation. Journal of Risk and Financial Management 15, Nr. 5: 193

1.11.1.1.7. Low-Level-Parallelität#

HistGradientBoostingClassifier und HistGradientBoostingRegressor verwenden OpenMP für die Parallelisierung über Cython. Weitere Details zur Steuerung der Anzahl von Threads finden Sie in unseren Hinweisen zur Parallelität.

Die folgenden Teile werden parallelisiert:

Zuordnung von Samples von reellen Werten zu ganzzahligen Bins (die Bestimmung der Bin-Schwellenwerte ist jedoch sequenziell)
Aufbau von Histogrammen, parallelisiert über Merkmale
Bestimmung des besten Aufteilungspunkts an einem Knoten, parallelisiert über Merkmale
während des Fits, Zuordnung von Samples zu den linken und rechten Kindern, parallelisiert über Samples
Berechnung von Gradienten und Hessemann, parallelisiert über Samples
Vorhersage, parallelisiert über Samples

1.11.1.1.8. Warum es schneller ist#

Der Engpass eines Gradienten-Boosting-Verfahrens ist der Aufbau der Entscheidungsbäume. Der Aufbau eines traditionellen Entscheidungsbaums (wie in den anderen GBDTs GradientBoostingClassifier und GradientBoostingRegressor) erfordert das Sortieren der Samples an jedem Knoten (für jedes Merkmal). Sortieren ist notwendig, damit der potenzielle Gewinn eines Aufteilungspunkts effizient berechnet werden kann. Das Aufteilen eines einzelnen Knotens hat somit eine Komplexität von \(\mathcal{O}(n_\text{features} \times n \log(n))\), wobei \(n\) die Anzahl der Samples am Knoten ist.

HistGradientBoostingClassifier und HistGradientBoostingRegressor hingegen erfordern kein Sortieren der Merkmalswerte und verwenden stattdessen eine Datenstruktur namens Histogramm, bei der die Samples implizit geordnet sind. Der Aufbau eines Histogramms hat eine Komplexität von \(\mathcal{O}(n)\), sodass das Verfahren zur Aufteilung von Knoten eine Komplexität von \(\mathcal{O}(n_\text{features} \times n)\) hat, was deutlich kleiner ist als die vorherige. Zusätzlich werden anstelle von \(n\) Aufteilungspunkten nur max_bins Aufteilungspunkte betrachtet, was deutlich weniger sein kann.

Um Histogramme zu erstellen, müssen die Eingabedaten X in ganzzahlige Bins umgewandelt werden. Dieses Binning-Verfahren erfordert zwar das Sortieren der Merkmalswerte, aber es geschieht nur einmal am Anfang des Boosting-Prozesses (nicht an jedem Knoten, wie bei GradientBoostingClassifier und GradientBoostingRegressor).

Schließlich sind viele Teile der Implementierung von HistGradientBoostingClassifier und HistGradientBoostingRegressor parallelisiert.

Referenzen

[XGBoost] (1,2,3)

Tianqi Chen, Carlos Guestrin, „XGBoost: A Scalable Tree Boosting System“

[LightGBM]

Ke et. al. „LightGBM: A Highly Efficient Gradient Boosting Decision Tree“

[Fisher1958]

Fisher, W.D. (1958). „On Grouping for Maximum Homogeneity“ Journal of the American Statistical Association, 53, 789-798.

1.11.1.2. `GradientBoostingClassifier` und `GradientBoostingRegressor`#

Die Verwendung und die Parameter von GradientBoostingClassifier und GradientBoostingRegressor werden unten beschrieben. Die 2 wichtigsten Parameter dieser Schätzer sind n_estimators und learning_rate.

Beispiele

1.11.1.2.1. Anpassen zusätzlicher schwacher Lerner#

GradientBoostingRegressor und GradientBoostingClassifier unterstützen beide warm_start=True, was es Ihnen ermöglicht, einem bereits angepassten Modell weitere Schätzer hinzuzufügen.

>>> import numpy as np
>>> from sklearn.metrics import mean_squared_error
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor

>>> X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
>>> X_train, X_test = X[:200], X[200:]
>>> y_train, y_test = y[:200], y[200:]
>>> est = GradientBoostingRegressor(
...     n_estimators=100, learning_rate=0.1, max_depth=1, random_state=0,
...     loss='squared_error'
... )
>>> est = est.fit(X_train, y_train)  # fit with 100 trees
>>> mean_squared_error(y_test, est.predict(X_test))
5.00
>>> _ = est.set_params(n_estimators=200, warm_start=True)  # set warm_start and increase num of trees
>>> _ = est.fit(X_train, y_train) # fit additional 100 trees to est
>>> mean_squared_error(y_test, est.predict(X_test))
3.84

1.11.1.2.2. Steuerung der Baumgröße#

Die Größe der Regressionsbaum-Basis-Lerner bestimmt die Ebene der Variableninteraktionen, die vom Gradient-Boosting-Modell erfasst werden können. Im Allgemeinen kann ein Baum der Tiefe h Interaktionen der Ordnung h erfassen. Es gibt zwei Möglichkeiten, die Größe der einzelnen Regressionsbäume zu steuern.

Wenn Sie max_depth=h angeben, werden vollständige Binärbäume der Tiefe h aufgebaut. Solche Bäume haben (höchstens) 2**h Blattknoten und 2**h - 1 Aufteilungsknoten.

Alternativ können Sie die Baumgröße steuern, indem Sie die Anzahl der Blattknoten über den Parameter max_leaf_nodes angeben. In diesem Fall werden die Bäume mit einer Best-First-Suche aufgebaut, wobei zuerst Knoten mit der höchsten Verbesserung der Unreinheit erweitert werden. Ein Baum mit max_leaf_nodes=k hat k - 1 Aufteilungsknoten und kann daher Interaktionen bis zur Ordnung max_leaf_nodes - 1 modellieren.

Wir haben festgestellt, dass max_leaf_nodes=k vergleichbare Ergebnisse wie max_depth=k-1 liefert, aber signifikant schneller trainiert, auf Kosten eines geringfügig höheren Trainingsfehlers. Der Parameter max_leaf_nodes entspricht der Variablen J im Kapitel über Gradient Boosting in [Friedman2001] und steht im Zusammenhang mit dem Parameter interaction.depth im R-Paket gbm, wobei max_leaf_nodes == interaction.depth + 1 gilt.

1.11.1.2.3. Mathematische Formulierung#

Wir präsentieren zunächst GBRT für Regression und gehen dann auf den Klassifikationsfall ein.

Regression#

GBRT-Regressoren sind additive Modelle, deren Vorhersage \(\hat{y}_i\) für einen gegebenen Eingabewert \(x_i\) folgende Form hat

\[\hat{y}_i = F_M(x_i) = \sum_{m=1}^{M} h_m(x_i)\]

wobei die \(h_m\) Schätzer sind, die im Kontext von Boosting als schwache Lerner bezeichnet werden. Gradient Tree Boosting verwendet Entscheidungsbaum-Regressoren fester Größe als schwache Lerner. Die Konstante M entspricht dem Parameter n_estimators.

Ähnlich wie andere Boosting-Algorithmen wird ein GBRT in einem gierigen Verfahren aufgebaut

\[F_m(x) = F_{m-1}(x) + h_m(x),\]

wobei der neu hinzugefügte Baum \(h_m\) so angepasst wird, dass er eine Summe von Verlusten \(\boldsymbol{L}_m\) minimiert, gegeben das vorherige Ensemble \(\boldsymbol{F}_{\boldsymbol{m}-1}\)

\[h_m = \arg\min_{h} L_m = \arg\min_{h} \sum_{i=1}^{n} l(y_i, F_{m-1}(x_i) + h(x_i)),\]

wobei \(l(y_i, F(x_i))\) durch den Parameter loss definiert ist, der im nächsten Abschnitt näher erläutert wird.

Standardmäßig wird das Anfangsmodell \(\boldsymbol{F}_{\boldsymbol{0}}\) als die Konstante gewählt, die den Verlust minimiert: für eine Verlustfunktion der kleinsten Quadrate ist dies der empirische Mittelwert der Zielwerte. Das Anfangsmodell kann auch über das Argument init angegeben werden.

Unter Verwendung einer Taylor-Näherung erster Ordnung kann der Wert von \(\boldsymbol{l}\) wie folgt angenähert werden

\[l(y_i, F_{m-1}(x_i) + h_m(x_i)) \approx l(y_i, F_{m-1}(x_i)) + h_m(x_i) \left[ \frac{\partial l(y_i, F(x_i))}{\partial F(x_i)} \right]_{F=F_{m - 1}}.\]

Hinweis

Kurz gesagt besagt eine Taylor-Näherung erster Ordnung, dass \(\boldsymbol{l}(\boldsymbol{z}) \approx \boldsymbol{l}(\boldsymbol{a}) + (\boldsymbol{z} - \boldsymbol{a}) \frac{\partial \boldsymbol{l}}{\partial \boldsymbol{z}}(\boldsymbol{a})\). Hier entspricht \(\boldsymbol{z}\) \(\boldsymbol{F}_{\boldsymbol{m} - \boldsymbol{1}}(\boldsymbol{x}_{\boldsymbol{i}}) + \boldsymbol{h}_{\boldsymbol{m}}(\boldsymbol{x}_{\boldsymbol{i}})\) und \(\boldsymbol{a}\) entspricht \(\boldsymbol{F}_{\boldsymbol{m}-1}(\boldsymbol{x}_{\boldsymbol{i}})\).

Die Größe \(\left[ \frac{\partial l(y_i, F(x_i))}{\partial F(x_i)} \right]_{F=F_{m - 1}}\) ist die Ableitung des Verlusts nach seinem zweiten Parameter, ausgewertet an \(\boldsymbol{F}_{\boldsymbol{m}-1}(\boldsymbol{x})\). Sie ist leicht für jedes gegebene \(\boldsymbol{F}_{\boldsymbol{m} - \boldsymbol{1}}(\boldsymbol{x}_{\boldsymbol{i}})\) in geschlossener Form berechenbar, da der Verlust differenzierbar ist. Wir werden ihn mit \(\boldsymbol{g}_{\boldsymbol{i}}\) bezeichnen.

Wenn wir die konstanten Terme entfernen, haben wir

\[h_m \approx \arg\min_{h} \sum_{i=1}^{n} h(x_i) g_i\]

Dies wird minimiert, wenn \(\boldsymbol{h}(\boldsymbol{x}_{\boldsymbol{i}})\) so angepasst wird, dass es proportional zum negativen Gradienten \(\boldsymbol{-g}_{\boldsymbol{i}}\) vorhersagt. Daher wird bei jeder Iteration der Schätzer \(\boldsymbol{h}_{\boldsymbol{m}}\) so angepasst, dass er die negativen Gradienten der Stichproben vorhersagt. Die Gradienten werden bei jeder Iteration aktualisiert. Dies kann als eine Art Gradientenabstieg in einem Funktionsraum betrachtet werden.

Hinweis

Für einige Verlustfunktionen, z. B. 'absolute_error', bei der die Gradienten \(\pm 1\) sind, sind die von einem angepassten \(\boldsymbol{h}_{\boldsymbol{m}}\) vorhergesagten Werte nicht genau genug: der Baum kann nur ganzzahlige Werte ausgeben. Infolgedessen werden die Blattwerte des Baumes \(\boldsymbol{h}_{\boldsymbol{m}}\) nach der Anpassung modifiziert, so dass die Blattwerte den Verlust \(\boldsymbol{L}_{\boldsymbol{m}}\) minimieren. Die Aktualisierung ist verlustabhängig: für die absolute Fehlerverlustfunktion wird der Wert eines Blattes auf den Median der Stichproben in diesem Blatt aktualisiert.

1.11.1.2.4. Verlustfunktionen#

Die folgenden Verlustfunktionen werden unterstützt und können über den Parameter loss angegeben werden:

1.11.1.2.5. Schrumpfung durch Lernrate#

[Friedman2001] schlug eine einfache Regularisierungsstrategie vor, die den Beitrag jedes schwachen Lerners um einen konstanten Faktor \(\nu\) skaliert

\[F_m(x) = F_{m-1}(x) + \nu h_m(x)\]

Der Parameter \(\nu\) wird auch als Lernrate bezeichnet, da er die Schrittlänge des Gradientenabstiegsverfahrens skaliert; er kann über den Parameter learning_rate gesetzt werden.

Der Parameter learning_rate interagiert stark mit dem Parameter n_estimators, der Anzahl der anzupassenden schwachen Lerner. Kleinere Werte für learning_rate erfordern größere Anzahlen schwacher Lerner, um einen konstanten Trainingsfehler aufrechtzuerhalten. Empirische Beweise deuten darauf hin, dass kleine Werte von learning_rate einen besseren Testfehler begünstigen. [HTF] empfehlen, die Lernrate auf eine kleine Konstante zu setzen (z. B. learning_rate <= 0.1) und n_estimators groß genug zu wählen, dass Early Stopping greift. Siehe Early Stopping in Gradient Boosting für eine detailliertere Diskussion der Interaktion zwischen learning_rate und n_estimators. Siehe [R2007].

1.11.1.2.6. Subsampling#

[Friedman2002] schlug stochastisches Gradient Boosting vor, das Gradient Boosting mit Bootstrap-Mittelung (Bagging) kombiniert. Bei jeder Iteration wird der Basis-Klassifikator auf einem Bruchteil subsample der verfügbaren Trainingsdaten trainiert. Die Stichprobe wird ohne Zurücklegen gezogen. Ein typischer Wert für subsample ist 0.5.

Die Abbildung unten veranschaulicht die Auswirkung von Schrumpfung und Subsampling auf die Güte der Anpassung des Modells. Wir können deutlich sehen, dass Schrumpfung ohne Schrumpfung überlegen ist. Subsampling mit Schrumpfung kann die Genauigkeit des Modells weiter erhöhen. Subsampling ohne Schrumpfung schneidet dagegen schlecht ab.

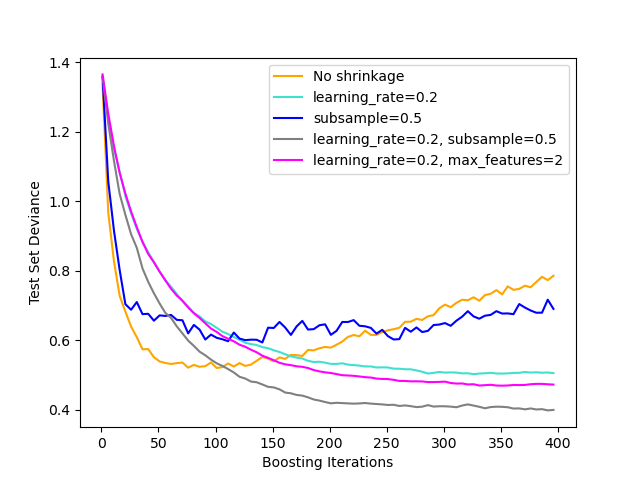
../_images/sphx_glr_plot_gradient_boosting_regularization_001.png

Eine weitere Strategie zur Reduzierung der Varianz ist das Subsampling von Merkmalen, analog zu den zufälligen Teilungen in RandomForestClassifier. Die Anzahl der gesampelten Merkmale kann über den Parameter max_features gesteuert werden.

Hinweis

Die Verwendung eines kleinen max_features-Werts kann die Laufzeit erheblich verkürzen.

Stochastisches Gradient Boosting ermöglicht die Berechnung von Out-of-Bag-Schätzungen des Test-Deviance, indem die Verbesserung der Deviance bei den Beispielen berechnet wird, die nicht in der Bootstrap-Stichprobe enthalten sind (d. h. die Out-of-Bag-Beispiele). Die Verbesserungen werden im Attribut oob_improvement_ gespeichert. oob_improvement_[i] enthält die Verbesserung in Bezug auf den Verlust bei den OOB-Stichproben, wenn Sie die i-te Stufe zu den aktuellen Vorhersagen hinzufügen. Out-of-Bag-Schätzungen können zur Modellauswahl verwendet werden, z. B. um die optimale Anzahl von Iterationen zu bestimmen. OOB-Schätzungen sind in der Regel sehr pessimistisch, daher empfehlen wir, stattdessen Kreuzvalidierung zu verwenden und OOB nur dann zu verwenden, wenn Kreuzvalidierung zu zeitaufwändig ist.

Beispiele

1.11.1.2.7. Interpretation mit Merkmalswichtigkeit#

Einzelne Entscheidungsbäume können leicht interpretiert werden, indem einfach die Baumstruktur visualisiert wird. Gradient-Boosting-Modelle bestehen jedoch aus Hunderten von Regressionsbäumen, daher können sie nicht leicht durch visuelle Inspektion der einzelnen Bäume interpretiert werden. Glücklicherweise wurden eine Reihe von Techniken vorgeschlagen, um Gradient-Boosting-Modelle zusammenzufassen und zu interpretieren.

Oft tragen Merkmale nicht gleichmäßig zur Vorhersage der Zielvariable bei; in vielen Situationen sind die meisten Merkmale tatsächlich irrelevant. Bei der Interpretation eines Modells ist die erste Frage in der Regel: Was sind diese wichtigen Merkmale und wie tragen sie zur Vorhersage der Zielvariable bei?

Einzelne Entscheidungsbäume führen intrinsisch eine Merkmalsauswahl durch, indem sie geeignete Teilungspunkte auswählen. Diese Information kann verwendet werden, um die Wichtigkeit jedes Merkmals zu messen; die Grundidee ist: Je öfter ein Merkmal in den Teilungspunkten eines Baumes verwendet wird, desto wichtiger ist dieses Merkmal. Diese Vorstellung von Wichtigkeit kann auf Entscheidungsbaum-Ensembles erweitert werden, indem einfach die Unreinheit-basierte Merkmalswichtigkeit jedes Baumes gemittelt wird (siehe Bewertung der Merkmalswichtigkeit für weitere Details).

Die Merkmalswichtigkeitswerte eines angepassten Gradient-Boosting-Modells können über die Eigenschaft feature_importances_ abgerufen werden.

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_
array([0.107, 0.105, 0.113, 0.0987, 0.0947,
       0.107, 0.0916, 0.0972, 0.0958, 0.0906])

Beachten Sie, dass diese Berechnung der Merkmalswichtigkeit auf der Entropie basiert und sich von sklearn.inspection.permutation_importance unterscheidet, das auf der Permutation der Merkmale basiert.

Beispiele

Gradient Boosting Regression

Referenzen

[Friedman2001] (1,2,3,4)

Friedman, J.H. (2001). Greedy function approximation: A gradient boosting machine. Annals of Statistics, 29, 1189-1232.

[Friedman2002]

Friedman, J.H. (2002). Stochastic gradient boosting.. Computational Statistics & Data Analysis, 38, 367-378.

[R2007]

G. Ridgeway (2006). Generalized Boosted Models: A guide to the gbm package

1.11.2. Random Forests und andere randomisierte Baum-Ensembles#

Das Modul sklearn.ensemble enthält zwei Mittelwertbildungsalgorithmen, die auf randomisierten Entscheidungsbäumen basieren: den RandomForest-Algorithmus und die Extra-Trees-Methode. Beide Algorithmen sind Perturb-and-Combine-Techniken [B1998], die speziell für Bäume entwickelt wurden. Das bedeutet, dass ein vielfältiger Satz von Klassifikatoren durch die Einführung von Zufälligkeit in die Konstruktion des Klassifikators erstellt wird. Die Vorhersage des Ensembles ist die gemittelte Vorhersage der einzelnen Klassifikatoren.

Wie andere Klassifikatoren müssen Forest-Klassifikatoren mit zwei Arrays angepasst werden: ein spärliches oder dichtes Array X der Form (n_samples, n_features), das die Trainingsstichproben enthält, und ein Array Y der Form (n_samples,), das die Zielwerte (Klassenbezeichnungen) für die Trainingsstichproben enthält.

>>> from sklearn.ensemble import RandomForestClassifier
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, Y)

Wie Entscheidungsbäume erweitern auch Baum-Wälder auf Probleme mit mehreren Ausgaben (wenn Y ein Array der Form (n_samples, n_outputs) ist).

1.11.2.1. Random Forests#

Bei Random Forests (siehe Klassen RandomForestClassifier und RandomForestRegressor) wird jeder Baum im Ensemble aus einer Stichprobe gezogen, die mit Zurücklegen (d. h. einer Bootstrap-Stichprobe) aus dem Trainingsdatensatz gezogen wird.

Während der Konstruktion jedes Baumes im Wald wird eine zufällige Teilmenge der Merkmale betrachtet. Die Größe dieser Teilmenge wird durch den Parameter max_features gesteuert; sie kann entweder alle Eingabemerkmale oder eine zufällige Teilmenge davon enthalten (siehe die Richtlinien zur Parameterabstimmung für weitere Details).

Der Zweck dieser beiden Zufälligkeitsquellen (Bootstrapping der Stichproben und zufällige Auswahl von Merkmalen bei jeder Teilung) ist die Reduzierung der Varianz des Forest-Schätzers. Tatsächlich weisen einzelne Entscheidungsbäume typischerweise eine hohe Varianz auf und neigen zum Überanpassen. Die eingeführte Zufälligkeit in Wäldern ergibt Entscheidungsbäume mit einigermaßen entkoppelten Vorhersagefehlern. Durch Mittelung dieser Vorhersagen können einige Fehler ausgemittelt werden. Random Forests erzielen eine reduzierte Varianz durch die Kombination verschiedener Bäume, manchmal auf Kosten einer leichten Zunahme des Bias. In der Praxis ist die Varianzreduzierung oft signifikant, was zu einem insgesamt besseren Modell führt.

Beim Aufbau jedes Baumes im Wald wird die "beste" Teilung (d. h. äquivalent zur Übergabe von splitter="best" an die zugrundeliegenden Entscheidungsbäume) gemäß dem Unreinheitskriterium gewählt. Siehe die CART mathematische Formulierung für weitere Details.

Im Gegensatz zur ursprünglichen Veröffentlichung [B2001] kombiniert die scikit-learn-Implementierung Klassifikatoren, indem sie ihre Wahrscheinlichkeitsvorhersagen mittelt, anstatt jeden Klassifikator für eine einzelne Klasse abstimmen zu lassen.

Eine wettbewerbsfähige Alternative zu Random Forests sind Histogram-basierte Gradient-Boosting-Modelle (HGBT).

Aufbau von Bäumen: Random Forests stützen sich typischerweise auf tiefe Bäume (die einzeln überanpassen), was viel Rechenressourcen beansprucht, da sie mehrere Teilungen und Auswertungen von Kandidaten-Teilungen erfordern. Boosting-Modelle bauen flache Bäume (die einzeln unteranpassen), die schneller anzupassen und vorherzusagen sind.
Sequentielles Boosting: Bei HGBT werden die Entscheidungsbäume sequenziell aufgebaut, wobei jeder Baum trainiert wird, um die Fehler des vorherigen Baumes zu korrigieren. Dies ermöglicht es ihnen, die Leistung des Modells mit relativ wenigen Bäumen iterativ zu verbessern. Im Gegensatz dazu verwenden Random Forests eine Mehrheitsabstimmung zur Vorhersage des Ergebnisses, was eine größere Anzahl von Bäumen erfordern kann, um das gleiche Genauigkeitsniveau zu erreichen.
Effiziente Binning: HGBT verwendet einen effizienten Binning-Algorithmus, der große Datensätze mit einer hohen Anzahl von Merkmalen verarbeiten kann. Der Binning-Algorithmus kann die Daten vorverarbeiten, um die anschließende Baumkonstruktion zu beschleunigen (siehe Warum es schneller ist). Im Gegensatz dazu verwendet die scikit-learn-Implementierung von Random Forests kein Binning und stützt sich auf exakte Teilungen, was rechenintensiv sein kann.

Insgesamt hängen die Rechenkosten von HGBT im Vergleich zu RF von den spezifischen Merkmalen des Datensatzes und der Modellierungsaufgabe ab. Es ist ratsam, beide Modelle auszuprobieren und ihre Leistung und Recheneffizienz für Ihr spezifisches Problem zu vergleichen, um zu entscheiden, welches Modell am besten geeignet ist.

Beispiele

Vergleich von Random Forests und Histogram Gradient Boosting Modellen

1.11.2.2. Extrem zufällige Bäume#

Bei extrem zufälligen Bäumen (siehe Klassen ExtraTreesClassifier und ExtraTreesRegressor) geht die Zufälligkeit einen Schritt weiter in der Art und Weise, wie Teilungen berechnet werden. Wie bei Random Forests wird eine zufällige Teilmenge von Kandidatenmerkmalen verwendet, aber anstatt nach den diskriminativsten Schwellenwerten zu suchen, werden für jedes Kandidatenmerkmal zufällig Schwellenwerte gezogen und der beste dieser zufällig erzeugten Schwellenwerte wird als Teilungsregel gewählt. Dies ermöglicht es in der Regel, die Varianz des Modells etwas stärker zu reduzieren, auf Kosten einer etwas größeren Zunahme des Bias.

>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import make_blobs
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.tree import DecisionTreeClassifier

>>> X, y = make_blobs(n_samples=10000, n_features=10, centers=100,
...     random_state=0)

>>> clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2,
...     random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
np.float64(0.98)

>>> clf = RandomForestClassifier(n_estimators=10, max_depth=None,
...     min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
np.float64(0.999)

>>> clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,
...     min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean() > 0.999
np.True_

../_images/sphx_glr_plot_forest_iris_001.png

1.11.2.3. Parameter#

Die wichtigsten Parameter, die bei der Verwendung dieser Methoden angepasst werden müssen, sind n_estimators und max_features. Ersteres ist die Anzahl der Bäume im Wald. Je größer, desto besser, aber auch desto länger dauert die Berechnung. Beachten Sie außerdem, dass sich die Ergebnisse über eine kritische Anzahl von Bäumen hinaus nicht mehr wesentlich verbessern. Letzteres ist die Größe der zufälligen Teilmengen von Merkmalen, die bei der Aufteilung eines Knotens berücksichtigt werden. Je niedriger der Wert, desto größer ist die Reduzierung der Varianz, aber desto größer ist auch die Erhöhung des Bias. Empirisch gute Standardwerte sind max_features=1.0 oder äquivalent max_features=None (immer alle Merkmale anstelle einer zufälligen Teilmenge berücksichtigen) für Regressionsprobleme und max_features="sqrt" (Verwendung einer zufälligen Teilmenge der Größe sqrt(n_features)) für Klassifizierungsaufgaben (wobei n_features die Anzahl der Merkmale in den Daten ist). Der Standardwert von max_features=1.0 ist äquivalent zu Bagged Trees, und mehr Zufälligkeit kann durch kleinere Werte erreicht werden (z. B. ist 0.3 ein typischer Standardwert in der Literatur). Gute Ergebnisse werden oft erzielt, wenn max_depth=None in Kombination mit min_samples_split=2 eingestellt wird (d. h. wenn die Bäume vollständig entwickelt werden). Beachten Sie jedoch, dass diese Werte normalerweise nicht optimal sind und zu Modellen führen können, die viel RAM verbrauchen. Die besten Parameterwerte sollten immer mittels Kreuzvalidierung ermittelt werden. Beachten Sie außerdem, dass bei Random Forests standardmäßig Bootstrap-Stichproben verwendet werden (bootstrap=True), während die Standardstrategie für Extra-Trees die Verwendung des gesamten Datensatzes ist (bootstrap=False). Bei Verwendung von Bootstrap-Stichproben kann der Generalisierungsfehler anhand der ausgelassenen oder Out-of-Bag-Stichproben geschätzt werden. Dies kann durch Setzen von oob_score=True aktiviert werden.

Hinweis

Die Größe des Modells mit den Standardparametern ist \(O( M * N * log (N) )\), wobei \(M\) die Anzahl der Bäume und \(N\) die Anzahl der Stichproben ist. Um die Größe des Modells zu reduzieren, können Sie diese Parameter ändern: min_samples_split, max_leaf_nodes, max_depth und min_samples_leaf.

1.11.2.4. Parallelisierung#

Schließlich bietet dieses Modul auch die parallele Konstruktion der Bäume und die parallele Berechnung der Vorhersagen über den Parameter n_jobs. Wenn n_jobs=k ist, werden die Berechnungen in k Jobs aufgeteilt und auf k Kerne der Maschine ausgeführt. Wenn n_jobs=-1 ist, werden alle verfügbaren Kerne der Maschine genutzt. Beachten Sie, dass die Beschleunigung aufgrund des Kommunikationsaufwands zwischen Prozessen möglicherweise nicht linear ist (d. h. die Verwendung von k Jobs wird leider nicht k Mal so schnell sein). Eine signifikante Beschleunigung kann jedoch beim Aufbau einer großen Anzahl von Bäumen oder beim Aufbau eines einzelnen Baumes, der eine gewisse Zeit in Anspruch nimmt (z. B. bei großen Datensätzen), erzielt werden.

Beispiele

Referenzen

[B2001]

Breiman, “Random Forests”, Machine Learning, 45(1), 5-32, 2001.

[B1998]

Breiman, “Arcing Classifiers”, Annals of Statistics 1998.

P. Geurts, D. Ernst. und L. Wehenkel, „Extremely randomized trees“, Machine Learning, 63(1), 3-42, 2006.

1.11.2.5. Bewertung der Merkmalbedeutung#

Der relative Rang (d. h. die Tiefe) eines Merkmals, das als Entscheidungsknoten in einem Baum verwendet wird, kann zur Bewertung der relativen Bedeutung dieses Merkmals für die Vorhersagbarkeit der Zielvariablen verwendet werden. Merkmale, die am oberen Ende des Baumes verwendet werden, tragen zu einem größeren Bruchteil der Eingabestichproben zur endgültigen Vorhersageentscheidung bei. Der erwartete Bruchteil der Stichproben, zu dem sie beitragen, kann somit als Schätzung der relativen Bedeutung der Merkmale verwendet werden. In scikit-learn wird der Stichprobenanteil, zu dem ein Merkmal beiträgt, mit der Verringerung der durch das Aufteilen entstehenden Unreinheit kombiniert, um eine normalisierte Schätzung der prädiktiven Kraft dieses Merkmals zu erstellen.

Durch das Mittelwertbilden der Schätzungen der prädiktiven Fähigkeit über mehrere zufällige Bäume kann die Varianz einer solchen Schätzung reduziert und für die Merkmalsauswahl verwendet werden. Dies ist als mittlere Verringerung der Unreinheit oder MDI bekannt. Weitere Informationen zu MDI und der Bewertung der Merkmalbedeutung mit Random Forests finden Sie unter [L2014].

Warnung

Die auf Unreinheit basierenden Merkmalbedeutungen, die bei baumbasierten Modellen berechnet werden, leiden unter zwei Mängeln, die zu irreführenden Schlussfolgerungen führen können. Erstens werden sie auf Statistiken berechnet, die aus dem Trainingsdatensatz abgeleitet sind, und informieren uns daher nicht notwendigerweise darüber, welche Merkmale für gute Vorhersagen auf einem zurückgehaltenen Datensatz am wichtigsten sind. Zweitens bevorzugen sie Merkmale mit hoher Kardinalität, d. h. Merkmale mit vielen eindeutigen Werten. Permutations-Merkmalbedeutung ist eine Alternative zur auf Unreinheit basierenden Merkmalbedeutung, die diese Mängel nicht aufweist. Diese beiden Methoden zur Ermittlung der Merkmalbedeutung werden untersucht in: Permutations-Merkmalbedeutung im Vergleich zur Random Forest Merkmalbedeutung (MDI).

In der Praxis werden diese Schätzungen als Attribut mit dem Namen feature_importances_ auf dem angepassten Modell gespeichert. Dies ist ein Array der Form (n_features,), dessen Werte positiv sind und sich zu 1.0 aufsummieren. Je höher der Wert, desto wichtiger ist der Beitrag des entsprechenden Merkmals zur Vorhersagefunktion.

Beispiele

Merkmalswichtigkeiten mit einem Wald von Bäumen

Referenzen

[L2014]

G. Louppe, „Understanding Random Forests: From Theory to Practice“, PhD-Arbeit, U. von Lüttich, 2014.

1.11.2.6. Totally Random Trees Embedding#

RandomTreesEmbedding implementiert eine unbeaufsichtigte Transformation der Daten. Mithilfe eines Waldes von vollständig zufälligen Bäumen kodiert RandomTreesEmbedding die Daten anhand der Indizes der Blätter, in denen ein Datenpunkt endet. Dieser Index wird dann auf eine One-of-K-Weise kodiert, was zu einer hochdimensionalen, spärlichen binären Kodierung führt. Diese Kodierung kann sehr effizient berechnet werden und dann als Grundlage für andere Lernaufgaben dienen. Die Größe und Spärlichkeit des Codes kann durch die Wahl der Anzahl der Bäume und der maximalen Tiefe pro Baum beeinflusst werden. Für jeden Baum im Ensemble enthält die Kodierung einen Eintrag von Eins. Die Größe der Kodierung beträgt höchstens n_estimators * 2 ** max_depth, die maximale Anzahl von Blättern im Wald.

Da benachbarte Datenpunkte mit höherer Wahrscheinlichkeit im selben Blatt eines Baumes liegen, führt die Transformation eine implizite, nicht-parametrische Dichteschätzung durch.

Beispiele

Hashing-Merkmals-Transformation mit Totally Random Trees
Manifold Learning auf handgeschriebenen Ziffern: Locally Linear Embedding, Isomap… vergleicht nicht-lineare Dimensionalitätsreduktionstechniken auf handgeschriebenen Ziffern.
Merkmals-Transformationen mit Ensemble von Bäumen vergleicht beaufsichtigte und unbeaufsichtigte baumbasierte Merkmals-Transformationen.

Siehe auch

Manifold Learning-Techniken können ebenfalls nützlich sein, um nicht-lineare Darstellungen des Merkmalsraums abzuleiten. Auch diese Ansätze konzentrieren sich auf die Dimensionalitätsreduktion.

1.11.2.7. Anpassen zusätzlicher Bäume#

RandomForest, Extra-Trees und RandomTreesEmbedding-Estimator unterstützen warm_start=True, was es Ihnen ermöglicht, einem bereits angepassten Modell weitere Bäume hinzuzufügen.

>>> from sklearn.datasets import make_classification
>>> from sklearn.ensemble import RandomForestClassifier

>>> X, y = make_classification(n_samples=100, random_state=1)
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, y)  # fit with 10 trees
>>> len(clf.estimators_)
10
>>> # set warm_start and increase num of estimators
>>> _ = clf.set_params(n_estimators=20, warm_start=True)
>>> _ = clf.fit(X, y) # fit additional 10 trees
>>> len(clf.estimators_)
20

Wenn random_state ebenfalls gesetzt ist, bleibt der interne Zufallszustand auch zwischen fit-Aufrufen erhalten. Das bedeutet, dass das einmalige Trainieren eines Modells mit n Schätzern dasselbe ist wie der iterative Aufbau des Modells durch mehrere fit-Aufrufe, wobei die endgültige Anzahl der Schätzer gleich n ist.

>>> clf = RandomForestClassifier(n_estimators=20)  # set `n_estimators` to 10 + 10
>>> _ = clf.fit(X, y)  # fit `estimators_` will be the same as `clf` above

Beachten Sie, dass dies vom üblichen Verhalten von random_state abweicht, da es *nicht* zu denselben Ergebnissen bei verschiedenen Aufrufen führt.

1.11.3. Bagging-Meta-Estimator#

In Ensemble-Algorithmen bilden Bagging-Methoden eine Klasse von Algorithmen, die mehrere Instanzen eines Black-Box-Schätzers auf zufälligen Teilmengen des ursprünglichen Trainingssatzes erstellen und dann ihre individuellen Vorhersagen aggregieren, um eine endgültige Vorhersage zu bilden. Diese Methoden werden verwendet, um die Varianz eines Basis-Schätzers (z. B. eines Entscheidungsbaums) zu reduzieren, indem Zufälligkeit in seinen Konstruktionsprozess eingeführt und dann ein Ensemble daraus gebildet wird. In vielen Fällen stellen Bagging-Methoden eine sehr einfache Möglichkeit dar, eine Verbesserung gegenüber einem einzelnen Modell zu erzielen, ohne dass der zugrunde liegende Basisalgorithmus angepasst werden muss. Da sie eine Möglichkeit zur Reduzierung von Overfitting bieten, funktionieren Bagging-Methoden am besten mit starken und komplexen Modellen (z. B. vollständig entwickelten Entscheidungsbäumen), im Gegensatz zu Boosting-Methoden, die normalerweise am besten mit schwachen Modellen (z. B. flachen Entscheidungsbäumen) funktionieren.

Bagging-Methoden gibt es in vielen Varianten, sie unterscheiden sich jedoch hauptsächlich durch die Art und Weise, wie sie zufällige Teilmengen des Trainingsdatensatzes ziehen.

Wenn zufällige Teilmengen des Datensatzes als zufällige Teilmengen der Stichproben gezogen werden, ist dieser Algorithmus als Pasting [B1999] bekannt.
Wenn Stichproben mit Zurücklegen gezogen werden, ist die Methode als Bagging [B1996] bekannt.
Wenn zufällige Teilmengen des Datensatzes als zufällige Teilmengen der Merkmale gezogen werden, ist die Methode als Random Subspaces [H1998] bekannt.
Schließlich, wenn Basis-Schätzer auf Teilmengen von sowohl Stichproben als auch Merkmalen erstellt werden, ist die Methode als Random Patches [LG2012] bekannt.

In scikit-learn werden Bagging-Methoden als einheitlicher BaggingClassifier-Meta-Estimator (bzw. BaggingRegressor) angeboten, der als Eingabe einen vom Benutzer spezifizierten Estimator zusammen mit Parametern zur Angabe der Strategie zum Ziehen zufälliger Teilmengen entgegennimmt. Insbesondere steuern max_samples und max_features die Größe der Teilmengen (hinsichtlich Stichproben und Merkmalen), während bootstrap und bootstrap_features steuern, ob Stichproben und Merkmale mit oder ohne Zurücklegen gezogen werden. Bei Verwendung einer Teilmenge der verfügbaren Stichproben kann die Generalisierungsgenauigkeit mit den Out-of-Bag-Stichproben geschätzt werden, indem oob_score=True gesetzt wird. Als Beispiel zeigt der folgende Ausschnitt, wie ein Bagging-Ensemble von KNeighborsClassifier-Estimator instanziiert wird, die jeweils auf zufälligen Teilmengen von 50 % der Stichproben und 50 % der Merkmale aufgebaut sind.

>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
...                             max_samples=0.5, max_features=0.5)

Beispiele

Einzelner Estimator versus Bagging: Bias-Varianz-Zerlegung

Referenzen

[B1999]

L. Breiman, “Pasting small votes for classification in large databases and on-line”, Machine Learning, 36(1), 85-103, 1999.

[B1996]

L. Breiman, “Bagging predictors”, Machine Learning, 24(2), 123-140, 1996.

[H1998]

T. Ho, “The random subspace method for constructing decision forests”, Pattern Analysis and Machine Intelligence, 20(8), 832-844, 1998.

[LG2012]

G. Louppe und P. Geurts, “Ensembles on Random Patches”, Machine Learning and Knowledge Discovery in Databases, 346-361, 2012.

1.11.4. Voting Classifier#

Die Idee hinter dem VotingClassifier ist es, konzeptionell unterschiedliche Maschinenlern-Klassifikatoren zu kombinieren und eine Mehrheitsentscheidung oder die durchschnittlichen vorhergesagten Wahrscheinlichkeiten (Soft Vote) zu verwenden, um die Klassenlabels vorherzusagen. Ein solcher Klassifikator kann für eine Reihe von gleichermaßen gut funktionierenden Modellen nützlich sein, um deren individuelle Schwächen auszugleichen.

1.11.4.1. Mehrheitsklassen-Labels (Majority/Hard Voting)#

Beim Mehrheits-Voting ist das vorhergesagte Klassenlabel für eine bestimmte Stichprobe das Klassenlabel, das die Mehrheit (Modus) der von jedem einzelnen Klassifikator vorhergesagten Klassenlabels darstellt.

Z. B. wenn die Vorhersage für eine gegebene Stichprobe

Klassifikator 1 -> Klasse 1
Klassifikator 2 -> Klasse 1
Klassifikator 3 -> Klasse 2

ist, klassifiziert der VotingClassifier (mit voting='hard') die Stichprobe als "Klasse 1" basierend auf dem Mehrheitsklassenlabel.

Bei Gleichstand wählt der VotingClassifier die Klasse basierend auf der aufsteigenden Sortierreihenfolge aus. Z. B. im folgenden Szenario

Klassifikator 1 -> Klasse 2
Klassifikator 2 -> Klasse 1

wird das Klassenlabel 1 der Stichprobe zugewiesen.

1.11.4.2. Verwendung#

Das folgende Beispiel zeigt, wie der Mehrheitsregel-Klassifikator angepasst wird

>>> from sklearn import datasets
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import VotingClassifier

>>> iris = datasets.load_iris()
>>> X, y = iris.data[:, 1:3], iris.target

>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(n_estimators=50, random_state=1)
>>> clf3 = GaussianNB()

>>> eclf = VotingClassifier(
...     estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
...     voting='hard')

>>> for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
...     scores = cross_val_score(clf, X, y, scoring='accuracy', cv=5)
...     print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
Accuracy: 0.95 (+/- 0.04) [Logistic Regression]
Accuracy: 0.94 (+/- 0.04) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [naive Bayes]
Accuracy: 0.95 (+/- 0.04) [Ensemble]

1.11.4.3. Gewichteter Durchschnitt der Wahrscheinlichkeiten (Soft Voting)#

Im Gegensatz zum Mehrheits-Voting (Hard Voting) gibt Soft Voting das Klassenlabel als Argmax der Summe der vorhergesagten Wahrscheinlichkeiten zurück.

Spezifische Gewichte können jedem Klassifikator über den Parameter weights zugewiesen werden. Wenn Gewichte angegeben werden, werden die vorhergesagten Klassenwahrscheinlichkeiten für jeden Klassifikator gesammelt, mit dem Klassifikatorgewicht multipliziert und gemittelt. Das endgültige Klassenlabel wird dann vom Klassenlabel mit der höchsten durchschnittlichen Wahrscheinlichkeit abgeleitet.

Um dies anhand eines einfachen Beispiels zu veranschaulichen, nehmen wir an, wir haben 3 Klassifikatoren und ein 3-Klassen-Klassifikationsproblem, bei dem wir allen Klassifikatoren gleiche Gewichte zuweisen: w1=1, w2=1, w3=1.

Die gewichteten Durchschnittswahrscheinlichkeiten für eine Stichprobe würden dann wie folgt berechnet:

Klassifikator	Klasse 1	Klasse 2	Klasse 3
Klassifikator 1	w1 * 0.2	w1 * 0.5	w1 * 0.3
Klassifikator 2	w2 * 0.6	w2 * 0.3	w2 * 0.1
Klassifikator 3	w3 * 0.3	w3 * 0.4	w3 * 0.3
gewichteter Durchschnitt	0.37	0.4	0.23

Hier ist das vorhergesagte Klassenlabel 2, da es die höchste durchschnittliche vorhergesagte Wahrscheinlichkeit hat. Siehe das Beispiel unter Visualisierung der probabilistischen Vorhersagen eines VotingClassifier für eine Demonstration, wie das vorhergesagte Klassenlabel aus dem gewichteten Durchschnitt der vorhergesagten Wahrscheinlichkeiten abgeleitet werden kann.

Die folgende Abbildung veranschaulicht, wie sich die Entscheidungsregionen ändern können, wenn ein Soft VotingClassifier mit Gewichten auf drei lineare Modelle trainiert wird.

../_images/sphx_glr_plot_voting_decision_regions_002.png

1.11.4.4. Verwendung#

Um die Klassenlabels basierend auf den vorhergesagten Klassenwahrscheinlichkeiten vorherzusagen (scikit-learn-Estimator im VotingClassifier müssen die Methode predict_proba unterstützen)

>>> eclf = VotingClassifier(
...     estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
...     voting='soft'
... )

Optional können Gewichte für die einzelnen Klassifikatoren angegeben werden

>>> eclf = VotingClassifier(
...     estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
...     voting='soft', weights=[2,5,1]
... )

1.11.5. Voting Regressor#

Die Idee hinter dem VotingRegressor ist es, konzeptionell unterschiedliche Maschinenlern-Regressoren zu kombinieren und die durchschnittlichen vorhergesagten Werte zurückzugeben. Ein solcher Regressor kann für eine Reihe von gleichermaßen gut funktionierenden Modellen nützlich sein, um deren individuelle Schwächen auszugleichen.

1.11.5.1. Verwendung#

Das folgende Beispiel zeigt, wie der VotingRegressor angepasst wird

>>> from sklearn.datasets import load_diabetes
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import RandomForestRegressor
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.ensemble import VotingRegressor

>>> # Loading some example data
>>> X, y = load_diabetes(return_X_y=True)

>>> # Training classifiers
>>> reg1 = GradientBoostingRegressor(random_state=1)
>>> reg2 = RandomForestRegressor(random_state=1)
>>> reg3 = LinearRegression()
>>> ereg = VotingRegressor(estimators=[('gb', reg1), ('rf', reg2), ('lr', reg3)])
>>> ereg = ereg.fit(X, y)

../_images/sphx_glr_plot_voting_regressor_001.png

Beispiele

Vorhersagen von einzelnen und abstimmenden Regressionsmodellen plotten

1.11.6. Stacked Generalization#

Stacked Generalization ist eine Methode zur Kombination von Estimatorn, um deren Bias zu reduzieren [W1992] [HTF]. Genauer gesagt werden die Vorhersagen jedes einzelnen Estimators gestapelt und als Eingabe für einen endgültigen Estimator verwendet, um die Vorhersage zu berechnen. Dieser endgültige Estimator wird durch Kreuzvalidierung trainiert.

Der StackingClassifier und StackingRegressor bieten solche Strategien, die auf Klassifikations- und Regressionsprobleme angewendet werden können.

Der Parameter estimators entspricht der Liste der Estimatorn, die parallel auf die Eingabedaten gestapelt werden. Er sollte als Liste von Namen und Estimatorn angegeben werden.

>>> from sklearn.linear_model import RidgeCV, LassoCV
>>> from sklearn.neighbors import KNeighborsRegressor
>>> estimators = [('ridge', RidgeCV()),
...               ('lasso', LassoCV(random_state=42)),
...               ('knr', KNeighborsRegressor(n_neighbors=20,
...                                           metric='euclidean'))]

Der final_estimator verwendet die Vorhersagen der estimators als Eingabe. Er muss ein Klassifikator oder ein Regressor sein, wenn StackingClassifier oder StackingRegressor verwendet wird, bzw.

>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import StackingRegressor
>>> final_estimator = GradientBoostingRegressor(
...     n_estimators=25, subsample=0.5, min_samples_leaf=25, max_features=1,
...     random_state=42)
>>> reg = StackingRegressor(
...     estimators=estimators,
...     final_estimator=final_estimator)

Zum Trainieren der estimators und des final_estimator muss die Methode fit auf den Trainingsdaten aufgerufen werden.

>>> from sklearn.datasets import load_diabetes
>>> X, y = load_diabetes(return_X_y=True)
>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
...                                                     random_state=42)
>>> reg.fit(X_train, y_train)
StackingRegressor(...)

Während des Trainings werden die estimators auf den gesamten Trainingsdaten X_train angepasst. Sie werden beim Aufruf von predict oder predict_proba verwendet. Um zu generalisieren und Overfitting zu vermeiden, wird der final_estimator intern mithilfe von sklearn.model_selection.cross_val_predict auf Out-Samples trainiert.

Bei StackingClassifier wird die Ausgabe der estimators durch den Parameter stack_method gesteuert und von jedem Estimator aufgerufen. Dieser Parameter ist entweder ein String, der die Namen der Estimator-Methoden angibt, oder 'auto', was automatisch eine verfügbare Methode identifiziert, je nach Verfügbarkeit, getestet in der Reihenfolge der Präferenz: predict_proba, decision_function und predict.

Ein StackingRegressor und StackingClassifier können wie jeder andere Regressor oder Klassifikator verwendet werden und stellen eine predict, predict_proba oder decision_function Methode bereit, z. B.

>>> y_pred = reg.predict(X_test)
>>> from sklearn.metrics import r2_score
>>> print('R2 score: {:.2f}'.format(r2_score(y_test, y_pred)))
R2 score: 0.53

Beachten Sie, dass es auch möglich ist, die Ausgabe der gestapelten estimators über die Methode transform zu erhalten.

>>> reg.transform(X_test[:5])
array([[142, 138, 146],
       [179, 182, 151],
       [139, 132, 158],
       [286, 292, 225],
       [126, 124, 164]])

In der Praxis erzielt ein Stacking-Prädiktor eine Vorhersagequalität, die der des besten Prädiktors der Basisschicht entspricht, und übertrifft diese manchmal sogar, indem die verschiedenen Stärken dieser Prädiktoren kombiniert werden. Das Training eines Stacking-Prädiktors ist jedoch rechenintensiv.

Hinweis

Bei StackingClassifier wird die erste Spalte bei binären Klassifikationsproblemen fallen gelassen, wenn stack_method_='predict_proba' verwendet wird. Tatsächlich sind beide Wahrscheinlichkeitsspalten, die von jedem Estimator vorhergesagt werden, perfekt kollinear.

Hinweis

Mehrere Stacking-Schichten können durch Zuweisung von final_estimator zu einem StackingClassifier oder StackingRegressor erreicht werden.

>>> final_layer_rfr = RandomForestRegressor(
...     n_estimators=10, max_features=1, max_leaf_nodes=5,random_state=42)
>>> final_layer_gbr = GradientBoostingRegressor(
...     n_estimators=10, max_features=1, max_leaf_nodes=5,random_state=42)
>>> final_layer = StackingRegressor(
...     estimators=[('rf', final_layer_rfr),
...                 ('gbrt', final_layer_gbr)],
...     final_estimator=RidgeCV()
...     )
>>> multi_layer_regressor = StackingRegressor(
...     estimators=[('ridge', RidgeCV()),
...                 ('lasso', LassoCV(random_state=42)),
...                 ('knr', KNeighborsRegressor(n_neighbors=20,
...                                             metric='euclidean'))],
...     final_estimator=final_layer
... )
>>> multi_layer_regressor.fit(X_train, y_train)
StackingRegressor(...)
>>> print('R2 score: {:.2f}'
...       .format(multi_layer_regressor.score(X_test, y_test)))
R2 score: 0.53

Beispiele

Prädiktoren mit Stacking kombinieren

Referenzen

[W1992]

Wolpert, David H. “Stacked generalization.” Neural networks 5.2 (1992): 241-259.

1.11.7. AdaBoost#

Das Modul sklearn.ensemble enthält den beliebten Boosting-Algorithmus AdaBoost, der 1995 von Freund und Schapire eingeführt wurde [FS1995].

Das Kernprinzip von AdaBoost besteht darin, eine Sequenz von schwachen Lernenden (d. h. Modelle, die nur geringfügig besser sind als zufälliges Raten, wie z. B. kleine Entscheidungsbäume) auf wiederholt modifizierten Versionen der Daten anzupassen. Die Vorhersagen aller werden dann durch eine gewichtete Mehrheitsentscheidung (oder Summe) kombiniert, um die endgültige Vorhersage zu erzeugen. Die Datenmodifikationen bei jeder sogenannten Boosting-Iteration bestehen darin, Gewichte \(w_1\), \(w_2\), …, \(w_N\) auf jede der Trainingsstichproben anzuwenden. Anfangs werden diese Gewichte alle auf \(w_i = 1/N\) gesetzt, so dass der erste Schritt einfach einen schwachen Lernenden auf den Originaldaten trainiert. Bei jeder aufeinanderfolgenden Iteration werden die Stichprobengewichte individuell modifiziert und der Lernalgorithmus erneut auf die neu gewichteten Daten angewendet. In einer gegebenen Iteration werden die Trainingsbeispiele, die vom gesteigerten Modell, das in der vorherigen Iteration induziert wurde, falsch vorhergesagt wurden, mit erhöhten Gewichten versehen, während die Gewichte für diejenigen, die korrekt vorhergesagt wurden, verringert werden. Mit fortschreitenden Iterationen erhalten Beispiele, die schwer vorherzusagen sind, zunehmend Einfluss. Jeder nachfolgende schwache Lernende wird dadurch gezwungen, sich auf die Beispiele zu konzentrieren, die von den vorherigen in der Sequenz verfehlt wurden [HTF].

../_images/sphx_glr_plot_adaboost_multiclass_001.png

AdaBoost kann sowohl für Klassifikations- als auch für Regressionsprobleme verwendet werden.

Für multiklasse Klassifikation implementiert AdaBoostClassifier AdaBoost.SAMME [ZZRH2009].
Für Regression implementiert AdaBoostRegressor AdaBoost.R2 [D1997].

1.11.7.1. Verwendung#

Das folgende Beispiel zeigt, wie ein AdaBoost-Klassifikator mit 100 schwachen Lernenden angepasst wird.

>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import AdaBoostClassifier

>>> X, y = load_iris(return_X_y=True)
>>> clf = AdaBoostClassifier(n_estimators=100)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
np.float64(0.95)

Die Anzahl der schwachen Lernenden wird durch den Parameter n_estimators gesteuert. Der Parameter learning_rate steuert den Beitrag der schwachen Lernenden zur endgültigen Kombination. Standardmäßig sind schwache Lernende Decision Stumps. Unterschiedliche schwache Lernende können über den Parameter estimator spezifiziert werden. Die wichtigsten Parameter, die zur Erzielung guter Ergebnisse abgestimmt werden sollten, sind n_estimators und die Komplexität der Basis-Estimator (z. B. deren Tiefe max_depth oder die minimal erforderliche Anzahl von Stichproben, um eine Aufteilung zu berücksichtigen min_samples_split).

Beispiele

Multi-Klassen AdaBoosted Decision Trees zeigt die Leistung von AdaBoost bei einem Multi-Klassen-Problem.
Zwei-Klassen AdaBoost zeigt die Entscheidungsabgrenzung und die Werte der Entscheidungsfunktion für ein nicht-linear trennbares Zwei-Klassen-Problem mit AdaBoost-SAMME.
Entscheidungsbaum-Regression mit AdaBoost demonstriert Regression mit dem AdaBoost.R2-Algorithmus.

Referenzen

[FS1995]

Y. Freund und R. Schapire, „A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting“, 1997.

[ZZRH2009]

Zhu, H. Zou, S. Rosset, T. Hastie. „Multi-class AdaBoost“, 2009.

[D1997]

Drucker. „Improving Regressors using Boosting Techniques“, 1997.

[HTF] (1,2,3)

T. Hastie, R. Tibshirani und J. Friedman, „Elements of Statistical Learning Ed. 2“, Springer, 2009.

1.11. Ensembles: Gradienten-Boosting, Random Forests, Bagging, Voting, Stacking#

1.11.1. Gradienten-Boosted Trees#

1.11.1.1. Histogramm-basierte Gradienten-Boostung#

1.11.1.1.1. Verwendung#

1.11.1.1.2. Unterstützung für fehlende Werte#

1.11.1.1.3. Unterstützung für Sample-Gewichte#

1.11.1.1.4. Unterstützung für kategoriale Merkmale#

1.11.1.1.5. Monotone Einschränkungen#

1.11.1.1.6. Interaktionsbeschränkungen#

1.11.1.1.7. Low-Level-Parallelität#

1.11.1.1.8. Warum es schneller ist#

1.11.1.2. GradientBoostingClassifier und GradientBoostingRegressor#

1.11.1.2.1. Anpassen zusätzlicher schwacher Lerner#

1.11.1.2.2. Steuerung der Baumgröße#

1.11.1.2.3. Mathematische Formulierung#

1.11.1.2.4. Verlustfunktionen#

1.11.1.2.5. Schrumpfung durch Lernrate#

1.11.1.2.6. Subsampling#

1.11.1.2.7. Interpretation mit Merkmalswichtigkeit#

1.11.2. Random Forests und andere randomisierte Baum-Ensembles#

1.11.2.1. Random Forests#

1.11.2.2. Extrem zufällige Bäume#

1.11.2.3. Parameter#

1.11.2.4. Parallelisierung#

1.11.2.5. Bewertung der Merkmalbedeutung#

1.11.2.6. Totally Random Trees Embedding#

1.11.2.7. Anpassen zusätzlicher Bäume#

1.11.3. Bagging-Meta-Estimator#

1.11.4. Voting Classifier#

1.11.4.1. Mehrheitsklassen-Labels (Majority/Hard Voting)#

1.11.4.2. Verwendung#

1.11.4.3. Gewichteter Durchschnitt der Wahrscheinlichkeiten (Soft Voting)#

1.11.4.4. Verwendung#

1.11.5. Voting Regressor#

1.11.5.1. Verwendung#

1.11.6. Stacked Generalization#

1.11.7. AdaBoost#

1.11.7.1. Verwendung#

Diese Seite

1.11.1.2. `GradientBoostingClassifier` und `GradientBoostingRegressor`#