Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Visualisierung der probabilistischen Vorhersagen eines VotingClassifier#
Darstellung der vorhergesagten Klassenwahrscheinlichkeiten in einem Dummy-Datensatz, vorhergesagt von drei verschiedenen Klassifikatoren und gemittelt durch den VotingClassifier.
Zuerst werden drei lineare Klassifikatoren initialisiert. Zwei davon sind Spline-Modelle mit Interaktionstermen, eines verwendet konstante Extrapolation und das andere periodische Extrapolation. Der dritte Klassifikator ist ein Nystroem mit dem Standard-RBF-Kernel.
Im ersten Teil dieses Beispiels werden diese drei Klassifikatoren verwendet, um Soft-Voting mit VotingClassifier mit gewichteter Mittelung zu demonstrieren. Wir setzen weights=[2, 1, 3], was bedeutet, dass die Vorhersagen des Spline-Modells mit konstanter Extrapolation doppelt so stark gewichtet werden wie die des Spline-Modells mit periodischer Extrapolation, und die Vorhersagen des Nystroem-Modells dreimal so stark gewichtet werden wie die des Spline-Modells mit periodischer Extrapolation.
Der zweite Teil zeigt, wie Soft-Vorhersagen in Hard-Vorhersagen umgewandelt werden können.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Wir generieren zunächst einen verrauschten XOR-Datensatz, der eine binäre Klassifizierungsaufgabe darstellt.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from matplotlib.colors import ListedColormap
n_samples = 500
rng = np.random.default_rng(0)
feature_names = ["Feature #0", "Feature #1"]
common_scatter_plot_params = dict(
cmap=ListedColormap(["tab:red", "tab:blue"]),
edgecolor="white",
linewidth=1,
)
xor = pd.DataFrame(
np.random.RandomState(0).uniform(low=-1, high=1, size=(n_samples, 2)),
columns=feature_names,
)
noise = rng.normal(loc=0, scale=0.1, size=(n_samples, 2))
target_xor = np.logical_xor(
xor["Feature #0"] + noise[:, 0] > 0, xor["Feature #1"] + noise[:, 1] > 0
)
X = xor[feature_names]
y = target_xor.astype(np.int32)
fig, ax = plt.subplots()
ax.scatter(X["Feature #0"], X["Feature #1"], c=y, **common_scatter_plot_params)
ax.set_title("The XOR dataset")
plt.show()
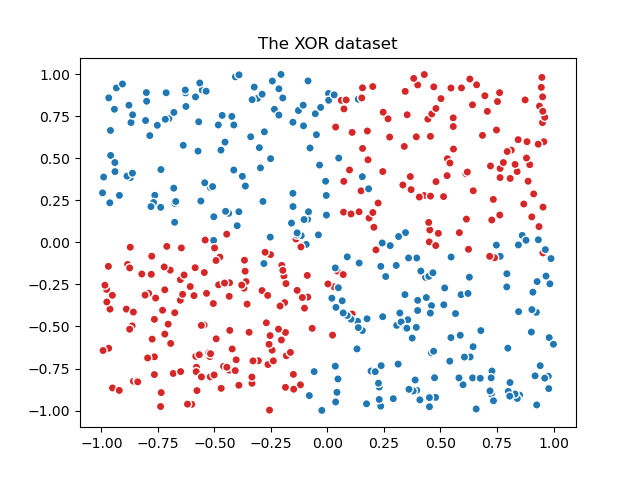
Aufgrund der inhärenten nichtlinearen Trennbarkeit des XOR-Datensatzes wären baumbasierte Modelle oft vorzuziehen. Angemessenes Feature Engineering in Kombination mit einem linearen Modell kann jedoch effektive Ergebnisse liefern, mit dem zusätzlichen Vorteil, besser kalibrierte Wahrscheinlichkeiten für Stichproben zu erzeugen, die sich in Übergangsregionen befinden, die von Rauschen beeinflusst werden.
Wir definieren und trainieren die Modelle auf dem gesamten Datensatz.
from sklearn.ensemble import VotingClassifier
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, SplineTransformer, StandardScaler
clf1 = make_pipeline(
SplineTransformer(degree=2, n_knots=2),
PolynomialFeatures(interaction_only=True),
LogisticRegression(C=10),
)
clf2 = make_pipeline(
SplineTransformer(
degree=2,
n_knots=4,
extrapolation="periodic",
include_bias=True,
),
PolynomialFeatures(interaction_only=True),
LogisticRegression(C=10),
)
clf3 = make_pipeline(
StandardScaler(),
Nystroem(gamma=2, random_state=0),
LogisticRegression(C=10),
)
weights = [2, 1, 3]
eclf = VotingClassifier(
estimators=[
("constant splines model", clf1),
("periodic splines model", clf2),
("nystroem model", clf3),
],
voting="soft",
weights=weights,
)
clf1.fit(X, y)
clf2.fit(X, y)
clf3.fit(X, y)
eclf.fit(X, y)
Schließlich verwenden wir DecisionBoundaryDisplay, um die vorhergesagten Wahrscheinlichkeiten darzustellen. Durch die Verwendung einer divergierenden Colormap (wie z. B. "RdBu") können wir sicherstellen, dass dunklere Farben einer `predict_proba` nahe 0 oder 1 entsprechen und Weiß einer `predict_proba` von 0,5 entspricht.
from itertools import product
from sklearn.inspection import DecisionBoundaryDisplay
fig, axarr = plt.subplots(2, 2, sharex="col", sharey="row", figsize=(10, 8))
for idx, clf, title in zip(
product([0, 1], [0, 1]),
[clf1, clf2, clf3, eclf],
[
"Splines with\nconstant extrapolation",
"Splines with\nperiodic extrapolation",
"RBF Nystroem",
"Soft Voting",
],
):
disp = DecisionBoundaryDisplay.from_estimator(
clf,
X,
response_method="predict_proba",
plot_method="pcolormesh",
cmap="RdBu",
alpha=0.8,
ax=axarr[idx[0], idx[1]],
)
axarr[idx[0], idx[1]].scatter(
X["Feature #0"],
X["Feature #1"],
c=y,
**common_scatter_plot_params,
)
axarr[idx[0], idx[1]].set_title(title)
fig.colorbar(disp.surface_, ax=axarr[idx[0], idx[1]], label="Probability estimate")
plt.show()

Als Plausibilitätsprüfung können wir für eine gegebene Stichprobe überprüfen, ob die vom VotingClassifier vorhergesagte Wahrscheinlichkeit tatsächlich die gewichtete Mittelung der Soft-Vorhersagen der einzelnen Klassifikatoren ist.
Im Fall der binären Klassifizierung, wie im vorliegenden Beispiel, enthalten die Arrays von predict_proba die Wahrscheinlichkeit, zu Klasse 0 zu gehören (hier in Rot) als ersten Eintrag und die Wahrscheinlichkeit, zu Klasse 1 zu gehören (hier in Blau) als zweiten Eintrag.
test_sample = pd.DataFrame({"Feature #0": [-0.5], "Feature #1": [1.5]})
predict_probas = [est.predict_proba(test_sample).ravel() for est in eclf.estimators_]
for (est_name, _), est_probas in zip(eclf.estimators, predict_probas):
print(f"{est_name}'s predicted probabilities: {est_probas}")
constant splines model's predicted probabilities: [0.11272662 0.88727338]
periodic splines model's predicted probabilities: [0.99726573 0.00273427]
nystroem model's predicted probabilities: [0.3185838 0.6814162]
Weighted average of soft-predictions: [0.3630784 0.6369216]
Wir können sehen, dass die manuelle Berechnung der vorherigen vorhergesagten Wahrscheinlichkeiten äquivalent zu der ist, die vom VotingClassifier erzeugt wird.
print(
"Predicted probability of VotingClassifier: "
f"{eclf.predict_proba(test_sample).ravel()}"
)
Predicted probability of VotingClassifier: [0.3630784 0.6369216]
Um Soft-Vorhersagen in Hard-Vorhersagen umzuwandeln, wenn Gewichte angegeben sind, werden die gewichteten durchschnittlichen vorhergesagten Wahrscheinlichkeiten für jede Klasse berechnet. Dann wird das endgültige Klassenlabel aus dem Klassenlabel mit der höchsten durchschnittlichen Wahrscheinlichkeit abgeleitet, was im Fall der binären Klassifizierung dem Standardgrenzwert von predict_proba=0.5 entspricht.
Class with the highest weighted average of soft-predictions: 1
Dies ist äquivalent zur Ausgabe der `predict`-Methode des VotingClassifier.
print(f"Predicted class of VotingClassifier: {eclf.predict(test_sample).ravel()}")
Predicted class of VotingClassifier: [1]
Soft-Votes können wie bei jedem anderen probabilistischen Klassifikator mit einem Schwellenwert versehen werden. Dies ermöglicht es Ihnen, einen Schwellenwert festzulegen, bei dem die positive Klasse vorhergesagt wird, anstatt einfach die Klasse mit der höchsten vorhergesagten Wahrscheinlichkeit auszuwählen.
from sklearn.model_selection import FixedThresholdClassifier
eclf_other_threshold = FixedThresholdClassifier(
eclf, threshold=0.7, response_method="predict_proba"
).fit(X, y)
print(
"Predicted class of thresholded VotingClassifier: "
f"{eclf_other_threshold.predict(test_sample)}"
)
Predicted class of thresholded VotingClassifier: [0]
Gesamtlaufzeit des Skripts: (0 Minuten 0,560 Sekunden)
Verwandte Beispiele
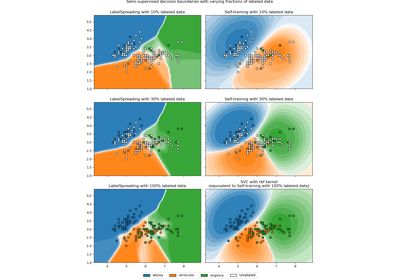
Entscheidungsgrenze semi-überwachter Klassifikatoren vs. SVM auf dem Iris-Datensatz