Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Precision-Recall#
Beispiel für die Precision-Recall-Metrik zur Bewertung der Qualität von Klassifikator-Ausgaben.
Precision-Recall ist ein nützliches Maß für den Erfolg einer Vorhersage, wenn die Klassen sehr unausgewogen sind. In der Information Retrieval ist Präzision ein Maß für den Anteil relevanter Elemente unter den tatsächlich zurückgegebenen Elementen, während Recall ein Maß für den Anteil der zurückgegebenen Elemente unter allen Elementen ist, die zurückgegeben hätten werden sollen. „Relevanz“ bezieht sich hier auf Elemente mit positivem Label, d. h. True Positives und False Positives.
Präzision (\(P\)) ist definiert als die Anzahl der True Positives (\(T_p\)) geteilt durch die Summe aus True Positives und False Positives (\(F_p\)).
Recall (\(R\)) ist definiert als die Anzahl der True Positives (\(T_p\)) geteilt durch die Summe aus True Positives und False Negatives (\(F_n\)).
Die Precision-Recall-Kurve zeigt den Kompromiss zwischen Präzision und Recall für verschiedene Schwellenwerte. Ein hoher Flächeninhalt unter der Kurve repräsentiert sowohl einen hohen Recall als auch eine hohe Präzision. Hohe Präzision wird erreicht, indem wenige False Positives in den zurückgegebenen Ergebnissen vorhanden sind, und hoher Recall wird erreicht, indem wenige False Negatives in den relevanten Ergebnissen vorhanden sind. Hohe Werte für beides zeigen, dass der Klassifikator genaue Ergebnisse liefert (hohe Präzision) und gleichzeitig die Mehrheit aller relevanten Ergebnisse zurückgibt (hoher Recall).
Ein System mit hohem Recall, aber niedriger Präzision gibt die meisten relevanten Elemente zurück, aber der Anteil der falsch gelabelten zurückgegebenen Ergebnisse ist hoch. Ein System mit hoher Präzision, aber niedrigem Recall ist genau das Gegenteil: Es gibt nur sehr wenige der relevanten Elemente zurück, aber die meisten seiner vorhergesagten Labels sind korrekt, wenn sie mit den tatsächlichen Labels verglichen werden. Ein ideales System mit hoher Präzision und hohem Recall gibt die meisten relevanten Elemente zurück, wobei die meisten Ergebnisse korrekt gelabelt sind.
Die Definition der Präzision (\(\frac{T_p}{T_p + F_p}\)) zeigt, dass eine Absenkung des Schwellenwerts eines Klassifikators den Nenner erhöhen kann, indem die Anzahl der zurückgegebenen Ergebnisse erhöht wird. Wenn der Schwellenwert zuvor zu hoch eingestellt war, können die neuen Ergebnisse alle True Positives sein, was die Präzision erhöht. Wenn der vorherige Schwellenwert etwa richtig oder zu niedrig war, führt eine weitere Absenkung des Schwellenwerts zu False Positives, was die Präzision verringert.
Recall ist definiert als \(\frac{T_p}{T_p+F_n}\), wobei \(T_p+F_n\) nicht vom Klassifikator-Schwellenwert abhängt. Eine Änderung des Klassifikator-Schwellenwerts kann nur den Zähler, \(T_p\), ändern. Eine Absenkung des Klassifikator-Schwellenwerts kann den Recall erhöhen, indem die Anzahl der True Positive Ergebnisse erhöht wird. Es ist auch möglich, dass eine Absenkung des Schwellenwerts den Recall unverändert lässt, während die Präzision schwankt. Daher nimmt die Präzision nicht zwangsläufig mit dem Recall ab.
Die Beziehung zwischen Recall und Präzision kann im Treppenbereich des Plots beobachtet werden – an den Kanten dieser Stufen reduziert eine kleine Änderung des Schwellenwerts die Präzision erheblich, mit nur einem geringen Gewinn an Recall.
Average Precision (AP) fasst einen solchen Plot als gewichteten Mittelwert der Präzisionen zusammen, die bei jedem Schwellenwert erzielt werden, wobei die Erhöhung des Recalls gegenüber dem vorherigen Schwellenwert als Gewicht verwendet wird.
\(\text{AP} = \sum_n (R_n - R_{n-1}) P_n\)
wobei \(P_n\) und \(R_n\) Präzision und Recall beim n-ten Schwellenwert sind. Ein Paar \((R_k, P_k)\) wird als Betriebspunkt bezeichnet.
AP und die trapezförmige Fläche unter den Betriebspunkten (sklearn.metrics.auc) sind gängige Methoden zur Zusammenfassung einer Precision-Recall-Kurve, die zu unterschiedlichen Ergebnissen führen. Lesen Sie mehr im Benutzerhandbuch.
Precision-Recall-Kurven werden typischerweise in der binären Klassifizierung verwendet, um die Ausgabe eines Klassifikators zu untersuchen. Um die Precision-Recall-Kurve und die Average Precision auf die Multi-Klassen- oder Multi-Label-Klassifizierung zu erweitern, ist es notwendig, die Ausgabe zu binarisieren. Eine Kurve kann pro Label gezeichnet werden, aber man kann auch eine Precision-Recall-Kurve zeichnen, indem jedes Element der Label-Indikator-Matrix als binäre Vorhersage betrachtet wird (Mikro-Mittelwertbildung).
Hinweis
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
In binären Klassifizierungsszenarien#
Datensatz und Modell#
Wir verwenden einen Linear SVC-Klassifikator, um zwei Arten von Schwertlilien zu unterscheiden.
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
X, y = load_iris(return_X_y=True)
# Add noisy features
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)
# Limit to the two first classes, and split into training and test
X_train, X_test, y_train, y_test = train_test_split(
X[y < 2], y[y < 2], test_size=0.5, random_state=random_state
)
Linear SVC erwartet, dass jedes Merkmal einen ähnlichen Wertebereich hat. Daher werden wir die Daten zuerst mit einem StandardScaler skalieren.
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
classifier = make_pipeline(StandardScaler(), LinearSVC(random_state=random_state))
classifier.fit(X_train, y_train)
Plotten der Precision-Recall-Kurve#
Um die Precision-Recall-Kurve zu zeichnen, sollten Sie PrecisionRecallDisplay verwenden. Tatsächlich gibt es zwei verfügbare Methoden, je nachdem, ob Sie die Vorhersagen des Klassifikators bereits berechnet haben oder nicht.
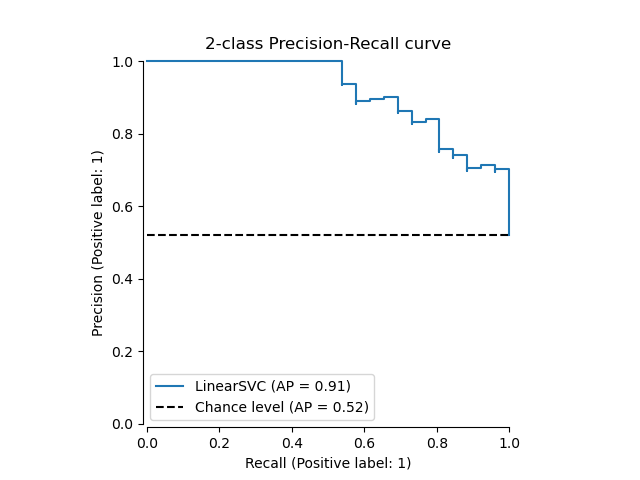
Lassen Sie uns zuerst die Precision-Recall-Kurve ohne die Klassifikator-Vorhersagen zeichnen. Wir verwenden from_estimator, die die Vorhersagen für uns berechnet, bevor die Kurve gezeichnet wird.
from sklearn.metrics import PrecisionRecallDisplay
display = PrecisionRecallDisplay.from_estimator(
classifier, X_test, y_test, name="LinearSVC", plot_chance_level=True, despine=True
)
_ = display.ax_.set_title("2-class Precision-Recall curve")
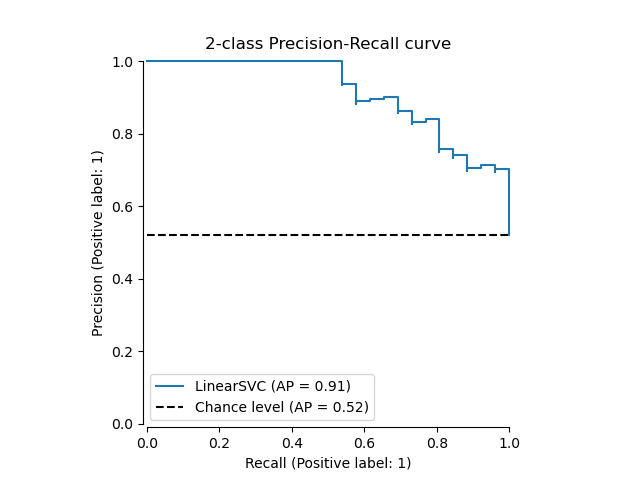
Wenn wir bereits die geschätzten Wahrscheinlichkeiten oder Scores für unser Modell haben, können wir from_predictions verwenden.
y_score = classifier.decision_function(X_test)
display = PrecisionRecallDisplay.from_predictions(
y_test, y_score, name="LinearSVC", plot_chance_level=True, despine=True
)
_ = display.ax_.set_title("2-class Precision-Recall curve")
In Multi-Label-Einstellungen#
Die Precision-Recall-Kurve unterstützt nicht das Multi-Label-Setting. Man kann jedoch entscheiden, wie man diesen Fall behandelt. Wir zeigen unten ein solches Beispiel.
Erstellen von Multi-Label-Daten, Anpassen und Vorhersagen#
Wir erstellen einen Multi-Label-Datensatz, um die Präzision-Recall in Multi-Label-Einstellungen zu illustrieren.
from sklearn.preprocessing import label_binarize
# Use label_binarize to be multi-label like settings
Y = label_binarize(y, classes=[0, 1, 2])
n_classes = Y.shape[1]
# Split into training and test
X_train, X_test, Y_train, Y_test = train_test_split(
X, Y, test_size=0.5, random_state=random_state
)
Wir verwenden OneVsRestClassifier für Multi-Label-Vorhersagen.
from sklearn.multiclass import OneVsRestClassifier
classifier = OneVsRestClassifier(
make_pipeline(StandardScaler(), LinearSVC(random_state=random_state))
)
classifier.fit(X_train, Y_train)
y_score = classifier.decision_function(X_test)
Der Average Precision Score in Multi-Label-Einstellungen#
from sklearn.metrics import average_precision_score, precision_recall_curve
# For each class
precision = dict()
recall = dict()
average_precision = dict()
for i in range(n_classes):
precision[i], recall[i], _ = precision_recall_curve(Y_test[:, i], y_score[:, i])
average_precision[i] = average_precision_score(Y_test[:, i], y_score[:, i])
# A "micro-average": quantifying score on all classes jointly
precision["micro"], recall["micro"], _ = precision_recall_curve(
Y_test.ravel(), y_score.ravel()
)
average_precision["micro"] = average_precision_score(Y_test, y_score, average="micro")
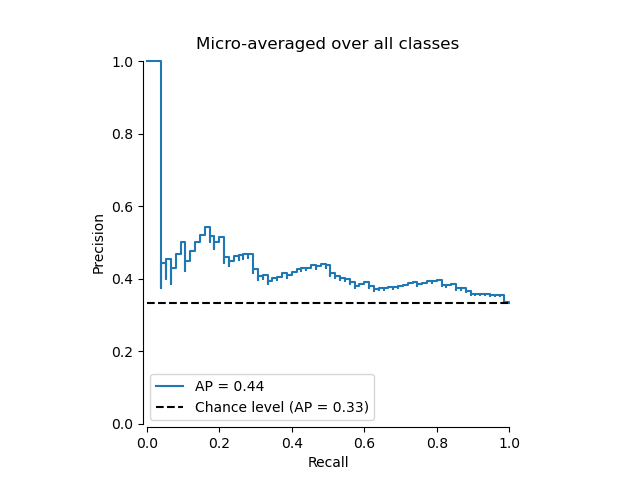
Plotten der mikro-gemittelten Precision-Recall-Kurve#
from collections import Counter
display = PrecisionRecallDisplay(
recall=recall["micro"],
precision=precision["micro"],
average_precision=average_precision["micro"],
prevalence_pos_label=Counter(Y_test.ravel())[1] / Y_test.size,
)
display.plot(plot_chance_level=True, despine=True)
_ = display.ax_.set_title("Micro-averaged over all classes")
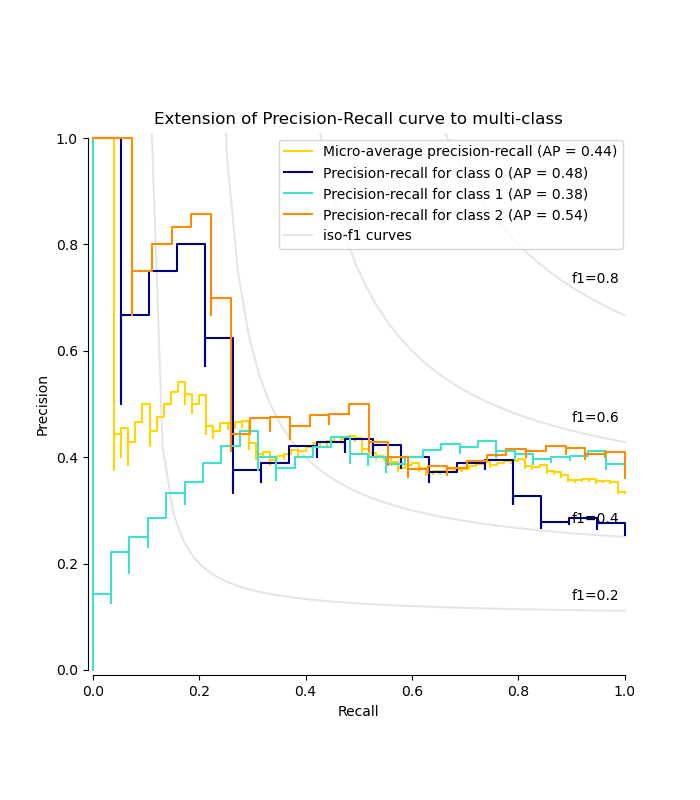
Plotten der Precision-Recall-Kurve für jede Klasse und Iso-F1-Kurven#
from itertools import cycle
import matplotlib.pyplot as plt
# setup plot details
colors = cycle(["navy", "turquoise", "darkorange", "cornflowerblue", "teal"])
_, ax = plt.subplots(figsize=(7, 8))
f_scores = np.linspace(0.2, 0.8, num=4)
lines, labels = [], []
for f_score in f_scores:
x = np.linspace(0.01, 1)
y = f_score * x / (2 * x - f_score)
(l,) = plt.plot(x[y >= 0], y[y >= 0], color="gray", alpha=0.2)
plt.annotate("f1={0:0.1f}".format(f_score), xy=(0.9, y[45] + 0.02))
display = PrecisionRecallDisplay(
recall=recall["micro"],
precision=precision["micro"],
average_precision=average_precision["micro"],
)
display.plot(ax=ax, name="Micro-average precision-recall", color="gold")
for i, color in zip(range(n_classes), colors):
display = PrecisionRecallDisplay(
recall=recall[i],
precision=precision[i],
average_precision=average_precision[i],
)
display.plot(
ax=ax, name=f"Precision-recall for class {i}", color=color, despine=True
)
# add the legend for the iso-f1 curves
handles, labels = display.ax_.get_legend_handles_labels()
handles.extend([l])
labels.extend(["iso-f1 curves"])
# set the legend and the axes
ax.legend(handles=handles, labels=labels, loc="best")
ax.set_title("Extension of Precision-Recall curve to multi-class")
plt.show()
Gesamtlaufzeit des Skripts: (0 Minuten 2,113 Sekunden)
Verwandte Beispiele

Benutzerdefinierte Refit-Strategie einer Gitter-Suche mit Kreuzvalidierung
Post-Hoc-Anpassung des Entscheidungsschwellenwerts für kostenempfindliches Lernen