Gaußsche Mischmodell-Sinuskurve

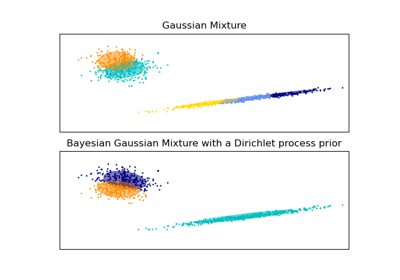
Dieses Beispiel demonstriert das Verhalten von Gaußschen Mischmodellen, die auf Daten angewendet werden, welche nicht aus einer Mischung von Gaußschen Zufallsvariablen gezogen wurden. Der Datensatz besteht aus 100 Punkten, die lose einer verrauschten Sinuskurve folgend angeordnet sind. Es gibt daher keinen "Ground Truth"-Wert für die Anzahl der Gaußschen Komponenten.

Das erste Modell ist ein klassisches Gaußsches Mischmodell mit 10 Komponenten, das mit dem Erwartungsmaximierungsalgorithmus angepasst wird.

Das zweite Modell ist ein Bayes'sches Gaußsches Mischmodell mit einem Dirichlet-Prozess-Prior, das mit Variationsinferenz angepasst wird. Der niedrige Wert des Konzentrationspriors veranlasst das Modell, eine geringere Anzahl aktiver Komponenten zu bevorzugen. Dieses Modell "entscheidet" sich, seine Modellierungskraft auf das Gesamtbild der Struktur des Datensatzes zu konzentrieren: Gruppen von Punkten mit abwechselnden Richtungen, die durch nicht-diagonale Kovarianzmatrizen modelliert werden. Diese abwechselnden Richtungen erfassen ungefähr die abwechselnde Natur des ursprünglichen Sinussignals.

Das dritte Modell ist ebenfalls ein Bayes'sches Gaußsches Mischmodell mit einem Dirichlet-Prozess-Prior, aber dieses Mal ist der Wert des Konzentrationspriors höher, was dem Modell mehr Freiheit gibt, die feingranulare Struktur der Daten zu modellieren. Das Ergebnis ist eine Mischung mit einer größeren Anzahl aktiver Komponenten, ähnlich dem ersten Modell, bei dem wir willkürlich die Anzahl der Komponenten auf 10 festgelegt haben.

Welches Modell das beste ist, ist eine Frage des subjektiven Urteils: Möchten wir Modelle bevorzugen, die nur das Gesamtbild erfassen, um den Großteil der Datenstruktur zusammenzufassen und zu erklären, während Details ignoriert werden, oder bevorzugen wir Modelle, die den Dichtebereichen des Signals genau folgen?

Die letzten beiden Panels zeigen, wie wir aus den letzten beiden Modellen sampeln können. Die resultierenden Stichprobenverteilungen sehen nicht exakt wie die ursprüngliche Datenverteilung aus. Der Unterschied ergibt sich hauptsächlich aus dem Approximationsfehler, den wir gemacht haben, indem wir ein Modell verwendet haben, das davon ausgeht, dass die Daten von einer endlichen Anzahl von Gaußschen Komponenten generiert wurden, anstatt von einer kontinuierlichen verrauschten Sinuskurve.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import itertools

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg

from sklearn import mixture

color_iter = itertools.cycle(["navy", "c", "cornflowerblue", "gold", "darkorange"])


def plot_results(X, Y, means, covariances, index, title):
    splot = plt.subplot(5, 1, 1 + index)
    for i, (mean, covar, color) in enumerate(zip(means, covariances, color_iter)):
        v, w = linalg.eigh(covar)
        v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
        u = w[0] / linalg.norm(w[0])
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y == i):
            continue
        plt.scatter(X[Y == i, 0], X[Y == i, 1], 0.8, color=color)

        # Plot an ellipse to show the Gaussian component
        angle = np.arctan(u[1] / u[0])
        angle = 180.0 * angle / np.pi  # convert to degrees
        ell = mpl.patches.Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
        ell.set_clip_box(splot.bbox)
        ell.set_alpha(0.5)
        splot.add_artist(ell)

    plt.xlim(-6.0, 4.0 * np.pi - 6.0)
    plt.ylim(-5.0, 5.0)
    plt.title(title)
    plt.xticks(())
    plt.yticks(())


def plot_samples(X, Y, n_components, index, title):
    plt.subplot(5, 1, 4 + index)
    for i, color in zip(range(n_components), color_iter):
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y == i):
            continue
        plt.scatter(X[Y == i, 0], X[Y == i, 1], 0.8, color=color)

    plt.xlim(-6.0, 4.0 * np.pi - 6.0)
    plt.ylim(-5.0, 5.0)
    plt.title(title)
    plt.xticks(())
    plt.yticks(())


# Parameters
n_samples = 100

# Generate random sample following a sine curve
np.random.seed(0)
X = np.zeros((n_samples, 2))
step = 4.0 * np.pi / n_samples

for i in range(X.shape[0]):
    x = i * step - 6.0
    X[i, 0] = x + np.random.normal(0, 0.1)
    X[i, 1] = 3.0 * (np.sin(x) + np.random.normal(0, 0.2))

plt.figure(figsize=(10, 10))
plt.subplots_adjust(
    bottom=0.04, top=0.95, hspace=0.2, wspace=0.05, left=0.03, right=0.97
)

# Fit a Gaussian mixture with EM using ten components
gmm = mixture.GaussianMixture(
    n_components=10, covariance_type="full", max_iter=100
).fit(X)
plot_results(
    X, gmm.predict(X), gmm.means_, gmm.covariances_, 0, "Expectation-maximization"
)

dpgmm = mixture.BayesianGaussianMixture(
    n_components=10,
    covariance_type="full",
    weight_concentration_prior=1e-2,
    weight_concentration_prior_type="dirichlet_process",
    mean_precision_prior=1e-2,
    covariance_prior=1e0 * np.eye(2),
    init_params="random",
    max_iter=100,
    random_state=2,
).fit(X)
plot_results(
    X,
    dpgmm.predict(X),
    dpgmm.means_,
    dpgmm.covariances_,
    1,
    "Bayesian Gaussian mixture models with a Dirichlet process prior "
    r"for $\gamma_0=0.01$.",
)

X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(
    X_s,
    y_s,
    dpgmm.n_components,
    0,
    "Gaussian mixture with a Dirichlet process prior "
    r"for $\gamma_0=0.01$ sampled with $2000$ samples.",
)

dpgmm = mixture.BayesianGaussianMixture(
    n_components=10,
    covariance_type="full",
    weight_concentration_prior=1e2,
    weight_concentration_prior_type="dirichlet_process",
    mean_precision_prior=1e-2,
    covariance_prior=1e0 * np.eye(2),
    init_params="kmeans",
    max_iter=100,
    random_state=2,
).fit(X)
plot_results(
    X,
    dpgmm.predict(X),
    dpgmm.means_,
    dpgmm.covariances_,
    2,
    "Bayesian Gaussian mixture models with a Dirichlet process prior "
    r"for $\gamma_0=100$",
)

X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(
    X_s,
    y_s,
    dpgmm.n_components,
    1,
    "Gaussian mixture with a Dirichlet process prior "
    r"for $\gamma_0=100$ sampled with $2000$ samples.",
)

plt.show()

Verwandte Beispiele

Gaußsche Mischmodell-Ellipsoide

Gaußsche Mischmodell-Ellipsoide

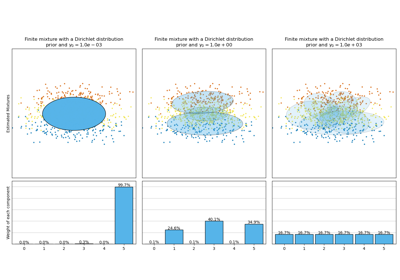
Analyse des Konzentrations-Prior-Typs der Variation im Bayes'schen Gaußschen Gemisch

Analyse des Konzentrations-Prior-Typs der Variation im Bayes'schen Gaußschen Gemisch

Dichteschätzung für ein Gaußsches Gemisch

Dichteschätzung für ein Gaußsches Gemisch

GMM Kovarianzen

GMM Kovarianzen