Hashing-Merkmalstransformation mittels Totally Random Trees

RandomTreesEmbedding bietet eine Möglichkeit, Daten in eine sehr hochdimensionale, spärliche Darstellung abzubilden, was für die Klassifizierung vorteilhaft sein kann. Die Abbildung ist vollständig unüberwacht und sehr effizient.

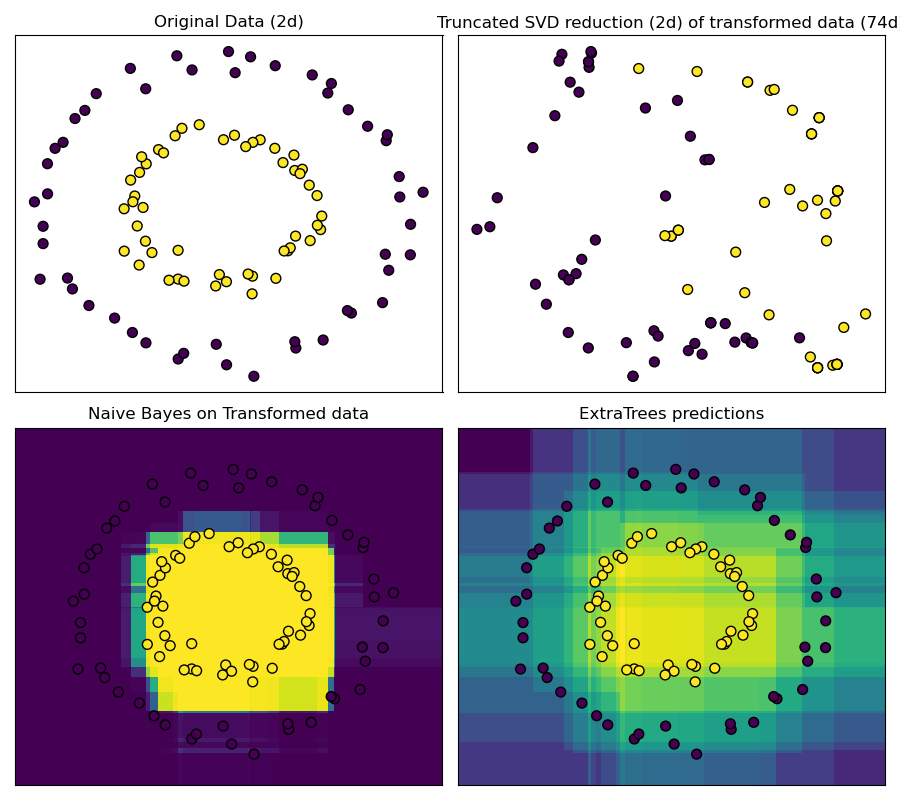
Dieses Beispiel visualisiert die durch mehrere Bäume gegebenen Partitionen und zeigt, wie die Transformation auch für nichtlineare Dimensionsreduktion oder nichtlineare Klassifizierung verwendet werden kann.

Benachbarte Punkte teilen sich oft denselben Blattknoten eines Baumes und teilen daher große Teile ihrer Hashed-Darstellung. Dies ermöglicht die Trennung zweier konzentrischer Kreise, einfach basierend auf den Hauptkomponenten der transformierten Daten mit abgeschnittenem SVD.

In hochdimensionalen Räumen erzielen lineare Klassifikatoren oft eine ausgezeichnete Genauigkeit. Für spärliche binäre Daten ist BernoulliNB besonders gut geeignet. Die unterste Reihe vergleicht die durch BernoulliNB im transformierten Raum erhaltene Entscheidungsgrenze mit einem ExtraTreesClassifier-Wald, der auf den Originaldaten gelernt wurde.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_circles
from sklearn.decomposition import TruncatedSVD
from sklearn.ensemble import ExtraTreesClassifier, RandomTreesEmbedding
from sklearn.naive_bayes import BernoulliNB

# make a synthetic dataset
X, y = make_circles(factor=0.5, random_state=0, noise=0.05)

# use RandomTreesEmbedding to transform data
hasher = RandomTreesEmbedding(n_estimators=10, random_state=0, max_depth=3)
X_transformed = hasher.fit_transform(X)

# Visualize result after dimensionality reduction using truncated SVD
svd = TruncatedSVD(n_components=2)
X_reduced = svd.fit_transform(X_transformed)

# Learn a Naive Bayes classifier on the transformed data
nb = BernoulliNB()
nb.fit(X_transformed, y)


# Learn an ExtraTreesClassifier for comparison
trees = ExtraTreesClassifier(max_depth=3, n_estimators=10, random_state=0)
trees.fit(X, y)


# scatter plot of original and reduced data
fig = plt.figure(figsize=(9, 8))

ax = plt.subplot(221)
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_title("Original Data (2d)")
ax.set_xticks(())
ax.set_yticks(())

ax = plt.subplot(222)
ax.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, s=50, edgecolor="k")
ax.set_title(
    "Truncated SVD reduction (2d) of transformed data (%dd)" % X_transformed.shape[1]
)
ax.set_xticks(())
ax.set_yticks(())

# Plot the decision in original space. For that, we will assign a color
# to each point in the mesh [x_min, x_max]x[y_min, y_max].
h = 0.01
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

# transform grid using RandomTreesEmbedding
transformed_grid = hasher.transform(np.c_[xx.ravel(), yy.ravel()])
y_grid_pred = nb.predict_proba(transformed_grid)[:, 1]

ax = plt.subplot(223)
ax.set_title("Naive Bayes on Transformed data")
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

# transform grid using ExtraTreesClassifier
y_grid_pred = trees.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]

ax = plt.subplot(224)
ax.set_title("ExtraTrees predictions")
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

plt.tight_layout()
plt.show()

Verwandte Beispiele

Variierende Regularisierung im Multi-Layer Perceptron

Variierende Regularisierung im Multi-Layer Perceptron

Gauß-Prozess-Klassifikation (GPC) auf dem Iris-Datensatz

Gauß-Prozess-Klassifikation (GPC) auf dem Iris-Datensatz

Merkmalsdiskretisierung

Merkmalsdiskretisierung

SVM-Randbeispiel

SVM-Randbeispiel