Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Kernel PCA#
Dieses Beispiel zeigt den Unterschied zwischen der Principal Component Analysis (PCA) (PCA) und ihrer kernelisierten Version (KernelPCA).
Einerseits zeigen wir, dass KernelPCA in der Lage ist, eine Projektion der Daten zu finden, die diese linear trennt, während dies mit PCA nicht der Fall ist.
Schließlich zeigen wir, dass die Umkehrung dieser Projektion bei KernelPCA eine Annäherung ist, während sie bei PCA exakt ist.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Daten projizieren: PCA vs. KernelPCA#
In diesem Abschnitt zeigen wir die Vorteile der Verwendung eines Kernels bei der Projektion von Daten mittels Principal Component Analysis (PCA). Wir erstellen einen Datensatz, der aus zwei verschachtelten Kreisen besteht.
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
X, y = make_circles(n_samples=1_000, factor=0.3, noise=0.05, random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)
Betrachten wir zunächst den generierten Datensatz.
import matplotlib.pyplot as plt
_, (train_ax, test_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(8, 4))
train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train)
train_ax.set_ylabel("Feature #1")
train_ax.set_xlabel("Feature #0")
train_ax.set_title("Training data")
test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
test_ax.set_xlabel("Feature #0")
_ = test_ax.set_title("Testing data")
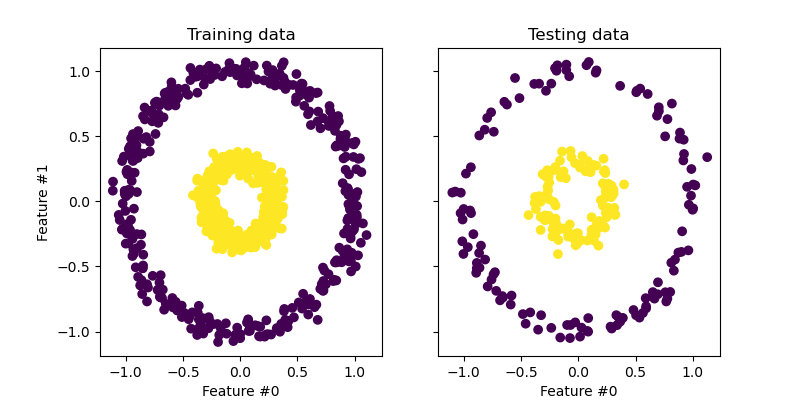
Die Stichproben jeder Klasse können nicht linear getrennt werden: Es gibt keine gerade Linie, die die Stichproben des inneren Satzes von denen des äußeren Satzes trennen kann.
Nun verwenden wir PCA mit und ohne Kernel, um die Auswirkung der Verwendung eines solchen Kernels zu sehen. Der hier verwendete Kernel ist ein Radial Basis Function (RBF) Kernel.
fig, (orig_data_ax, pca_proj_ax, kernel_pca_proj_ax) = plt.subplots(
ncols=3, figsize=(14, 4)
)
orig_data_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
orig_data_ax.set_ylabel("Feature #1")
orig_data_ax.set_xlabel("Feature #0")
orig_data_ax.set_title("Testing data")
pca_proj_ax.scatter(X_test_pca[:, 0], X_test_pca[:, 1], c=y_test)
pca_proj_ax.set_ylabel("Principal component #1")
pca_proj_ax.set_xlabel("Principal component #0")
pca_proj_ax.set_title("Projection of testing data\n using PCA")
kernel_pca_proj_ax.scatter(X_test_kernel_pca[:, 0], X_test_kernel_pca[:, 1], c=y_test)
kernel_pca_proj_ax.set_ylabel("Principal component #1")
kernel_pca_proj_ax.set_xlabel("Principal component #0")
_ = kernel_pca_proj_ax.set_title("Projection of testing data\n using KernelPCA")

Wir erinnern uns, dass PCA die Daten linear transformiert. Intuitiv bedeutet dies, dass das Koordinatensystem zentriert, auf jeder Komponente im Verhältnis zu ihrer Varianz skaliert und schließlich rotiert wird. Die durch diese Transformation erhaltenen Daten sind isotrop und können nun auf ihre Hauptkomponenten projiziert werden.
Somit sehen wir bei Betrachtung der durch PCA erzeugten Projektion (d.h. der mittleren Abbildung), dass sich hinsichtlich der Skalierung nichts ändert; da die Daten zwei konzentrische Kreise sind, die um Null zentriert sind, sind die ursprünglichen Daten bereits isotrop. Wir können jedoch sehen, dass die Daten rotiert wurden. Abschließend lässt sich sagen, dass eine solche Projektion nicht hilfreich wäre, wenn man einen linearen Klassifikator definieren möchte, um Stichproben beider Klassen zu unterscheiden.
Die Verwendung eines Kernels ermöglicht eine nicht-lineare Projektion. Hier erwarten wir durch die Verwendung eines RBF-Kernels, dass die Projektion den Datensatz entfaltet und dabei die relativen Abstände von Paaren von Datenpunkten, die im ursprünglichen Raum nahe beieinander liegen, ungefähr beibehält.
Wir beobachten dieses Verhalten auf der Abbildung rechts: Die Stichproben einer bestimmten Klasse liegen näher beieinander als die Stichproben der gegenüberliegenden Klasse, wodurch beide Stichprobensätze entwirrt werden. Nun können wir einen linearen Klassifikator verwenden, um die Stichproben der beiden Klassen zu trennen.
Projektion in den ursprünglichen Merkmalsraum#
Eine Besonderheit, die man bei der Verwendung von KernelPCA beachten sollte, betrifft die Rekonstruktion (d.h. die Rückprojektion in den ursprünglichen Merkmalsraum). Bei PCA ist die Rekonstruktion exakt, wenn n_components der Anzahl der ursprünglichen Merkmale entspricht. Dies ist in diesem Beispiel der Fall.
Wir können untersuchen, ob wir den ursprünglichen Datensatz erhalten, wenn wir mit KernelPCA zurückprojizieren.
X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test))
X_reconstructed_kernel_pca = kernel_pca.inverse_transform(kernel_pca.transform(X_test))
fig, (orig_data_ax, pca_back_proj_ax, kernel_pca_back_proj_ax) = plt.subplots(
ncols=3, sharex=True, sharey=True, figsize=(13, 4)
)
orig_data_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
orig_data_ax.set_ylabel("Feature #1")
orig_data_ax.set_xlabel("Feature #0")
orig_data_ax.set_title("Original test data")
pca_back_proj_ax.scatter(X_reconstructed_pca[:, 0], X_reconstructed_pca[:, 1], c=y_test)
pca_back_proj_ax.set_xlabel("Feature #0")
pca_back_proj_ax.set_title("Reconstruction via PCA")
kernel_pca_back_proj_ax.scatter(
X_reconstructed_kernel_pca[:, 0], X_reconstructed_kernel_pca[:, 1], c=y_test
)
kernel_pca_back_proj_ax.set_xlabel("Feature #0")
_ = kernel_pca_back_proj_ax.set_title("Reconstruction via KernelPCA")
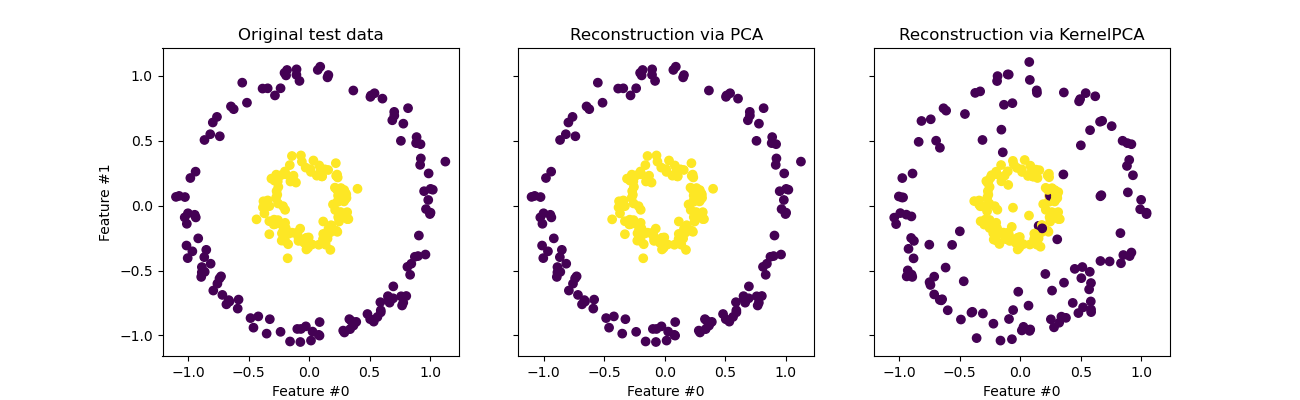
Während wir bei PCA eine perfekte Rekonstruktion sehen, beobachten wir bei KernelPCA ein anderes Ergebnis.
Tatsächlich kann inverse_transform nicht auf eine analytische Rückprojektion und somit auf eine exakte Rekonstruktion zurückgreifen. Stattdessen wird intern ein KernelRidge trainiert, um eine Abbildung von der kernelisierten PCA-Basis auf den ursprünglichen Merkmalsraum zu lernen. Diese Methode ist daher mit einer Annäherung verbunden, die kleine Unterschiede bei der Rückprojektion in den ursprünglichen Merkmalsraum einführt.
Um die Rekonstruktion mit inverse_transform zu verbessern, kann alpha in KernelPCA, der Regularisierungsterm, der die Abhängigkeit von den Trainingsdaten während des Trainings der Abbildung steuert, angepasst werden.
Gesamtlaufzeit des Skripts: (0 Minuten 0,508 Sekunden)
Verwandte Beispiele
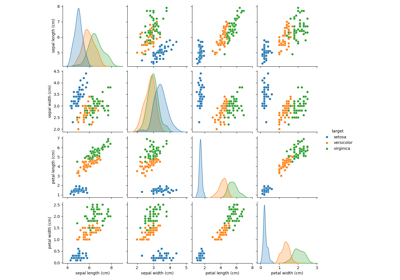
Principal Component Analysis (PCA) auf dem Iris-Datensatz