Skalierung des Regularisierungsparameters für SVCs

Das folgende Beispiel veranschaulicht die Auswirkung der Skalierung des Regularisierungsparameters bei der Verwendung von Support Vector Machines für die Klassifizierung. Für die SVC-Klassifizierung sind wir an einer Risikominimierung für die Gleichung interessiert

\[C \sum_{i=1, n} \mathcal{L} (f(x_i), y_i) + \Omega (w)\]

wobei

• \(C\) zur Festlegung des Regularisierungsbetrags verwendet wird

• \(\mathcal{L}\) eine Loss-Funktion unserer Stichproben und unserer Modellparameter ist.

• \(\Omega\) eine Penalty-Funktion unserer Modellparameter ist

Wenn wir die Loss-Funktion als den individuellen Fehler pro Stichprobe betrachten, dann steigt der Data-Fit-Term oder die Summe des Fehlers für jede Stichprobe, wenn wir mehr Stichproben hinzufügen. Der Straf-Term steigt jedoch nicht.

Bei der Verwendung von beispielsweise Kreuzvalidierung zur Festlegung des Regularisierungsbetrags mit C gäbe es eine unterschiedliche Anzahl von Stichproben zwischen dem Hauptproblem und den kleineren Problemen innerhalb der Folds der Kreuzvalidierung.

Da die Loss-Funktion vom Stichprobenumfang abhängt, beeinflusst letzterer den ausgewählten Wert von C. Die Frage, die sich stellt, ist: "Wie passen wir C optimal an, um den unterschiedlichen Umfang der Trainingsstichproben zu berücksichtigen?"

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datengenerierung

In diesem Beispiel untersuchen wir die Auswirkung der Neuparametrisierung des Regularisierungsparameters C, um die Anzahl der Stichproben bei Verwendung einer L1- oder L2-Strafe zu berücksichtigen. Zu diesem Zweck erstellen wir einen synthetischen Datensatz mit einer großen Anzahl von Merkmalen, von denen nur wenige informativ sind. Wir erwarten daher, dass die Regularisierung die Koeffizienten gegen Null (L2-Strafe) oder exakt Null (L1-Strafe) schrumpfen lässt.

from sklearn.datasets import make_classification

n_samples, n_features = 100, 300
X, y = make_classification(
    n_samples=n_samples, n_features=n_features, n_informative=5, random_state=1
)

L1-Strafen-Fall

Im L1-Fall besagt die Theorie, dass bei starker Regularisierung der Schätzer nicht so gut vorhersagen kann wie ein Modell, das die wahre Verteilung kennt (selbst im Limes, wo die Stichprobengröße gegen unendlich wächst), da er einige Gewichte von ansonsten prädiktiven Merkmalen auf Null setzen kann, was einen Bias induziert. Es besagt jedoch, dass es möglich ist, die richtige Menge an Nicht-Null-Parametern sowie deren Vorzeichen durch Abstimmung von C zu finden.

Wir definieren einen linearen SVC mit der L1-Strafe.

from sklearn.svm import LinearSVC

model_l1 = LinearSVC(penalty="l1", loss="squared_hinge", dual=False, tol=1e-3)

Wir berechnen den mittleren Test-Score für verschiedene Werte von C mittels Kreuzvalidierung.

import numpy as np
import pandas as pd

from sklearn.model_selection import ShuffleSplit, validation_curve

Cs = np.logspace(-2.3, -1.3, 10)
train_sizes = np.linspace(0.3, 0.7, 3)
labels = [f"fraction: {train_size}" for train_size in train_sizes]
shuffle_params = {
    "test_size": 0.3,
    "n_splits": 150,
    "random_state": 1,
}

results = {"C": Cs}
for label, train_size in zip(labels, train_sizes):
    cv = ShuffleSplit(train_size=train_size, **shuffle_params)
    train_scores, test_scores = validation_curve(
        model_l1,
        X,
        y,
        param_name="C",
        param_range=Cs,
        cv=cv,
        n_jobs=2,
    )
    results[label] = test_scores.mean(axis=1)
results = pd.DataFrame(results)

import matplotlib.pyplot as plt

fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(12, 6))

# plot results without scaling C
results.plot(x="C", ax=axes[0], logx=True)
axes[0].set_ylabel("CV score")
axes[0].set_title("No scaling")

for label in labels:
    best_C = results.loc[results[label].idxmax(), "C"]
    axes[0].axvline(x=best_C, linestyle="--", color="grey", alpha=0.7)

# plot results by scaling C
for train_size_idx, label in enumerate(labels):
    train_size = train_sizes[train_size_idx]
    results_scaled = results[[label]].assign(
        C_scaled=Cs * float(n_samples * np.sqrt(train_size))
    )
    results_scaled.plot(x="C_scaled", ax=axes[1], logx=True, label=label)
    best_C_scaled = results_scaled["C_scaled"].loc[results[label].idxmax()]
    axes[1].axvline(x=best_C_scaled, linestyle="--", color="grey", alpha=0.7)

axes[1].set_title("Scaling C by sqrt(1 / n_samples)")

_ = fig.suptitle("Effect of scaling C with L1 penalty")

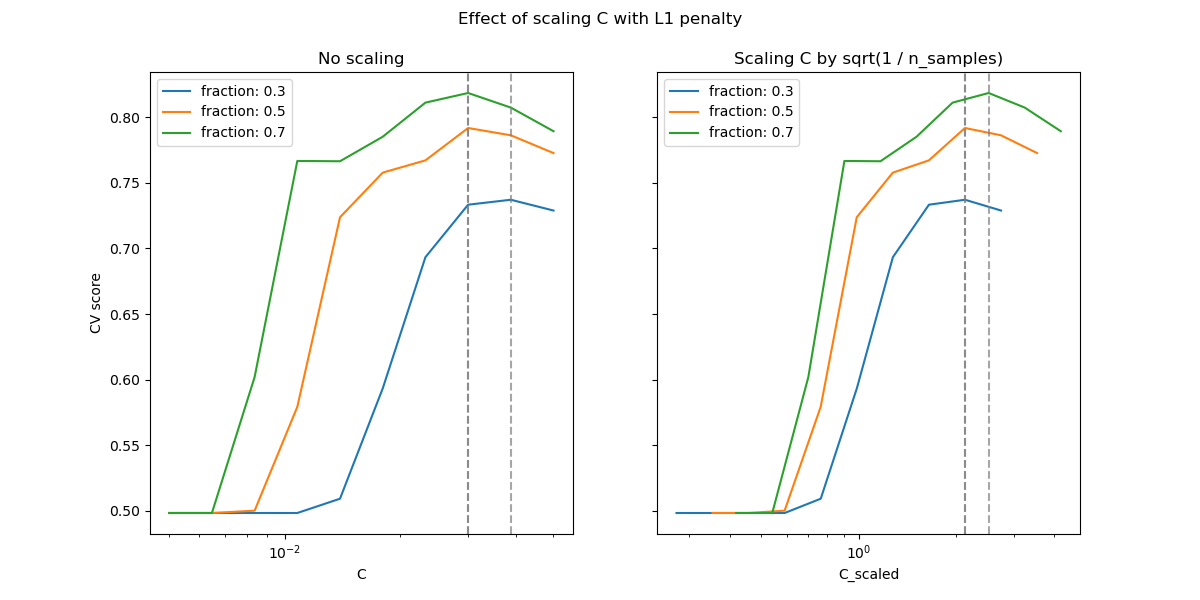
Im Bereich kleiner C (starke Regularisierung) sind alle von den Modellen gelernten Koeffizienten Null, was zu schwerem Underfitting führt. Tatsächlich liegt die Genauigkeit in diesem Bereich auf dem Zufallsniveau.

Die Verwendung der Standard-Skalierung führt zu einem einigermaßen stabilen optimalen Wert von C, während der Übergang aus der Underfitting-Region von der Anzahl der Trainingsstichproben abhängt. Die Neuparametrisierung führt zu noch stabileren Ergebnissen.

Siehe z.B. Theorem 3 von On the prediction performance of the Lasso oder Simultaneous analysis of Lasso and Dantzig selector, wo der Regularisierungsparameter immer als proportional zu 1 / sqrt(n_samples) angenommen wird.

L2-Strafen-Fall

Wir können ein ähnliches Experiment mit der L2-Strafe durchführen. In diesem Fall besagt die Theorie, dass zur Erzielung von Vorhersagekonsistenz der Strafparameter konstant gehalten werden sollte, wenn die Anzahl der Stichproben wächst.

model_l2 = LinearSVC(penalty="l2", loss="squared_hinge", dual=True)
Cs = np.logspace(-8, 4, 11)

labels = [f"fraction: {train_size}" for train_size in train_sizes]
results = {"C": Cs}
for label, train_size in zip(labels, train_sizes):
    cv = ShuffleSplit(train_size=train_size, **shuffle_params)
    train_scores, test_scores = validation_curve(
        model_l2,
        X,
        y,
        param_name="C",
        param_range=Cs,
        cv=cv,
        n_jobs=2,
    )
    results[label] = test_scores.mean(axis=1)
results = pd.DataFrame(results)

import matplotlib.pyplot as plt

fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(12, 6))

# plot results without scaling C
results.plot(x="C", ax=axes[0], logx=True)
axes[0].set_ylabel("CV score")
axes[0].set_title("No scaling")

for label in labels:
    best_C = results.loc[results[label].idxmax(), "C"]
    axes[0].axvline(x=best_C, linestyle="--", color="grey", alpha=0.8)

# plot results by scaling C
for train_size_idx, label in enumerate(labels):
    results_scaled = results[[label]].assign(
        C_scaled=Cs * float(n_samples * np.sqrt(train_sizes[train_size_idx]))
    )
    results_scaled.plot(x="C_scaled", ax=axes[1], logx=True, label=label)
    best_C_scaled = results_scaled["C_scaled"].loc[results[label].idxmax()]
    axes[1].axvline(x=best_C_scaled, linestyle="--", color="grey", alpha=0.8)
axes[1].set_title("Scaling C by sqrt(1 / n_samples)")

fig.suptitle("Effect of scaling C with L2 penalty")
plt.show()

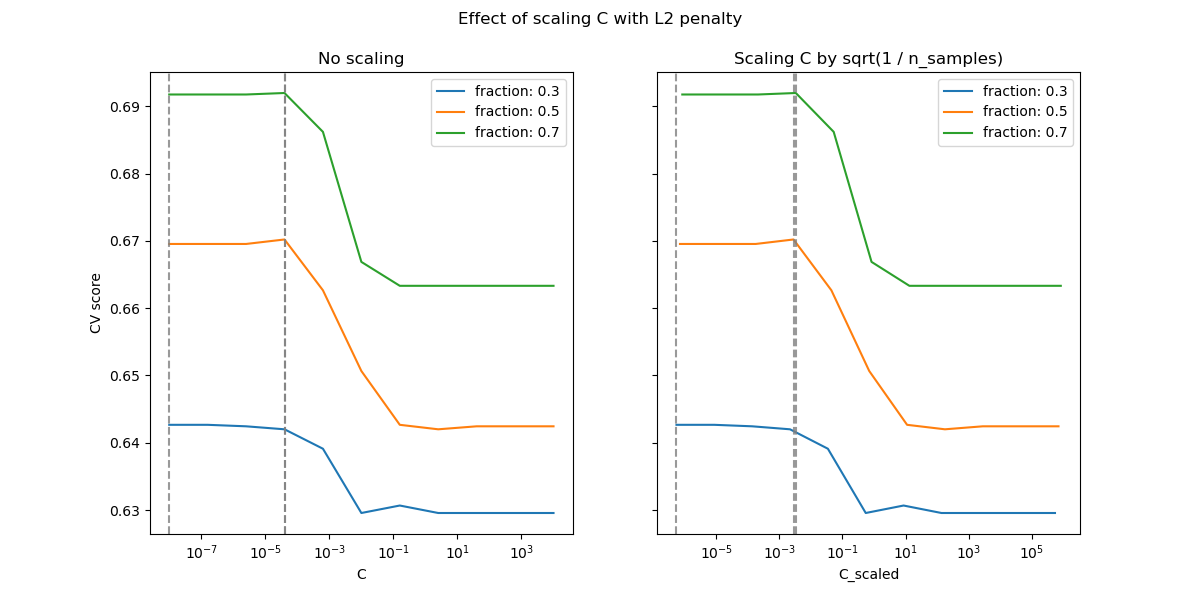
Für den L2-Strafen-Fall scheint die Neuparametrisierung einen geringeren Einfluss auf die Stabilität des optimalen Werts für die Regularisierung zu haben. Der Übergang aus der Overfitting-Region erfolgt in einem breiteren Bereich, und die Genauigkeit scheint bis zum Zufallsniveau nicht beeinträchtigt zu werden.

Versuchen Sie, den Wert auf n_splits=1_000 zu erhöhen, um bessere Ergebnisse im L2-Fall zu erzielen, was hier aufgrund von Einschränkungen des Dokumentations-Builders nicht gezeigt wird.

Verwandte Beispiele

L1-Strafe und Sparsity in Logistischer Regression

L1-Strafe und Sparsity in Logistischer Regression

Ridge-Koeffizienten als Funktion der L2-Regularisierung

Ridge-Koeffizienten als Funktion der L2-Regularisierung

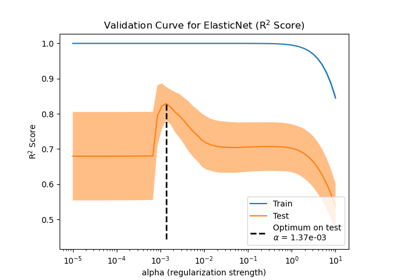
Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Auswirkung der Modellregularisierung auf Trainings- und Testfehler

Bedeutung der Merkmalskalierung

Bedeutung der Merkmalskalierung