Klassifizierungsgrenzen mit verschiedenen SVM-Kernen plotten

Dieses Beispiel zeigt, wie verschiedene Kernel in einem SVC (Support Vector Classifier) die Klassifizierungsgrenzen in einem binären, zweidimensionalen Klassifizierungsproblem beeinflussen.

SVCs zielen darauf ab, eine Hyperebene zu finden, die die Klassen in ihren Trainingsdaten effektiv trennt, indem sie den Abstand zwischen den äußersten Datenpunkten jeder Klasse maximiert. Dies wird erreicht, indem der beste Gewichtsvektor \(w\) gefunden wird, der die Entscheidungsgrenzen-Hyperebene definiert und die Summe der Hinge-Verluste für falsch klassifizierte Stichproben minimiert, gemessen anhand der hinge_loss Funktion. Standardmäßig wird die Regularisierung mit dem Parameter C=1 angewendet, was eine gewisse Toleranz für Fehlklassifizierungen zulässt.

Wenn die Daten im ursprünglichen Merkmalsraum nicht linear trennbar sind, kann ein nichtlinearer Kernel-Parameter gesetzt werden. Abhängig vom Kernel beinhaltet der Prozess das Hinzufügen neuer Merkmale oder das Transformieren bestehender Merkmale, um die Daten anzureichern und potenziell bedeutungsvoller zu machen. Wenn ein anderer Kernel als "linear" gesetzt ist, wendet der SVC den Kernel-Trick an, der die Ähnlichkeit zwischen Datenpunktpaaren mithilfe der Kernel-Funktion berechnet, ohne den gesamten Datensatz explizit zu transformieren. Der Kernel-Trick übertrifft die ansonsten notwendige Matrixtransformation des gesamten Datensatzes, indem er nur die Beziehungen zwischen allen Datenpunktpaaren berücksichtigt. Die Kernel-Funktion bildet zwei Vektoren (jedes Beobachtungspaar) auf ihre Ähnlichkeit mittels ihres Skalarprodukts ab.

Die Hyperebene kann dann mithilfe der Kernel-Funktion berechnet werden, als ob der Datensatz in einem höherdimensionalen Raum dargestellt wäre. Die Verwendung einer Kernel-Funktion anstelle einer expliziten Matrixtransformation verbessert die Leistung, da die Kernel-Funktion eine Zeitkomplexität von \(O({n}^2)\) hat, während die Matrixtransformation entsprechend der spezifischen angewendeten Transformation skaliert.

In diesem Beispiel vergleichen wir die gängigsten Kernel-Typen von Support Vector Machines: den linearen Kernel ("linear"), den polynomialen Kernel ("poly"), den Radial Basis Function (RBF)-Kernel ("rbf") und den Sigmoid-Kernel ("sigmoid").

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Erstellung eines Datensatzes

Wir erstellen einen zweidimensionalen Klassifizierungsdatensatz mit 16 Stichproben und zwei Klassen. Wir plotten die Stichproben mit Farben, die ihren jeweiligen Zielen entsprechen.

import matplotlib.pyplot as plt
import numpy as np

X = np.array(
    [
        [0.4, -0.7],
        [-1.5, -1.0],
        [-1.4, -0.9],
        [-1.3, -1.2],
        [-1.1, -0.2],
        [-1.2, -0.4],
        [-0.5, 1.2],
        [-1.5, 2.1],
        [1.0, 1.0],
        [1.3, 0.8],
        [1.2, 0.5],
        [0.2, -2.0],
        [0.5, -2.4],
        [0.2, -2.3],
        [0.0, -2.7],
        [1.3, 2.1],
    ]
)

y = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1])

# Plotting settings
fig, ax = plt.subplots(figsize=(4, 3))
x_min, x_max, y_min, y_max = -3, 3, -3, 3
ax.set(xlim=(x_min, x_max), ylim=(y_min, y_max))

# Plot samples by color and add legend
scatter = ax.scatter(X[:, 0], X[:, 1], s=150, c=y, label=y, edgecolors="k")
ax.legend(*scatter.legend_elements(), loc="upper right", title="Classes")
ax.set_title("Samples in two-dimensional feature space")
plt.show()

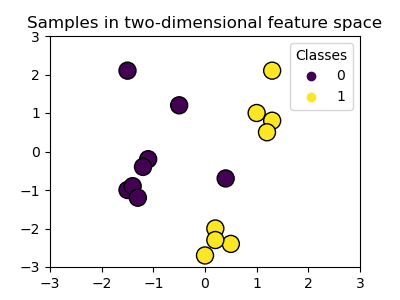
Wir sehen, dass die Stichproben durch eine gerade Linie nicht eindeutig trennbar sind.

Training eines SVC-Modells und Plotten von Entscheidungsgrenzen

Wir definieren eine Funktion, die einen SVC-Klassifikator anpasst, wobei der Parameter kernel als Eingabe zugelassen wird, und plottet dann die vom Modell gelernten Entscheidungsgrenzen mithilfe von DecisionBoundaryDisplay.

Beachten Sie, dass der Parameter C der Einfachheit halber auf seinen Standardwert (C=1) gesetzt ist und der Parameter gamma über alle Kernel hinweg auf gamma=2 gesetzt ist, obwohl er für den linearen Kernel automatisch ignoriert wird. In einer realen Klassifizierungsaufgabe, bei der die Leistung zählt, ist die Parameteroptimierung (z. B. mithilfe von GridSearchCV) sehr empfehlenswert, um verschiedene Strukturen innerhalb der Daten zu erfassen.

Das Setzen von response_method="predict" in DecisionBoundaryDisplay färbt die Bereiche basierend auf ihrer vorhergesagten Klasse. Die Verwendung von response_method="decision_function" ermöglicht es uns auch, die Entscheidungsgrenze und die Ränder zu beiden Seiten davon zu plotten. Schließlich werden die während des Trainings verwendeten Stützvektoren (die immer auf den Rändern liegen) mithilfe des Attributs support_vectors_ der trainierten SVCs identifiziert und ebenfalls geplottet.

from sklearn import svm
from sklearn.inspection import DecisionBoundaryDisplay


def plot_training_data_with_decision_boundary(
    kernel, ax=None, long_title=True, support_vectors=True
):
    # Train the SVC
    clf = svm.SVC(kernel=kernel, gamma=2).fit(X, y)

    # Settings for plotting
    if ax is None:
        _, ax = plt.subplots(figsize=(4, 3))
    x_min, x_max, y_min, y_max = -3, 3, -3, 3
    ax.set(xlim=(x_min, x_max), ylim=(y_min, y_max))

    # Plot decision boundary and margins
    common_params = {"estimator": clf, "X": X, "ax": ax}
    DecisionBoundaryDisplay.from_estimator(
        **common_params,
        response_method="predict",
        plot_method="pcolormesh",
        alpha=0.3,
    )
    DecisionBoundaryDisplay.from_estimator(
        **common_params,
        response_method="decision_function",
        plot_method="contour",
        levels=[-1, 0, 1],
        colors=["k", "k", "k"],
        linestyles=["--", "-", "--"],
    )

    if support_vectors:
        # Plot bigger circles around samples that serve as support vectors
        ax.scatter(
            clf.support_vectors_[:, 0],
            clf.support_vectors_[:, 1],
            s=150,
            facecolors="none",
            edgecolors="k",
        )

    # Plot samples by color and add legend
    ax.scatter(X[:, 0], X[:, 1], c=y, s=30, edgecolors="k")
    ax.legend(*scatter.legend_elements(), loc="upper right", title="Classes")
    if long_title:
        ax.set_title(f" Decision boundaries of {kernel} kernel in SVC")
    else:
        ax.set_title(kernel)

    if ax is None:
        plt.show()

Linearer Kernel

Der lineare Kernel ist das Skalarprodukt der Eingabestichproben

\[K(\mathbf{x}_1, \mathbf{x}_2) = \mathbf{x}_1^\top \mathbf{x}_2\]

Er wird dann auf jede Kombination von zwei Datenpunkten (Stichproben) im Datensatz angewendet. Das Skalarprodukt der beiden Punkte bestimmt die cosine_similarity zwischen beiden Punkten. Je höher der Wert, desto ähnlicher sind sich die Punkte.

plot_training_data_with_decision_boundary("linear")

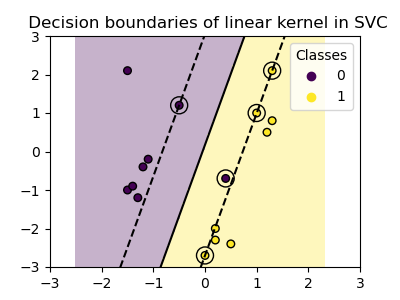
Das Training eines SVC mit einem linearen Kernel führt zu einem unveränderten Merkmalsraum, in dem die Hyperebene und die Ränder gerade Linien sind. Aufgrund der mangelnden Ausdruckskraft des linearen Kernels erfassen die trainierten Klassen die Trainingsdaten nicht perfekt.

Polynomieller Kernel

Der polynomiale Kernel verändert die Vorstellung von Ähnlichkeit. Die Kernel-Funktion ist definiert als

\[K(\mathbf{x}_1, \mathbf{x}_2) = (\gamma \cdot \ \mathbf{x}_1^\top\mathbf{x}_2 + r)^d\]

wobei \(d\) der Grad (degree) des Polynoms ist, \({\gamma}\) (gamma) den Einfluss jeder einzelnen Trainingsstichprobe auf die Entscheidungsgrenze steuert und \(r\) der Bias-Term (coef0) ist, der die Daten nach oben oder unten verschiebt. Hier verwenden wir den Standardwert für den Grad des Polynoms in der Kernel-Funktion (degree=3). Wenn coef0=0 (der Standardwert) ist, werden die Daten nur transformiert, aber keine zusätzliche Dimension hinzugefügt. Die Verwendung eines polynomialen Kernels ist äquivalent zur Erstellung von PolynomialFeatures und anschließendem Anpassen eines SVC mit einem linearen Kernel auf den transformierten Daten, obwohl dieser alternative Ansatz für die meisten Datensätze rechenintensiv wäre.

plot_training_data_with_decision_boundary("poly")

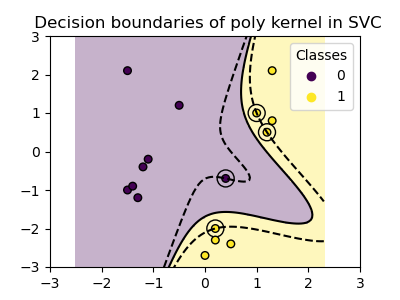
Der polynomiale Kernel mit gamma=2 passt sich gut an die Trainingsdaten an und bewirkt, dass sich die Ränder auf beiden Seiten der Hyperebene entsprechend krümmen.

RBF-Kernel

Der Radial Basis Function (RBF)-Kernel, auch bekannt als Gaußscher Kernel, ist der Standardkernel für Support Vector Machines in scikit-learn. Er misst die Ähnlichkeit zwischen zwei Datenpunkten in unendlich vielen Dimensionen und nähert dann die Klassifizierung durch Mehrheitsentscheid an. Die Kernel-Funktion ist definiert als

\[K(\mathbf{x}_1, \mathbf{x}_2) = \exp\left(-\gamma \cdot {\|\mathbf{x}_1 - \mathbf{x}_2\|^2}\right)\]

wobei \({\gamma}\) (gamma) den Einfluss jeder einzelnen Trainingsstichprobe auf die Entscheidungsgrenze steuert.

Je größer der euklidische Abstand zwischen zwei Punkten \(\|\mathbf{x}_1 - \mathbf{x}_2\|^2\), desto näher liegt die Kernel-Funktion bei Null. Das bedeutet, dass zwei Punkte, die weit voneinander entfernt sind, wahrscheinlich unähnlich sind.

plot_training_data_with_decision_boundary("rbf")

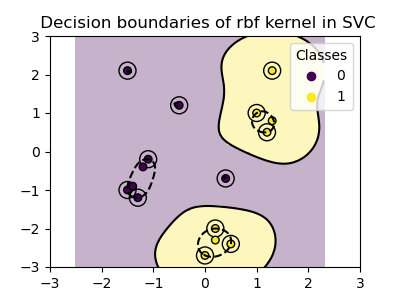
Im Plot sehen wir, wie sich die Entscheidungsgrenzen um Datenpunkte herum zusammenziehen, die nahe beieinander liegen.

Sigmoid-Kernel

Die Sigmoid-Kernel-Funktion ist definiert als

\[K(\mathbf{x}_1, \mathbf{x}_2) = \tanh(\gamma \cdot \mathbf{x}_1^\top\mathbf{x}_2 + r)\]

wobei der Kernel-Koeffizient \({\gamma}\) (gamma) den Einfluss jeder einzelnen Trainingsstichprobe auf die Entscheidungsgrenze steuert und \(r\) der Bias-Term (coef0) ist, der die Daten nach oben oder unten verschiebt.

Beim Sigmoid-Kernel wird die Ähnlichkeit zwischen zwei Datenpunkten mithilfe der hyperbolischen Tangensfunktion (\(\tanh\)) berechnet. Die Kernel-Funktion skaliert und verschiebt möglicherweise das Skalarprodukt der beiden Punkte (\(\mathbf{x}_1\) und \(\mathbf{x}_2\)).

plot_training_data_with_decision_boundary("sigmoid")

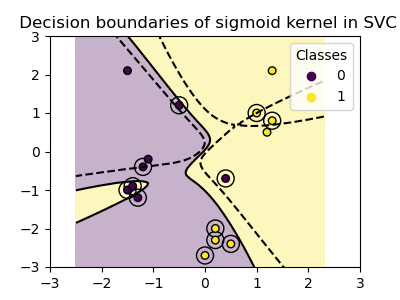
Wir sehen, dass die mit dem Sigmoid-Kernel erzielten Entscheidungsgrenzen gekrümmt und unregelmäßig erscheinen. Die Entscheidungsgrenze versucht, die Klassen zu trennen, indem sie eine sigmoidförmige Kurve anpasst, was zu einer komplexen Grenze führt, die möglicherweise nicht gut auf ungesehene Daten generalisiert. Aus diesem Beispiel wird deutlich, dass der Sigmoid-Kernel sehr spezifische Anwendungsfälle hat, wenn mit Daten gearbeitet wird, die eine sigmoide Form aufweisen. In diesem Beispiel könnte eine sorgfältige Feinabstimmung allgemeinere Entscheidungsgrenzen finden. Aufgrund seiner Spezifität wird der Sigmoid-Kernel in der Praxis seltener verwendet als andere Kernel.

Schlussfolgerung

In diesem Beispiel haben wir die mit dem bereitgestellten Datensatz trainierten Entscheidungsgrenzen visualisiert. Die Plots dienen als intuitive Demonstration, wie verschiedene Kernel die Trainingsdaten verwenden, um die Klassifizierungsgrenzen zu bestimmen.

Die Hyperebenen und Ränder, obwohl indirekt berechnet, können als Ebenen im transformierten Merkmalsraum vorgestellt werden. In den Plots werden sie jedoch relativ zum ursprünglichen Merkmalsraum dargestellt, was zu gekrümmten Entscheidungsgrenzen für die polynomialen, RBF- und Sigmoid-Kernel führt.

Bitte beachten Sie, dass die Plots nicht die Genauigkeit oder Qualität einzelner Kernel bewerten. Sie sollen ein visuelles Verständnis dafür vermitteln, wie die verschiedenen Kernel die Trainingsdaten verwenden.

Für eine umfassende Bewertung wird die Feinabstimmung der SVC-Parameter mithilfe von Techniken wie GridSearchCV empfohlen, um die zugrundeliegenden Strukturen innerhalb der Daten zu erfassen.

XOR-Datensatz

Ein klassisches Beispiel für einen Datensatz, der nicht linear trennbar ist, ist das XOR-Muster. Hier zeigen wir, wie verschiedene Kernel auf einem solchen Datensatz funktionieren.

xx, yy = np.meshgrid(np.linspace(-3, 3, 500), np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)

_, ax = plt.subplots(2, 2, figsize=(8, 8))
args = dict(long_title=False, support_vectors=False)
plot_training_data_with_decision_boundary("linear", ax[0, 0], **args)
plot_training_data_with_decision_boundary("poly", ax[0, 1], **args)
plot_training_data_with_decision_boundary("rbf", ax[1, 0], **args)
plot_training_data_with_decision_boundary("sigmoid", ax[1, 1], **args)
plt.show()

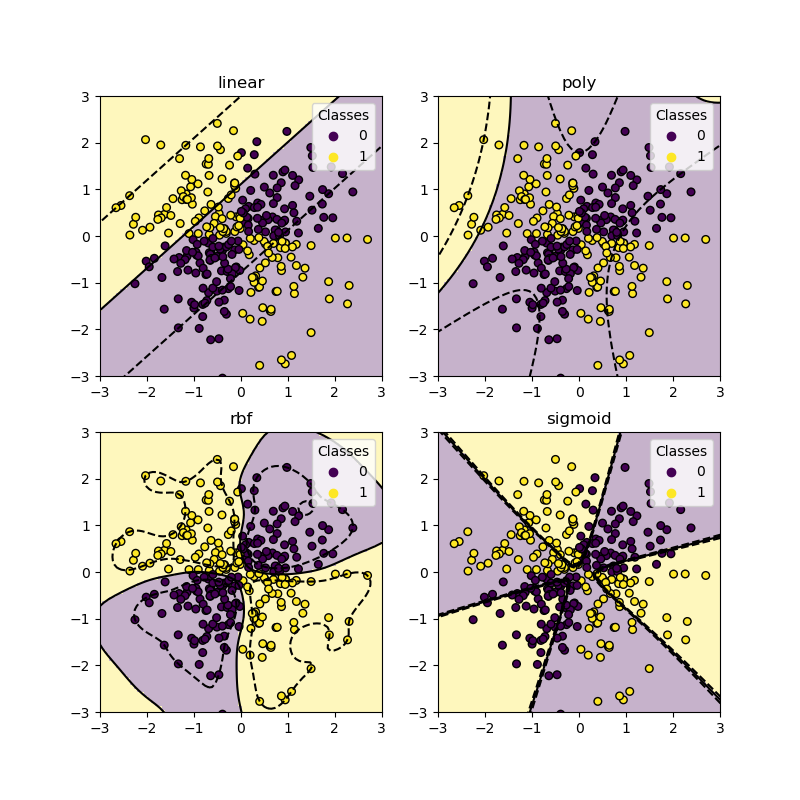
Wie Sie aus den obigen Plots ersehen können, kann nur der rbf-Kernel eine vernünftige Entscheidungsgrenze für den obigen Datensatz finden.

Verwandte Beispiele

RBF SVM Parameter

RBF SVM Parameter

Verschiedene SVM-Klassifikatoren im Iris-Datensatz plotten

Verschiedene SVM-Klassifikatoren im Iris-Datensatz plotten

SVM: Maximum Margin Trennhyperplane

SVM: Maximum Margin Trennhyperplane

SVM: Trennhyperplane für unausgeglichene Klassen

SVM: Trennhyperplane für unausgeglichene Klassen