Anpassung für Zufall bei der Bewertung der Clustering-Leistung

Dieses Notebook untersucht die Auswirkungen von gleichmäßig verteilten zufälligen Beschriftungen auf das Verhalten einiger Metriken zur Bewertung von Clustern. Zu diesem Zweck werden die Metriken mit einer festen Anzahl von Stichproben und in Abhängigkeit von der Anzahl der vom Schätzer zugewiesenen Cluster berechnet. Das Beispiel ist in zwei Experimente unterteilt:

• ein erstes Experiment mit festen „Ground Truth Labels“ (und damit fester Klassenzahl) und zufälligen „vorhergesagten Labels“;

• ein zweites Experiment mit variierenden „Ground Truth Labels“, zufälligen „vorhergesagten Labels“. Die „vorhergesagten Labels“ haben die gleiche Anzahl von Klassen und Clustern wie die „Ground Truth Labels“.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Definition der zu bewertenden Metrikenliste

Clustering-Algorithmen sind im Grunde unüberwachte Lernmethoden. Da wir in diesem Beispiel Klassenlabels für die synthetischen Cluster zuweisen, ist es möglich, Bewertungsmetriken zu verwenden, die diese „überwachten“ Ground-Truth-Informationen nutzen, um die Qualität der resultierenden Cluster zu quantifizieren. Beispiele für solche Metriken sind die folgenden:

• V-Maß, das harmonische Mittel aus Vollständigkeit und Homogenität;

• Rand-Index, der misst, wie häufig Paare von Datenpunkten gemäß dem Ergebnis des Clustering-Algorithmus und der Ground-Truth-Klassenzuweisung konsistent gruppiert werden;

• Angepasster Rand-Index (ARI), ein zufallsbereinigter Rand-Index, so dass eine zufällige Clusterzuweisung im Erwartungswert einen ARI von 0,0 hat;

• Mutual Information (MI) ist ein informationstheoretisches Maß, das quantifiziert, wie abhängig die beiden Labelings sind. Beachten Sie, dass der Maximalwert von MI für perfekte Labelings von der Anzahl der Cluster und der Stichproben abhängt;

• Normalisierte Mutual Information (NMI), eine Mutual Information, die zwischen 0 (keine Mutual Information) im Grenzwert großer Datenpunktmengen und 1 (perfekt übereinstimmende Labelzuweisungen, bis auf eine Permutation der Labels) definiert ist. Sie ist nicht zufallsbereinigt: Wenn die Anzahl der geclusterten Datenpunkte nicht groß genug ist, können die Erwartungswerte von MI oder NMI für zufällige Labelings signifikant von Null abweichen;

• Angepasste Mutual Information (AMI), eine zufallsbereinigte Mutual Information. Ähnlich wie bei ARI hat eine zufällige Clusterzuweisung im Erwartungswert einen AMI von 0,0.

Weitere Informationen finden Sie im Modul Bewertung der Clustering-Leistung.

from sklearn import metrics

score_funcs = [
    ("V-measure", metrics.v_measure_score),
    ("Rand index", metrics.rand_score),
    ("ARI", metrics.adjusted_rand_score),
    ("MI", metrics.mutual_info_score),
    ("NMI", metrics.normalized_mutual_info_score),
    ("AMI", metrics.adjusted_mutual_info_score),
]

Erstes Experiment: feste Ground Truth Labels und wachsende Anzahl von Clustern

Zuerst definieren wir eine Funktion, die gleichmäßig verteilte zufällige Beschriftungen erstellt.

import numpy as np

rng = np.random.RandomState(0)


def random_labels(n_samples, n_classes):
    return rng.randint(low=0, high=n_classes, size=n_samples)

Eine weitere Funktion verwendet die Funktion random_labels, um einen festen Satz von Ground Truth Labels (labels_a) zu erstellen, die in n_classes verteilt sind, und bewertet dann mehrere Sätze von zufälligen „vorhergesagten“ Labels (labels_b), um die Variabilität einer gegebenen Metrik bei einer gegebenen n_clusters zu beurteilen.

def fixed_classes_uniform_labelings_scores(
    score_func, n_samples, n_clusters_range, n_classes, n_runs=5
):
    scores = np.zeros((len(n_clusters_range), n_runs))
    labels_a = random_labels(n_samples=n_samples, n_classes=n_classes)

    for i, n_clusters in enumerate(n_clusters_range):
        for j in range(n_runs):
            labels_b = random_labels(n_samples=n_samples, n_classes=n_clusters)
            scores[i, j] = score_func(labels_a, labels_b)
    return scores

In diesem ersten Beispiel setzen wir die Anzahl der Klassen (wahre Anzahl von Clustern) auf n_classes=10. Die Anzahl der Cluster variiert über die von n_clusters_range bereitgestellten Werte.

import matplotlib.pyplot as plt
import seaborn as sns

n_samples = 1000
n_classes = 10
n_clusters_range = np.linspace(2, 100, 10).astype(int)
plots = []
names = []

sns.color_palette("colorblind")
plt.figure(1)

for marker, (score_name, score_func) in zip("d^vx.,", score_funcs):
    scores = fixed_classes_uniform_labelings_scores(
        score_func, n_samples, n_clusters_range, n_classes=n_classes
    )
    plots.append(
        plt.errorbar(
            n_clusters_range,
            scores.mean(axis=1),
            scores.std(axis=1),
            alpha=0.8,
            linewidth=1,
            marker=marker,
        )[0]
    )
    names.append(score_name)

plt.title(
    "Clustering measures for random uniform labeling\n"
    f"against reference assignment with {n_classes} classes"
)
plt.xlabel(f"Number of clusters (Number of samples is fixed to {n_samples})")
plt.ylabel("Score value")
plt.ylim(bottom=-0.05, top=1.05)
plt.legend(plots, names, bbox_to_anchor=(0.5, 0.5))
plt.show()

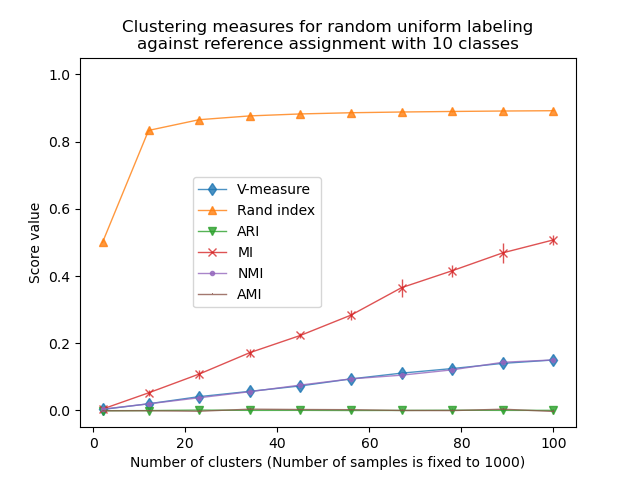
Der Rand-Index sättigt für n_clusters > n_classes. Andere nicht-angepasste Metriken wie das V-Maß zeigen eine lineare Abhängigkeit zwischen der Anzahl der Cluster und der Anzahl der Stichproben.

Zufallsbereinigte Metriken wie ARI und AMI zeigen einige zufällige Variationen, die um einen mittleren Score von 0,0 zentriert sind, unabhängig von der Anzahl der Stichproben und Cluster.

Zweites Experiment: variierende Anzahl von Klassen und Clustern

In diesem Abschnitt definieren wir eine ähnliche Funktion, die mehrere Metriken verwendet, um 2 gleichmäßig verteilte zufällige Labelings zu bewerten. In diesem Fall werden die Anzahl der Klassen und die zugewiesene Anzahl von Clustern für jeden möglichen Wert im Bereich von n_clusters_range aufeinander abgestimmt.

def uniform_labelings_scores(score_func, n_samples, n_clusters_range, n_runs=5):
    scores = np.zeros((len(n_clusters_range), n_runs))

    for i, n_clusters in enumerate(n_clusters_range):
        for j in range(n_runs):
            labels_a = random_labels(n_samples=n_samples, n_classes=n_clusters)
            labels_b = random_labels(n_samples=n_samples, n_classes=n_clusters)
            scores[i, j] = score_func(labels_a, labels_b)
    return scores

In diesem Fall verwenden wir n_samples=100, um die Auswirkung einer Clusteranzahl zu zeigen, die der Anzahl der Stichproben nahe kommt oder gleich ist.

n_samples = 100
n_clusters_range = np.linspace(2, n_samples, 10).astype(int)

plt.figure(2)

plots = []
names = []

for marker, (score_name, score_func) in zip("d^vx.,", score_funcs):
    scores = uniform_labelings_scores(score_func, n_samples, n_clusters_range)
    plots.append(
        plt.errorbar(
            n_clusters_range,
            np.median(scores, axis=1),
            scores.std(axis=1),
            alpha=0.8,
            linewidth=2,
            marker=marker,
        )[0]
    )
    names.append(score_name)

plt.title(
    "Clustering measures for 2 random uniform labelings\nwith equal number of clusters"
)
plt.xlabel(f"Number of clusters (Number of samples is fixed to {n_samples})")
plt.ylabel("Score value")
plt.legend(plots, names)
plt.ylim(bottom=-0.05, top=1.05)
plt.show()

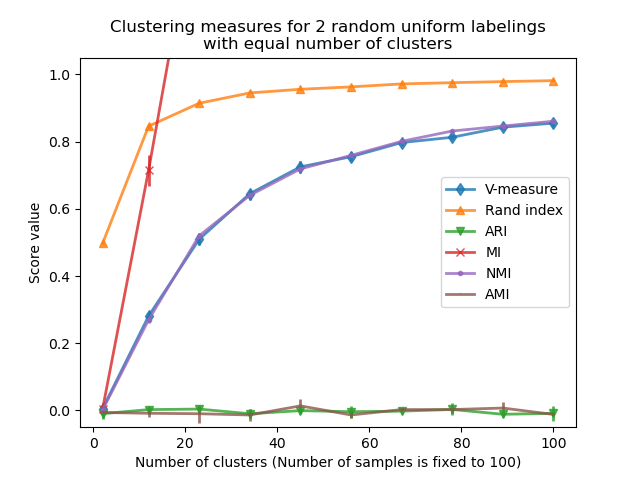
Wir beobachten ähnliche Ergebnisse wie im ersten Experiment: zufallsbereinigte Metriken bleiben konstant nahe Null, während andere Metriken tendenziell mit feingranularen Labelings größer werden. Das mittlere V-Maß von zufälligen Labelings steigt signifikant an, je näher die Anzahl der Cluster der Gesamtzahl der zur Berechnung der Metrik verwendeten Stichproben ist. Darüber hinaus ist die rohe Mutual Information nach oben unbegrenzt und ihre Skalierung hängt von den Dimensionen des Clustering-Problems und der Kardinalität der Ground Truth Klassen ab. Deshalb geht die Kurve aus dem Diagramm.

Nur angepasste Metriken können daher sicher als Konsensindex verwendet werden, um die durchschnittliche Stabilität von Clustering-Algorithmen für einen gegebenen Wert von k auf verschiedenen überlappenden Teilmengen des Datensatzes zu bewerten.

Nicht-angepasste Metriken zur Bewertung von Clustern können daher irreführend sein, da sie große Werte für feingranulare Labelings ausgeben. Man könnte denken, dass das Labeling aussagekräftige Gruppen erfasst hat, obwohl sie völlig zufällig sein können. Insbesondere solche nicht-angepassten Metriken sollten nicht verwendet werden, um die Ergebnisse verschiedener Clustering-Algorithmen zu vergleichen, die eine unterschiedliche Anzahl von Clustern ausgeben.

Verwandte Beispiele

Demo des DBSCAN Clustering Algorithmus

Demo des DBSCAN Clustering Algorithmus

Clustering von Textdokumenten mit K-Means

Clustering von Textdokumenten mit K-Means

Auswahl der Anzahl von Clustern mit Silhouette-Analyse auf KMeans-Clustering

Auswahl der Anzahl von Clustern mit Silhouette-Analyse auf KMeans-Clustering

Agglomeratives Clustering mit verschiedenen Metriken

Agglomeratives Clustering mit verschiedenen Metriken