Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Modellbasierte und sequentielle Merkmalsauswahl#
Dieses Beispiel veranschaulicht und vergleicht zwei Ansätze zur Merkmalsauswahl: SelectFromModel, das auf Merkmalsbedeutung basiert, und SequentialFeatureSelector, das einen gierigen Ansatz verfolgt.
Wir verwenden den Diabetes-Datensatz, der 10 Merkmale von 442 Diabetespatienten enthält.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Daten laden#
Wir laden zunächst den Diabetes-Datensatz, der innerhalb von scikit-learn verfügbar ist, und geben seine Beschreibung aus
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target
print(diabetes.DESCR)
.. _diabetes_dataset:
Diabetes dataset
----------------
Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.
**Data Set Characteristics:**
:Number of Instances: 442
:Number of Attributes: First 10 columns are numeric predictive values
:Target: Column 11 is a quantitative measure of disease progression one year after baseline
:Attribute Information:
- age age in years
- sex
- bmi body mass index
- bp average blood pressure
- s1 tc, total serum cholesterol
- s2 ldl, low-density lipoproteins
- s3 hdl, high-density lipoproteins
- s4 tch, total cholesterol / HDL
- s5 ltg, possibly log of serum triglycerides level
- s6 glu, blood sugar level
Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times the square root of `n_samples` (i.e. the sum of squares of each column totals 1).
Source URL:
https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html
For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)
Merkmalsbedeutung aus Koeffizienten#
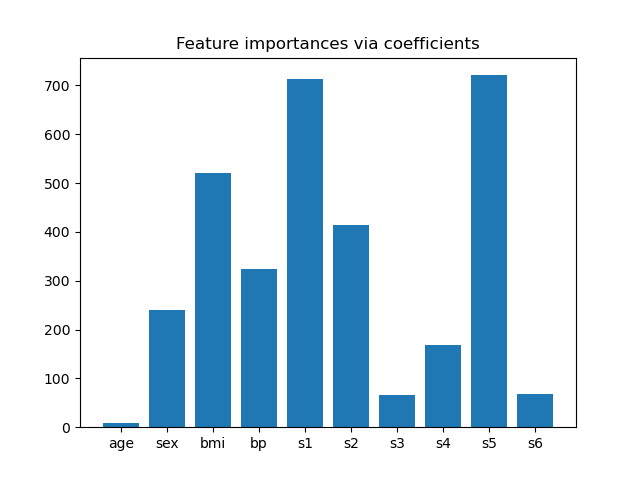
Um eine Vorstellung von der Bedeutung der Merkmale zu bekommen, werden wir den RidgeCV-Estimator verwenden. Die Merkmale mit dem höchsten absoluten coef_-Wert gelten als die wichtigsten. Wir können die Koeffizienten direkt beobachten, ohne sie skalieren zu müssen (oder die Daten zu skalieren), da wir aus der obigen Beschreibung wissen, dass die Merkmale bereits standardisiert wurden. Für ein vollständigeres Beispiel zur Interpretation der Koeffizienten linearer Modelle siehe Häufige Fallstricke bei der Interpretation von Koeffizienten linearer Modelle.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import RidgeCV
ridge = RidgeCV(alphas=np.logspace(-6, 6, num=5)).fit(X, y)
importance = np.abs(ridge.coef_)
feature_names = np.array(diabetes.feature_names)
plt.bar(height=importance, x=feature_names)
plt.title("Feature importances via coefficients")
plt.show()
Merkmale basierend auf Bedeutung auswählen#
Nun wollen wir die beiden wichtigsten Merkmale gemäß den Koeffizienten auswählen. SelectFromModel ist genau dafür gedacht. SelectFromModel akzeptiert einen threshold-Parameter und wählt die Merkmale aus, deren Bedeutung (definiert durch die Koeffizienten) über diesem Schwellenwert liegt.
Da wir nur 2 Merkmale auswählen wollen, setzen wir diesen Schwellenwert knapp über dem Koeffizienten des drittwichtigsten Merkmals.
from time import time
from sklearn.feature_selection import SelectFromModel
threshold = np.sort(importance)[-3] + 0.01
tic = time()
sfm = SelectFromModel(ridge, threshold=threshold).fit(X, y)
toc = time()
print(f"Features selected by SelectFromModel: {feature_names[sfm.get_support()]}")
print(f"Done in {toc - tic:.3f}s")
Features selected by SelectFromModel: ['s1' 's5']
Done in 0.002s
Merkmale mit sequentieller Merkmalsauswahl auswählen#
Eine weitere Möglichkeit zur Merkmalsauswahl ist die Verwendung von SequentialFeatureSelector (SFS). SFS ist ein gieriges Verfahren, bei dem wir in jeder Iteration das beste neue Merkmal auswählen, das wir unseren ausgewählten Merkmalen basierend auf einem Kreuzvalidierungsergebnis hinzufügen. Das heißt, wir beginnen mit 0 Merkmalen und wählen das beste einzelne Merkmal mit der höchsten Punktzahl aus. Das Verfahren wird wiederholt, bis wir die gewünschte Anzahl ausgewählter Merkmale erreichen.
Wir können auch in umgekehrter Richtung vorgehen (backward SFS), d. h. wir beginnen mit allen Merkmalen und wählen gierig Merkmale aus, die nacheinander entfernt werden sollen. Wir veranschaulichen hier beide Ansätze.
from sklearn.feature_selection import SequentialFeatureSelector
tic_fwd = time()
sfs_forward = SequentialFeatureSelector(
ridge, n_features_to_select=2, direction="forward"
).fit(X, y)
toc_fwd = time()
tic_bwd = time()
sfs_backward = SequentialFeatureSelector(
ridge, n_features_to_select=2, direction="backward"
).fit(X, y)
toc_bwd = time()
print(
"Features selected by forward sequential selection: "
f"{feature_names[sfs_forward.get_support()]}"
)
print(f"Done in {toc_fwd - tic_fwd:.3f}s")
print(
"Features selected by backward sequential selection: "
f"{feature_names[sfs_backward.get_support()]}"
)
print(f"Done in {toc_bwd - tic_bwd:.3f}s")
Features selected by forward sequential selection: ['bmi' 's5']
Done in 0.178s
Features selected by backward sequential selection: ['bmi' 's5']
Done in 0.515s
Interessanterweise haben die Vorwärts- und Rückwärtsauswahl die gleiche Merkmalsmenge ausgewählt. Im Allgemeinen ist dies nicht der Fall und die beiden Methoden würden zu unterschiedlichen Ergebnissen führen.
Wir stellen auch fest, dass die von SFS ausgewählten Merkmale von denen abweichen, die durch Merkmalsbedeutung ausgewählt wurden: SFS wählt bmi anstelle von s1. Dies erscheint jedoch vernünftig, da bmi dem drittwichtigsten Merkmal gemäß den Koeffizienten entspricht. Dies ist bemerkenswert, da SFS die Koeffizienten überhaupt nicht verwendet.
Abschließend ist festzustellen, dass SelectFromModel deutlich schneller ist als SFS. Tatsächlich muss SelectFromModel nur ein einziges Modell fitten, während SFS für jede der Iterationen viele verschiedene Modelle kreuzvalidieren muss. SFS arbeitet jedoch mit jedem Modell, während SelectFromModel erfordert, dass der zugrunde liegende Schätzer ein coef_-Attribut oder ein feature_importances_-Attribut bereitstellt. Die Vorwärts-SFS ist schneller als die Rückwärts-SFS, da sie nur n_features_to_select = 2 Iterationen durchführen muss, während die Rückwärts-SFS n_features - n_features_to_select = 8 Iterationen durchführen muss.
Verwendung negativer Toleranzwerte#
SequentialFeatureSelector kann verwendet werden, um Merkmale aus dem Datensatz zu entfernen und eine kleinere Teilmenge der ursprünglichen Merkmale mit direction="backward" und einem negativen Wert von tol zurückzugeben.
Wir beginnen mit dem Laden des Brustkrebs-Datensatzes, der aus 30 verschiedenen Merkmalen und 569 Stichproben besteht.
import numpy as np
from sklearn.datasets import load_breast_cancer
breast_cancer_data = load_breast_cancer()
X, y = breast_cancer_data.data, breast_cancer_data.target
feature_names = np.array(breast_cancer_data.feature_names)
print(breast_cancer_data.DESCR)
.. _breast_cancer_dataset:
Breast cancer Wisconsin (diagnostic) dataset
--------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 569
:Number of Attributes: 30 numeric, predictive attributes and the class
:Attribute Information:
- radius (mean of distances from center to points on the perimeter)
- texture (standard deviation of gray-scale values)
- perimeter
- area
- smoothness (local variation in radius lengths)
- compactness (perimeter^2 / area - 1.0)
- concavity (severity of concave portions of the contour)
- concave points (number of concave portions of the contour)
- symmetry
- fractal dimension ("coastline approximation" - 1)
The mean, standard error, and "worst" or largest (mean of the three
worst/largest values) of these features were computed for each image,
resulting in 30 features. For instance, field 0 is Mean Radius, field
10 is Radius SE, field 20 is Worst Radius.
- class:
- WDBC-Malignant
- WDBC-Benign
:Summary Statistics:
===================================== ====== ======
Min Max
===================================== ====== ======
radius (mean): 6.981 28.11
texture (mean): 9.71 39.28
perimeter (mean): 43.79 188.5
area (mean): 143.5 2501.0
smoothness (mean): 0.053 0.163
compactness (mean): 0.019 0.345
concavity (mean): 0.0 0.427
concave points (mean): 0.0 0.201
symmetry (mean): 0.106 0.304
fractal dimension (mean): 0.05 0.097
radius (standard error): 0.112 2.873
texture (standard error): 0.36 4.885
perimeter (standard error): 0.757 21.98
area (standard error): 6.802 542.2
smoothness (standard error): 0.002 0.031
compactness (standard error): 0.002 0.135
concavity (standard error): 0.0 0.396
concave points (standard error): 0.0 0.053
symmetry (standard error): 0.008 0.079
fractal dimension (standard error): 0.001 0.03
radius (worst): 7.93 36.04
texture (worst): 12.02 49.54
perimeter (worst): 50.41 251.2
area (worst): 185.2 4254.0
smoothness (worst): 0.071 0.223
compactness (worst): 0.027 1.058
concavity (worst): 0.0 1.252
concave points (worst): 0.0 0.291
symmetry (worst): 0.156 0.664
fractal dimension (worst): 0.055 0.208
===================================== ====== ======
:Missing Attribute Values: None
:Class Distribution: 212 - Malignant, 357 - Benign
:Creator: Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian
:Donor: Nick Street
:Date: November, 1995
This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.
https://goo.gl/U2Uwz2
Features are computed from a digitized image of a fine needle
aspirate (FNA) of a breast mass. They describe
characteristics of the cell nuclei present in the image.
Separating plane described above was obtained using
Multisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree
Construction Via Linear Programming." Proceedings of the 4th
Midwest Artificial Intelligence and Cognitive Science Society,
pp. 97-101, 1992], a classification method which uses linear
programming to construct a decision tree. Relevant features
were selected using an exhaustive search in the space of 1-4
features and 1-3 separating planes.
The actual linear program used to obtain the separating plane
in the 3-dimensional space is that described in:
[K. P. Bennett and O. L. Mangasarian: "Robust Linear
Programming Discrimination of Two Linearly Inseparable Sets",
Optimization Methods and Software 1, 1992, 23-34].
This database is also available through the UW CS ftp server:
ftp ftp.cs.wisc.edu
cd math-prog/cpo-dataset/machine-learn/WDBC/
.. dropdown:: References
- W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction
for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on
Electronic Imaging: Science and Technology, volume 1905, pages 861-870,
San Jose, CA, 1993.
- O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and
prognosis via linear programming. Operations Research, 43(4), pages 570-577,
July-August 1995.
- W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques
to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994)
163-171.
Wir werden den LogisticRegression-Estimator mit SequentialFeatureSelector zur Merkmalsauswahl verwenden.
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
for tol in [-1e-2, -1e-3, -1e-4]:
start = time()
feature_selector = SequentialFeatureSelector(
LogisticRegression(),
n_features_to_select="auto",
direction="backward",
scoring="roc_auc",
tol=tol,
n_jobs=2,
)
model = make_pipeline(StandardScaler(), feature_selector, LogisticRegression())
model.fit(X, y)
end = time()
print(f"\ntol: {tol}")
print(f"Features selected: {feature_names[model[1].get_support()]}")
print(f"ROC AUC score: {roc_auc_score(y, model.predict_proba(X)[:, 1]):.3f}")
print(f"Done in {end - start:.3f}s")
tol: -0.01
Features selected: ['worst perimeter']
ROC AUC score: 0.975
Done in 17.444s
tol: -0.001
Features selected: ['radius error' 'fractal dimension error' 'worst texture'
'worst perimeter' 'worst concave points']
ROC AUC score: 0.997
Done in 17.263s
tol: -0.0001
Features selected: ['mean compactness' 'mean concavity' 'mean concave points' 'radius error'
'area error' 'concave points error' 'symmetry error'
'fractal dimension error' 'worst texture' 'worst perimeter' 'worst area'
'worst concave points' 'worst symmetry']
ROC AUC score: 0.998
Done in 15.368s
Wir sehen, dass die Anzahl der ausgewählten Merkmale tendenziell zunimmt, wenn sich negative Werte von tol Null annähern. Die für die Merkmalsauswahl benötigte Zeit nimmt ebenfalls ab, wenn sich die Werte von tol Null nähern.
Gesamtlaufzeit des Skripts: (0 Minuten 50,848 Sekunden)
Verwandte Beispiele
Post-hoc-Anpassung des Cut-off-Punkts der Entscheidungskfunktion
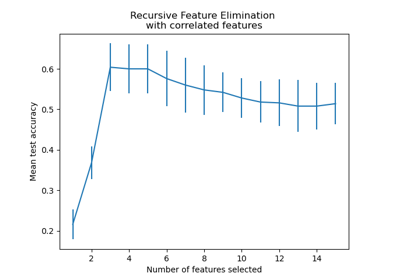
Rekursive Merkmalseliminierung mit Kreuzvalidierung