Empirische Evaluierung des Einflusses der k-means-Initialisierung

Bewerten Sie die Fähigkeit von k-means-Initialisierungsstrategien, die Konvergenz des Algorithmus robust zu machen, gemessen an der relativen Standardabweichung der Trägheit der Clusterbildung (d.h. der Summe der quadrierten Abstände zum nächsten Clusterzentrum).

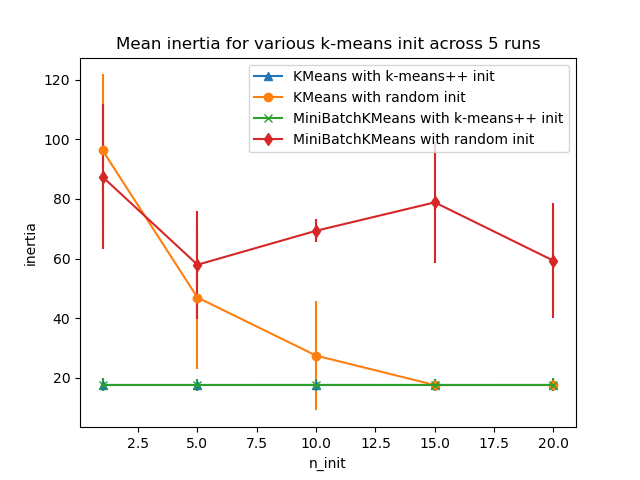
Das erste Diagramm zeigt die beste Trägheit, die für jede Kombination des Modells (KMeans oder MiniBatchKMeans) und der Init-Methode (init="random" oder init="k-means++") für steigende Werte des Parameters n_init, der die Anzahl der Initialisierungen steuert, erreicht wird.

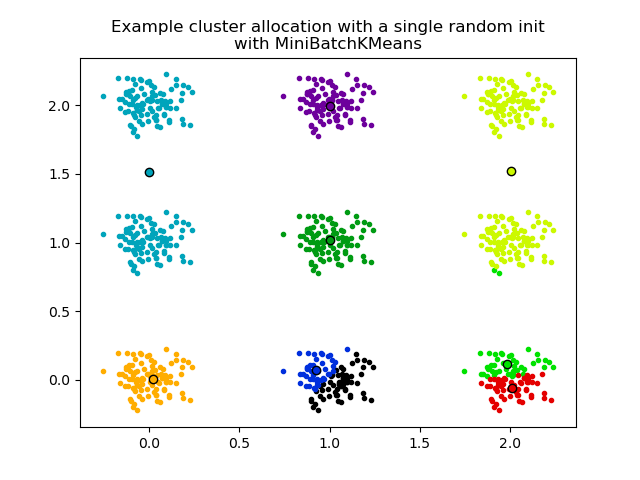
Das zweite Diagramm demonstriert einen einzigen Durchlauf des MiniBatchKMeans-Schätzers mit init="random" und n_init=1. Dieser Durchlauf führt zu einer schlechten Konvergenz (lokales Optimum), wobei die geschätzten Zentren zwischen den tatsächlichen Clustern feststecken.

Der für die Evaluierung verwendete Datensatz ist ein 2D-Gitter von weit verteilten isotropen Gaußschen Clustern.

• 
• 

Evaluation of KMeans with k-means++ init
Evaluation of KMeans with random init
Evaluation of MiniBatchKMeans with k-means++ init
Evaluation of MiniBatchKMeans with random init

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import KMeans, MiniBatchKMeans
from sklearn.utils import check_random_state, shuffle

random_state = np.random.RandomState(0)

# Number of run (with randomly generated dataset) for each strategy so as
# to be able to compute an estimate of the standard deviation
n_runs = 5

# k-means models can do several random inits so as to be able to trade
# CPU time for convergence robustness
n_init_range = np.array([1, 5, 10, 15, 20])

# Datasets generation parameters
n_samples_per_center = 100
grid_size = 3
scale = 0.1
n_clusters = grid_size**2


def make_data(random_state, n_samples_per_center, grid_size, scale):
    random_state = check_random_state(random_state)
    centers = np.array([[i, j] for i in range(grid_size) for j in range(grid_size)])
    n_clusters_true, n_features = centers.shape

    noise = random_state.normal(
        scale=scale, size=(n_samples_per_center, centers.shape[1])
    )

    X = np.concatenate([c + noise for c in centers])
    y = np.concatenate([[i] * n_samples_per_center for i in range(n_clusters_true)])
    return shuffle(X, y, random_state=random_state)


# Part 1: Quantitative evaluation of various init methods


plt.figure()
plots = []
legends = []

cases = [
    (KMeans, "k-means++", {}, "^-"),
    (KMeans, "random", {}, "o-"),
    (MiniBatchKMeans, "k-means++", {"max_no_improvement": 3}, "x-"),
    (MiniBatchKMeans, "random", {"max_no_improvement": 3, "init_size": 500}, "d-"),
]

for factory, init, params, format in cases:
    print("Evaluation of %s with %s init" % (factory.__name__, init))
    inertia = np.empty((len(n_init_range), n_runs))

    for run_id in range(n_runs):
        X, y = make_data(run_id, n_samples_per_center, grid_size, scale)
        for i, n_init in enumerate(n_init_range):
            km = factory(
                n_clusters=n_clusters,
                init=init,
                random_state=run_id,
                n_init=n_init,
                **params,
            ).fit(X)
            inertia[i, run_id] = km.inertia_
    p = plt.errorbar(
        n_init_range, inertia.mean(axis=1), inertia.std(axis=1), fmt=format
    )
    plots.append(p[0])
    legends.append("%s with %s init" % (factory.__name__, init))

plt.xlabel("n_init")
plt.ylabel("inertia")
plt.legend(plots, legends)
plt.title("Mean inertia for various k-means init across %d runs" % n_runs)

# Part 2: Qualitative visual inspection of the convergence

X, y = make_data(random_state, n_samples_per_center, grid_size, scale)
km = MiniBatchKMeans(
    n_clusters=n_clusters, init="random", n_init=1, random_state=random_state
).fit(X)

plt.figure()
for k in range(n_clusters):
    my_members = km.labels_ == k
    color = cm.nipy_spectral(float(k) / n_clusters, 1)
    plt.plot(X[my_members, 0], X[my_members, 1], ".", c=color)
    cluster_center = km.cluster_centers_[k]
    plt.plot(
        cluster_center[0],
        cluster_center[1],
        "o",
        markerfacecolor=color,
        markeredgecolor="k",
        markersize=6,
    )
    plt.title(
        "Example cluster allocation with a single random init\nwith MiniBatchKMeans"
    )

plt.show()

Verwandte Beispiele

Vergleich der K-Means und MiniBatchKMeans Clustering-Algorithmen

Vergleich der K-Means und MiniBatchKMeans Clustering-Algorithmen

Vergleich der Leistung von Bisecting K-Means und Regular K-Means

Vergleich der Leistung von Bisecting K-Means und Regular K-Means

Eine Demo des K-Means Clusterings auf den handschriftlichen Zifferndaten

Eine Demo des K-Means Clusterings auf den handschriftlichen Zifferndaten

Clustering von Textdokumenten mit K-Means

Clustering von Textdokumenten mit K-Means