Gaußsche Prozesse Regression: einfaches Einführungsexempel

Ein einfaches eindimensionales Regressionsbeispiel, das auf zwei verschiedene Arten berechnet wird

1. Ein rauschfreier Fall

2. Ein verrauschter Fall mit bekanntem Rauschpegel pro Datenpunkt

In beiden Fällen werden die Parameter des Kernels nach dem Maximum-Likelihood-Prinzip geschätzt.

Die Abbildungen veranschaulichen die interpolierende Eigenschaft des Gaußschen Prozessmodells sowie seine probabilistische Natur in Form eines punktweisen 95%-Konfidenzintervalls.

Beachten Sie, dass alpha ein Parameter ist, der die Stärke der Tichonoff-Regularisierung der angenommenen Kovarianzmatrix der Trainingspunkte steuert.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Datensatzgenerierung

Wir beginnen mit der Generierung eines synthetischen Datensatzes. Der wahre generative Prozess ist definiert als \(f(x) = x \sin(x)\).

import numpy as np

X = np.linspace(start=0, stop=10, num=1_000).reshape(-1, 1)
y = np.squeeze(X * np.sin(X))

import matplotlib.pyplot as plt

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("True generative process")

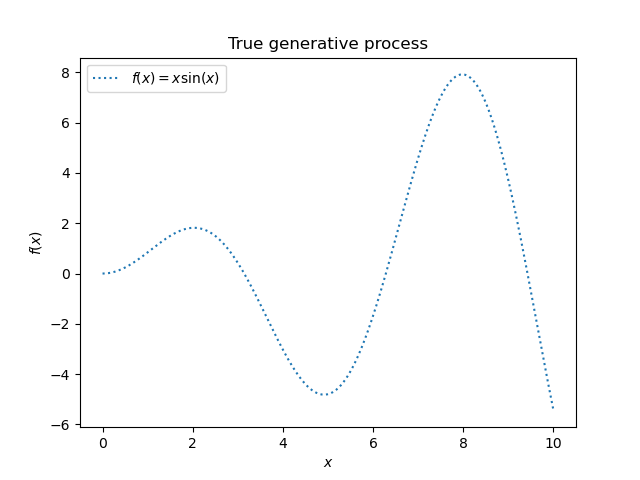
Wir werden diesen Datensatz im nächsten Experiment verwenden, um zu veranschaulichen, wie die Gaußsche Prozessregression funktioniert.

Beispiel mit rauschfreien Zielwerten

In diesem ersten Beispiel verwenden wir den wahren generativen Prozess, ohne zusätzliches Rauschen hinzuzufügen. Für das Training der Gaußschen Prozessregression wählen wir nur wenige Stichproben aus.

rng = np.random.RandomState(1)
training_indices = rng.choice(np.arange(y.size), size=6, replace=False)
X_train, y_train = X[training_indices], y[training_indices]

Nun passen wir einen Gaußschen Prozess an diese wenigen Trainingsdatenstichproben an. Wir verwenden einen Kernel vom Typ Radial Basis Function (RBF) und einen konstanten Parameter, um die Amplitude anzupassen.

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

kernel = 1 * RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e2))
gaussian_process = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)
gaussian_process.fit(X_train, y_train)
gaussian_process.kernel_

5.02**2 * RBF(length_scale=1.43)

Nach dem Anpassen unseres Modells sehen wir, dass die Hyperparameter des Kernels optimiert wurden. Nun verwenden wir unseren Kernel, um die mittlere Vorhersage für den gesamten Datensatz zu berechnen und das 95%-Konfidenzintervall zu plotten.

mean_prediction, std_prediction = gaussian_process.predict(X, return_std=True)

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.scatter(X_train, y_train, label="Observations")
plt.plot(X, mean_prediction, label="Mean prediction")
plt.fill_between(
    X.ravel(),
    mean_prediction - 1.96 * std_prediction,
    mean_prediction + 1.96 * std_prediction,
    alpha=0.5,
    label=r"95% confidence interval",
)
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("Gaussian process regression on noise-free dataset")

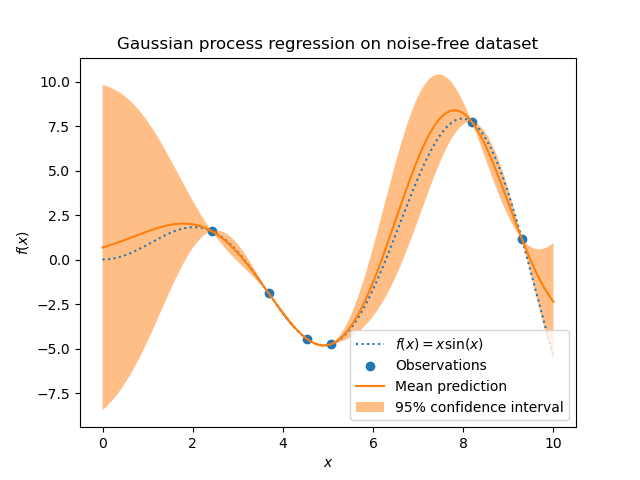
Wir sehen, dass für eine Vorhersage für einen Datenpunkt, der nahe am Trainingsdatensatz liegt, das 95%-Konfidenzintervall eine geringe Amplitude aufweist. Immer wenn eine Stichprobe weit von den Trainingsdaten entfernt liegt, ist die Vorhersage unseres Modells weniger genau und die Modellvorhersage ist weniger präzise (höhere Unsicherheit).

Beispiel mit verrauschten Zielwerten

Wir können ein ähnliches Experiment wiederholen, indem wir diesmal zusätzliches Rauschen zum Zielwert hinzufügen. Dies ermöglicht es uns, die Auswirkung des Rauschens auf das angepasste Modell zu sehen.

Wir fügen dem Zielwert zufälliges Gaußsches Rauschen mit einer willkürlichen Standardabweichung hinzu.

noise_std = 0.75
y_train_noisy = y_train + rng.normal(loc=0.0, scale=noise_std, size=y_train.shape)

Wir erstellen ein ähnliches Gaußsches Prozessmodell. Zusätzlich zum Kernel geben wir diesmal den Parameter alpha an, der als Varianz eines Gaußschen Rauschens interpretiert werden kann.

gaussian_process = GaussianProcessRegressor(
    kernel=kernel, alpha=noise_std**2, n_restarts_optimizer=9
)
gaussian_process.fit(X_train, y_train_noisy)
mean_prediction, std_prediction = gaussian_process.predict(X, return_std=True)

Lassen Sie uns die mittlere Vorhersage und den Unsicherheitsbereich wie zuvor plotten.

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.errorbar(
    X_train,
    y_train_noisy,
    noise_std,
    linestyle="None",
    color="tab:blue",
    marker=".",
    markersize=10,
    label="Observations",
)
plt.plot(X, mean_prediction, label="Mean prediction")
plt.fill_between(
    X.ravel(),
    mean_prediction - 1.96 * std_prediction,
    mean_prediction + 1.96 * std_prediction,
    color="tab:orange",
    alpha=0.5,
    label=r"95% confidence interval",
)
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("Gaussian process regression on a noisy dataset")

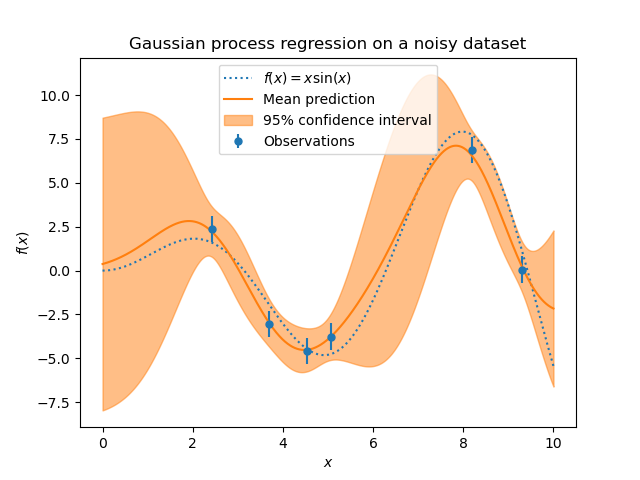
Das Rauschen beeinflusst die Vorhersagen nahe den Trainingsstichproben: Die prädiktive Unsicherheit nahe den Trainingsstichproben ist größer, da wir explizit ein gegebenes Rauschpegelniveau für den Zielwert modellieren, das unabhängig von der Eingabevariable ist.

Verwandte Beispiele

Vergleich von Kernel Ridge und Gauß-Prozess-Regression

Vergleich von Kernel Ridge und Gauß-Prozess-Regression

Fähigkeit der Gauß-Prozess-Regression (GPR) zur Schätzung des Datenrauschpegels

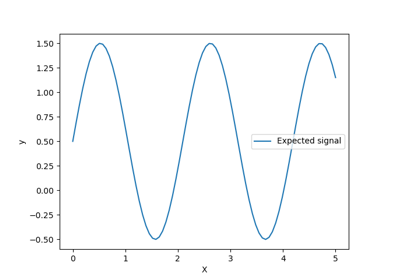
Fähigkeit der Gauß-Prozess-Regression (GPR) zur Schätzung des Datenrauschpegels

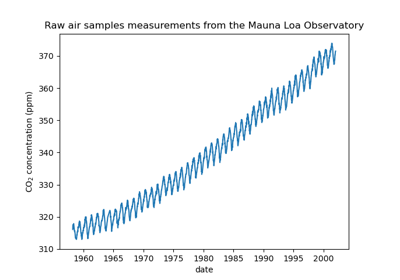
Prognose des CO2-Spiegels im Mona Loa Datensatz mittels Gauß-Prozess-Regression (GPR)

Prognose des CO2-Spiegels im Mona Loa Datensatz mittels Gauß-Prozess-Regression (GPR)

Vorhersageintervalle für Gradient Boosting Regression

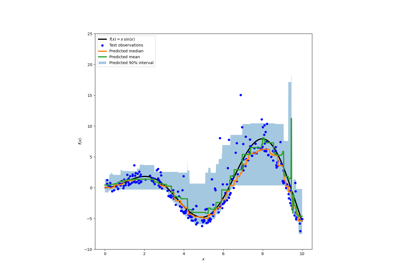
Vorhersageintervalle für Gradient Boosting Regression