Hinweis
Zum Ende springen, um den vollständigen Beispielcode herunterzuladen oder dieses Beispiel über JupyterLite oder Binder in Ihrem Browser auszuführen.
Release Highlights für scikit-learn 1.5#
Wir freuen uns, die Veröffentlichung von scikit-learn 1.5 bekannt zu geben! Viele Fehlerbehebungen und Verbesserungen wurden hinzugefügt, ebenso wie einige wichtige neue Funktionen. Im Folgenden stellen wir die Highlights dieser Version vor. Eine vollständige Liste aller Änderungen finden Sie in den Release Notes.
Um die neueste Version zu installieren (mit pip)
pip install --upgrade scikit-learn
oder mit conda
conda install -c conda-forge scikit-learn
FixedThresholdClassifier: Festlegen des Entscheidungsschwellenwerts eines binären Klassifikators#
Alle binären Klassifikatoren von scikit-learn verwenden einen festen Entscheidungsschwellenwert von 0,5, um Wahrscheinlichkeitsschätzungen (d. h. die Ausgabe von predict_proba) in Klassenvorhersagen umzuwandeln. 0,5 ist jedoch für ein gegebenes Problem fast nie der gewünschte Schwellenwert. FixedThresholdClassifier ermöglicht das Umschließen jedes binären Klassifikators und das Festlegen eines benutzerdefinierten Entscheidungsschwellenwerts.
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split
X, y = make_classification(n_samples=10_000, weights=[0.9, 0.1], random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
classifier_05 = LogisticRegression(C=1e6, random_state=0).fit(X_train, y_train)
_ = ConfusionMatrixDisplay.from_estimator(classifier_05, X_test, y_test)
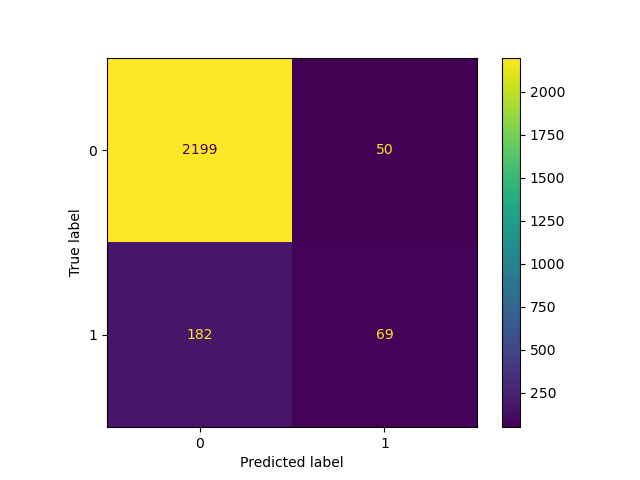
Die Senkung des Schwellenwerts, d. h. die Zulassung von mehr Stichproben, die als positive Klasse klassifiziert werden, erhöht die Anzahl der True Positives auf Kosten von mehr False Positives (wie aus der Konkavität der ROC-Kurve bekannt ist).
from sklearn.model_selection import FixedThresholdClassifier
classifier_01 = FixedThresholdClassifier(classifier_05, threshold=0.1)
classifier_01.fit(X_train, y_train)
_ = ConfusionMatrixDisplay.from_estimator(classifier_01, X_test, y_test)
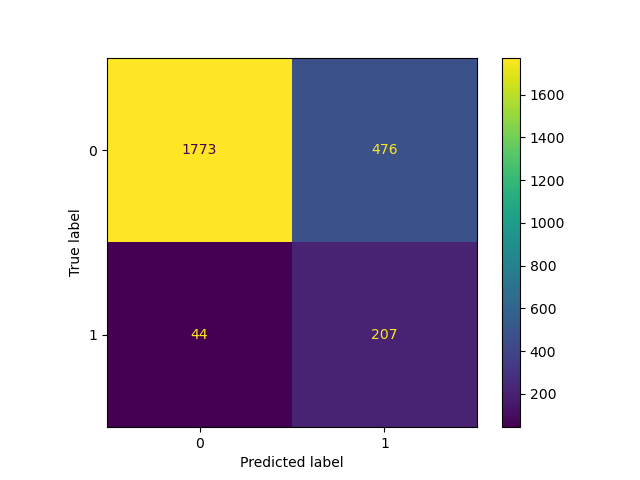
TunedThresholdClassifierCV: Optimierung des Entscheidungsschwellenwerts eines binären Klassifikators#
Der Entscheidungsschwellenwert eines binären Klassifikators kann mithilfe von TunedThresholdClassifierCV optimiert werden, um eine vorgegebene Metrik zu optimieren.
Es ist besonders nützlich, den besten Entscheidungsschwellenwert zu finden, wenn das Modell in einem bestimmten Anwendungsfall eingesetzt werden soll, in dem wir unterschiedliche Gewinne oder Kosten für True Positives, True Negatives, False Positives und False Negatives zuweisen können.
Betrachten wir dies anhand eines willkürlichen Falles, bei dem
jeder True Positive 1 Einheit Gewinn einbringt, z. B. Euro, Jahre gesunden Lebens usw.;
True Negatives nichts einbringen oder kosten;
jeder False Negative 2 kostet;
jeder False Positive 0,1 kostet.
Unsere Metrik quantifiziert den durchschnittlichen Gewinn pro Stichprobe, der durch die folgende Python-Funktion definiert ist
from sklearn.metrics import confusion_matrix
def custom_score(y_observed, y_pred):
tn, fp, fn, tp = confusion_matrix(y_observed, y_pred, normalize="all").ravel()
return tp - 2 * fn - 0.1 * fp
print("Untuned decision threshold: 0.5")
print(f"Custom score: {custom_score(y_test, classifier_05.predict(X_test)):.2f}")
Untuned decision threshold: 0.5
Custom score: -0.12
Es ist interessant festzustellen, dass der durchschnittliche Gewinn pro Vorhersage negativ ist, was bedeutet, dass dieses Entscheidungssystem im Durchschnitt Verluste macht.
Die Optimierung des Schwellenwerts zur Optimierung dieser benutzerdefinierten Metrik ergibt einen kleineren Schwellenwert, der mehr Stichproben als positive Klasse klassifiziert. Infolgedessen verbessert sich der durchschnittliche Gewinn pro Vorhersage.
from sklearn.metrics import make_scorer
from sklearn.model_selection import TunedThresholdClassifierCV
custom_scorer = make_scorer(
custom_score, response_method="predict", greater_is_better=True
)
tuned_classifier = TunedThresholdClassifierCV(
classifier_05, cv=5, scoring=custom_scorer
).fit(X, y)
print(f"Tuned decision threshold: {tuned_classifier.best_threshold_:.3f}")
print(f"Custom score: {custom_score(y_test, tuned_classifier.predict(X_test)):.2f}")
Tuned decision threshold: 0.071
Custom score: 0.04
Wir beobachten, dass die Optimierung des Entscheidungsschwellenwerts ein maschinelles Lernsystem, das im Durchschnitt Verluste macht, in ein vorteilhaftes umwandeln kann.
In der Praxis kann die Definition einer aussagekräftigen anwendungsspezifischen Metrik dazu führen, dass diese Kosten für schlechte Vorhersagen und Gewinne für gute Vorhersagen von zusätzlichen Metadaten abhängen, die für jeden einzelnen Datenpunkt spezifisch sind, wie z. B. der Betrag einer Transaktion in einem Betrugserkennungssystem.
Um dies zu erreichen, nutzt TunedThresholdClassifierCV die Unterstützung für Metadaten-Routing (Benutzerhandbuch für Metadaten-Routing), um komplexe Geschäftsmetriken zu optimieren, wie im Beispiel Nach der Optimierung des Entscheidungsschwellenwerts für kostenempfindliches Lernen beschrieben.
Leistungsverbesserungen in PCA#
PCA verfügt über einen neuen Solver, "covariance_eigh", der für Datensätze mit vielen Datenpunkten und wenigen Merkmalen um eine Größenordnung schneller und speichereffizienter ist als die anderen Solver.
from sklearn.datasets import make_low_rank_matrix
from sklearn.decomposition import PCA
X = make_low_rank_matrix(
n_samples=10_000, n_features=100, tail_strength=0.1, random_state=0
)
pca = PCA(n_components=10, svd_solver="covariance_eigh").fit(X)
print(f"Explained variance: {pca.explained_variance_ratio_.sum():.2f}")
Explained variance: 0.88
Der neue Solver akzeptiert auch spärliche Eingabedaten
Explained variance: 0.13
Der Solver "full" wurde ebenfalls verbessert, um weniger Speicher zu verbrauchen und schnellere Transformationen zu ermöglichen. Die Standardoption svd_solver="auto" nutzt den neuen Solver und kann nun einen geeigneten Solver für spärliche Datensätze auswählen.
Ähnlich wie die meisten anderen PCA-Solver kann der neue Solver "covariance_eigh" GPU-Berechnungen nutzen, wenn die Eingabedaten als PyTorch- oder CuPy-Array übergeben werden, indem die experimentelle Unterstützung für die Array API aktiviert wird.
ColumnTransformer ist abfragbar#
Die Transformer eines ColumnTransformer können nun direkt über die Indizierung nach Namen aufgerufen werden.
import numpy as np
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, StandardScaler
X = np.array([[0, 1, 2], [3, 4, 5]])
column_transformer = ColumnTransformer(
[("std_scaler", StandardScaler(), [0]), ("one_hot", OneHotEncoder(), [1, 2])]
)
column_transformer.fit(X)
print(column_transformer["std_scaler"])
print(column_transformer["one_hot"])
StandardScaler()
OneHotEncoder()
Benutzerdefinierte Imputationsstrategien für SimpleImputer#
SimpleImputer unterstützt nun benutzerdefinierte Strategien für die Imputation unter Verwendung eines aufrufbaren Objekts, das einen Skalarwert aus den nicht fehlenden Werten eines Spaltenvektors berechnet.
from sklearn.impute import SimpleImputer
X = np.array(
[
[-1.1, 1.1, 1.1],
[3.9, -1.2, np.nan],
[np.nan, 1.3, np.nan],
[-0.1, -1.4, -1.4],
[-4.9, 1.5, -1.5],
[np.nan, 1.6, 1.6],
]
)
def smallest_abs(arr):
"""Return the smallest absolute value of a 1D array."""
return np.min(np.abs(arr))
imputer = SimpleImputer(strategy=smallest_abs)
imputer.fit_transform(X)
array([[-1.1, 1.1, 1.1],
[ 3.9, -1.2, 1.1],
[ 0.1, 1.3, 1.1],
[-0.1, -1.4, -1.4],
[-4.9, 1.5, -1.5],
[ 0.1, 1.6, 1.6]])
Paarweise Abstände mit nicht-numerischen Arrays#
pairwise_distances kann nun Abstände zwischen nicht-numerischen Arrays mithilfe einer aufrufbaren Metrik berechnen.
from sklearn.metrics import pairwise_distances
X = ["cat", "dog"]
Y = ["cat", "fox"]
def levenshtein_distance(x, y):
"""Return the Levenshtein distance between two strings."""
if x == "" or y == "":
return max(len(x), len(y))
if x[0] == y[0]:
return levenshtein_distance(x[1:], y[1:])
return 1 + min(
levenshtein_distance(x[1:], y),
levenshtein_distance(x, y[1:]),
levenshtein_distance(x[1:], y[1:]),
)
pairwise_distances(X, Y, metric=levenshtein_distance)
array([[0., 3.],
[3., 2.]])
Gesamtlaufzeit des Skripts: (0 Minuten 0,782 Sekunden)
Verwandte Beispiele
Post-hoc-Anpassung des Cut-off-Punkts der Entscheidungskfunktion
Post-Hoc-Anpassung des Entscheidungsschwellenwerts für kostenempfindliches Lernen
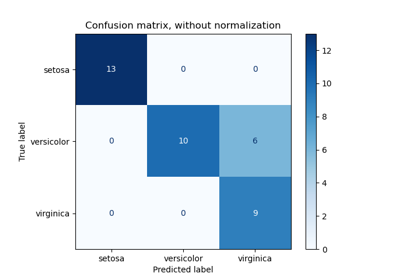
Leistung eines Klassifikators mit Konfusionsmatrix bewerten
