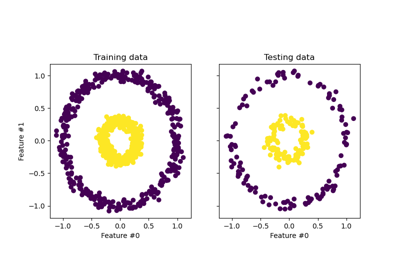
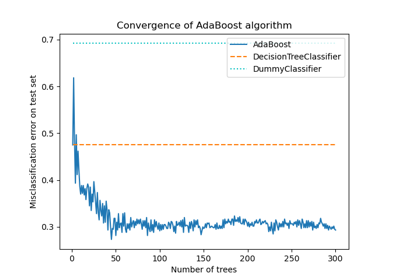
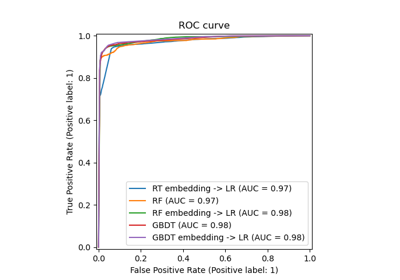
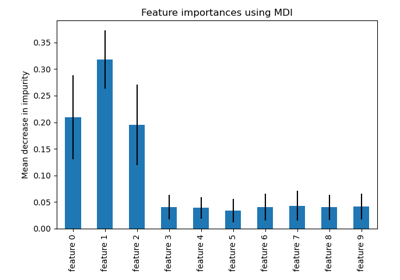
train_test_split#

sklearn.model_selection.train_test_split(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)[Quelle]#

Teilt Arrays oder Matrizen in zufällige Trainings- und Testteilmengen auf.

Schnelle Hilfsfunktion, die die Eingabevalidierung, next(ShuffleSplit().split(X, y)) und die Anwendung auf Eingabedaten in einem einzigen Aufruf für das Aufteilen (und optional Subsampling) von Daten in einer Einzeiligen kombiniert.

Lesen Sie mehr im Benutzerhandbuch.

Parameter:
*arraysSequenz von indexierbaren Objekten mit gleicher Länge / Form[0]

Zulässige Eingaben sind Listen, Numpy-Arrays, SciPy-Sparse-Matrizen oder Pandas-DataFrames.

test_sizefloat oder int, Standardwert=None

Wenn float, sollte zwischen 0,0 und 1,0 liegen und den Anteil des Datensatzes darstellen, der in den Test-Split einbezogen werden soll. Wenn int, stellt die absolute Anzahl der Teststichproben dar. Wenn None, wird der Wert auf das Komplement der Trainingsgröße gesetzt. Wenn train_size ebenfalls None ist, wird er auf 0,25 gesetzt.

train_sizefloat oder int, Standardwert=None

Wenn float, sollte zwischen 0.0 und 1.0 liegen und den Anteil des Datensatzes darstellen, der in die Trainingsaufteilung aufgenommen werden soll. Wenn int, repräsentiert die absolute Anzahl der Trainingsstichproben. Wenn None, wird der Wert automatisch auf das Komplement der Testgröße gesetzt.

random_stateint, RandomState-Instanz oder None, default=None

Steuert das Mischen, das vor der Anwendung des Splits auf die Daten angewendet wird. Geben Sie einen int für reproduzierbare Ausgaben über mehrere Funktionsaufrufe hinweg an. Siehe Glossar.

shufflebool, Standard=True

Ob die Daten vor dem Aufteilen gemischt werden sollen oder nicht. Wenn shuffle=False, muss stratify None sein.

stratifyarray-artig, Standard=None

Wenn nicht None, werden die Daten stratifiziert aufgeteilt, wobei dies als Klassenbezeichnungen verwendet wird. Lesen Sie mehr im Benutzerhandbuch.

Gibt zurück:
splittingListe, Länge=2 * len(arrays)

Liste, die den Trainings-Test-Split der Eingaben enthält.

Hinzugefügt in Version 0.16: Wenn die Eingabe spärlich ist, ist die Ausgabe eine scipy.sparse.csr_matrix. Andernfalls ist der Ausgabetyp derselbe wie der Eingabetyp.

Beispiele

>>> import numpy as np
>>> from sklearn.model_selection import train_test_split
>>> X, y = np.arange(10).reshape((5, 2)), range(5)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7],
       [8, 9]])
>>> list(y)
[0, 1, 2, 3, 4]

>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.33, random_state=42)
...
>>> X_train
array([[4, 5],
       [0, 1],
       [6, 7]])
>>> y_train
[2, 0, 3]
>>> X_test
array([[2, 3],
       [8, 9]])
>>> y_test
[1, 4]

>>> train_test_split(y, shuffle=False)
[[0, 1, 2], [3, 4]]

>>> from sklearn import datasets
>>> iris = datasets.load_iris(as_frame=True)
>>> X, y = iris['data'], iris['target']
>>> X.head()
    sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)
0                5.1               3.5                1.4               0.2
1                4.9               3.0                1.4               0.2
2                4.7               3.2                1.3               0.2
3                4.6               3.1                1.5               0.2
4                5.0               3.6                1.4               0.2
>>> y.head()
0    0
1    0
2    0
3    0
4    0
...

>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, test_size=0.33, random_state=42)
...
>>> X_train.head()
    sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)
96                 5.7               2.9                4.2               1.3
105                7.6               3.0                6.6               2.1
66                 5.6               3.0                4.5               1.5
0                  5.1               3.5                1.4               0.2
122                7.7               2.8                6.7               2.0
>>> y_train.head()
96     1
105    2
66     1
0      0
122    2
...
>>> X_test.head()
    sepal length (cm)  sepal width (cm)  petal length (cm)  petal width (cm)
73                 6.1               2.8                4.7               1.2
18                 5.7               3.8                1.7               0.3
118                7.7               2.6                6.9               2.3
78                 6.0               2.9                4.5               1.5
76                 6.8               2.8                4.8               1.4
>>> y_test.head()
73     1
18     0
118    2
78     1
76     1
...
Auf dieser Seite

Diese Seite