Matern#
- class sklearn.gaussian_process.kernels.Matern(length_scale=1.0, length_scale_bounds=(1e-05, 100000.0), nu=1.5)[Quelle]#
Matern-Kernel.
Die Klasse der Matern-Kerne ist eine Verallgemeinerung des
RBF. Sie hat einen zusätzlichen Parameter \(\nu\), der die Glattheit der resultierenden Funktion steuert. Je kleiner \(\nu\) ist, desto weniger glatt ist die approximierte Funktion. Wenn \(\nu\rightarrow\infty\), wird der Kern äquivalent zumRBF-Kern. Wenn \(\nu = 1/2\), ist der Matérn-Kern identisch mit dem absolut exponentiellen Kern. Wichtige Zwischenwerte sind \(\nu=1.5\) (einmal differenzierbare Funktionen) und \(\nu=2.5\) (zweimal differenzierbare Funktionen).Der Kern ist gegeben durch
\[k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg( \frac{\sqrt{2\nu}}{l} d(x_i , x_j ) \Bigg)^\nu K_\nu\Bigg( \frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)\]wobei \(d(\cdot,\cdot)\) die euklidische Distanz ist, \(K_{\nu}(\cdot)\) eine modifizierte Besselfunktion und \(\Gamma(\cdot)\) die Gammafunktion ist. Siehe [1], Kapitel 4, Abschnitt 4.2, für Details zu den verschiedenen Varianten des Matérn-Kerns.
Lesen Sie mehr im Benutzerhandbuch.
Hinzugefügt in Version 0.18.
- Parameter:
- length_scalefloat oder ndarray der Form (n_features,), Standardwert=1.0
Die Skalenlänge des Kerns. Wenn es sich um einen Float handelt, wird ein isotroper Kern verwendet. Wenn es sich um ein Array handelt, wird ein anisotroper Kern verwendet, bei dem jede Dimension von l die Skalenlänge der jeweiligen Merkmalsdimension definiert.
- length_scale_boundsPaar von Floats >= 0 oder „fixed“, Standardwert=(1e-5, 1e5)
Die untere und obere Grenze für ‘length_scale’. Wenn auf „fixed“ gesetzt, kann ‘length_scale’ während des Hyperparameter-Tunings nicht geändert werden.
- nufloat, Standardwert=1.5
Der Parameter nu, der die Glattheit der gelernten Funktion steuert. Je kleiner nu, desto weniger glatt ist die approximierte Funktion. Für nu=inf wird der Kern äquivalent zum RBF-Kern und für nu=0.5 zum absolut exponentiellen Kern. Wichtige Zwischenwerte sind nu=1.5 (einmal differenzierbare Funktionen) und nu=2.5 (zweimal differenzierbare Funktionen). Beachten Sie, dass Werte von nu, die nicht in [0.5, 1.5, 2.5, inf] liegen, erhebliche höhere Rechenkosten verursachen (ca. 10-mal höher), da sie die Auswertung der modifizierten Besselfunktion erfordern. Im Gegensatz zu l wird nu fest auf seinen Anfangswert gesetzt und nicht optimiert.
Referenzen
Beispiele
>>> from sklearn.datasets import load_iris >>> from sklearn.gaussian_process import GaussianProcessClassifier >>> from sklearn.gaussian_process.kernels import Matern >>> X, y = load_iris(return_X_y=True) >>> kernel = 1.0 * Matern(length_scale=1.0, nu=1.5) >>> gpc = GaussianProcessClassifier(kernel=kernel, ... random_state=0).fit(X, y) >>> gpc.score(X, y) 0.9866 >>> gpc.predict_proba(X[:2,:]) array([[0.8513, 0.0368, 0.1117], [0.8086, 0.0693, 0.1220]])
- __call__(X, Y=None, eval_gradient=False)[Quelle]#
Gibt den Kernel k(X, Y) und optional seinen Gradienten zurück.
- Parameter:
- Xndarray mit Form (n_samples_X, n_features)
Linkes Argument des zurückgegebenen Kernels k(X, Y)
- Yndarray mit Form (n_samples_Y, n_features), Standardwert=None
Rechtes Argument des zurückgegebenen Kernels k(X, Y). Wenn None, wird stattdessen k(X, X) ausgewertet.
- eval_gradientbool, Standardwert=False
Bestimmt, ob der Gradient bezüglich des Logarithmus des Kernel-Hyperparameters berechnet wird. Nur unterstützt, wenn Y None ist.
- Gibt zurück:
- Kndarray mit Form (n_samples_X, n_samples_Y)
Kernel k(X, Y)
- K_gradientndarray mit Form (n_samples_X, n_samples_X, n_dims), optional
Der Gradient des Kernels k(X, X) bezüglich des Logarithmus des Hyperparameters des Kernels. Nur zurückgegeben, wenn
eval_gradientTrue ist.
- property bounds#
Gibt die log-transformierten Grenzen für theta zurück.
- Gibt zurück:
- boundsndarray mit Form (n_dims, 2)
Die log-transformierten Grenzen für die Hyperparameter theta des Kernels
- clone_with_theta(theta)[Quelle]#
Gibt eine Kopie von self mit den angegebenen Hyperparametern theta zurück.
- Parameter:
- thetandarray mit Form (n_dims,)
Die Hyperparameter
- diag(X)[Quelle]#
Gibt die Diagonale des Kernels k(X, X) zurück.
Das Ergebnis dieser Methode ist identisch mit np.diag(self(X)); sie kann jedoch effizienter ausgewertet werden, da nur die Diagonale ausgewertet wird.
- Parameter:
- Xndarray mit Form (n_samples_X, n_features)
Linkes Argument des zurückgegebenen Kernels k(X, Y)
- Gibt zurück:
- K_diagndarray mit Form (n_samples_X,)
Diagonale des Kerns k(X, X)
- get_params(deep=True)[Quelle]#
Parameter dieses Kernels abrufen.
- Parameter:
- deepbool, default=True
Wenn True, werden die Parameter für diesen Schätzer und die enthaltenen Unterobjekte, die Schätzer sind, zurückgegeben.
- Gibt zurück:
- paramsdict
Parameternamen, zugeordnet ihren Werten.
- property hyperparameters#
Gibt eine Liste aller Spezifikationen von Hyperparametern zurück.
- property n_dims#
Gibt die Anzahl der nicht-festen Hyperparameter des Kernels zurück.
- property requires_vector_input#
Gibt zurück, ob der Kernel auf Vektoren mit fester Länge oder generischen Objekten definiert ist. Standardmäßig True aus Kompatibilitätsgründen.
- set_params(**params)[Quelle]#
Parameter dieses Kernels setzen.
Die Methode funktioniert sowohl bei einfachen Kernels als auch bei verschachtelten Kernels. Letztere haben Parameter der Form
<component>__<parameter>, sodass es möglich ist, jede Komponente eines verschachtelten Objekts zu aktualisieren.- Gibt zurück:
- self
- property theta#
Gibt die (abgeflachten, log-transformierten) nicht-festen Hyperparameter zurück.
Beachten Sie, dass theta typischerweise die log-transformierten Werte der Hyperparameter des Kernels sind, da diese Darstellung des Suchraums besser für die Hyperparameter-Suche geeignet ist, da Hyperparameter wie Längen-Skalen natürlich auf einer logarithmischen Skala liegen.
- Gibt zurück:
- thetandarray mit Form (n_dims,)
Die nicht-festen, log-transformierten Hyperparameter des Kernels
Galeriebeispiele#
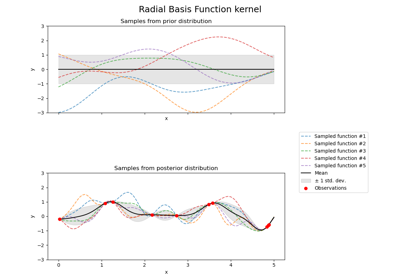
Illustration von Prior und Posterior Gauß-Prozess für verschiedene Kerne