NMF#
- class sklearn.decomposition.NMF(n_components='auto', *, init=None, solver='cd', beta_loss='frobenius', tol=0.0001, max_iter=200, random_state=None, alpha_W=0.0, alpha_H='same', l1_ratio=0.0, verbose=0, shuffle=False)[Quelle]#
Non-Negative Matrix Factorization (NMF).
Finde zwei nicht-negative Matrizen, d.h. Matrizen mit allen nicht-negativen Elementen, (W, H), deren Produkt die nicht-negative Matrix X approximiert. Diese Faktorisierung kann zum Beispiel zur Dimensionsreduktion, Quellentrennung oder Extraktion von Themen verwendet werden.
Die Zielfunktion ist
\[ \begin{align}\begin{aligned}L(W, H) &= 0.5 * ||X - WH||_{loss}^2\\ &+ alpha\_W * l1\_ratio * n\_features * ||vec(W)||_1\\ &+ alpha\_H * l1\_ratio * n\_samples * ||vec(H)||_1\\ &+ 0.5 * alpha\_W * (1 - l1\_ratio) * n\_features * ||W||_{Fro}^2\\ &+ 0.5 * alpha\_H * (1 - l1\_ratio) * n\_samples * ||H||_{Fro}^2,\end{aligned}\end{align} \]wobei \(||A||_{Fro}^2 = \sum_{i,j} A_{ij}^2\) (Frobenius-Norm) und \(||vec(A)||_1 = \sum_{i,j} abs(A_{ij})\) (Elementweise L1-Norm).
Die allgemeine Norm \(||X - WH||_{loss}\) kann die Frobenius-Norm oder eine andere unterstützte Beta-Divergenz-Verlustfunktion darstellen. Die Wahl zwischen den Optionen wird durch den Parameter
beta_lossgesteuert.Die Regularisierungsterme werden mit
n_featuresfürWund mitn_samplesfürHskaliert, um ihre Auswirkung im Verhältnis zueinander und zum Datenanpassungsterm so unabhängig wie möglich von der Größen_samplesdes Trainingsdatensatzes auszubalancieren.Die Zielfunktion wird mit einer alternierenden Minimierung von W und H minimiert.
Beachten Sie, dass die transformierten Daten W und die Komponentenmatrix H genannt werden. In der NMF-Literatur ist die Namenskonvention normalerweise umgekehrt, da die Datenmatrix X transponiert ist.
Lesen Sie mehr im Benutzerhandbuch.
- Parameter:
- n_componentsint oder {‘auto’} oder None, default=’auto’
Anzahl der Komponenten. Wenn
None, werden alle Merkmale beibehalten. Wennn_components='auto', wird die Anzahl der Komponenten automatisch aus den Formen von W oder H abgeleitet.Geändert in Version 1.4: `auto`-Wert hinzugefügt.
Geändert in Version 1.6: Standardwert von
Noneauf'auto'geändert.- init{‘random’, ‘nndsvd’, ‘nndsvda’, ‘nndsvdar’, ‘custom’}, default=None
Methode zur Initialisierung des Verfahrens. Gültige Optionen
None: ‚nndsvda‘, wenn n_components <= min(n_samples, n_features), ansonsten zufällig.'random': nicht-negative Zufallsmatrizen, skaliert mit:sqrt(X.mean() / n_components)'nndsvd': Nonnegative Double Singular Value Decomposition (NNDSVD) Initialisierung (besser für Sparsity)'nndsvda': NNDSVD mit Nullen, die mit dem Durchschnitt von X gefüllt sind (besser, wenn Sparsity nicht gewünscht ist)'nndsvdar': NNDSVD mit Nullen, die mit kleinen Zufallswerten gefüllt sind (generell schneller, weniger genaue Alternative zu NNDSVDa, wenn Sparsity nicht gewünscht ist)'custom': Verwenden Sie benutzerdefinierte MatrizenWundH, die beide bereitgestellt werden müssen.
Geändert in Version 1.1: Wenn
init=Noneund n_components kleiner als n_samples und n_features ist, wird standardmäßignndsvdaanstelle vonnndsvdverwendet.- solver{‘cd’, ‘mu’}, standard=‘cd’
Numerischer Solver, der verwendet werden soll
‘cd’ ist ein Coordinate Descent Solver.
‘mu’ ist ein Multiplicative Update Solver.
Hinzugefügt in Version 0.17: Coordinate Descent Solver.
Hinzugefügt in Version 0.19: Multiplicative Update Solver.
- beta_lossfloat oder {‘frobenius’, ‘kullback-leibler’, ‘itakura-saito’}, default=’frobenius’
Zu minimierende Beta-Divergenz, die den Abstand zwischen X und dem Skalarprodukt WH misst. Beachten Sie, dass Werte, die sich von ‚frobenius‘ (oder 2) und ‚kullback-leibler‘ (oder 1) unterscheiden, zu deutlich langsameren Fits führen. Beachten Sie, dass für beta_loss <= 0 (oder ‚itakura-saito‘) die Eingabematrix X keine Nullen enthalten darf. Nur für den Solver ‚mu‘ verwendet.
Hinzugefügt in Version 0.19.
- tolfloat, Standard=1e-4
Toleranz der Abbruchbedingung.
- max_iterint, Standard=200
Maximale Anzahl von Iterationen vor Zeitüberschreitung.
- random_stateint, RandomState-Instanz oder None, default=None
Verwendet für die Initialisierung (wenn
init== ‚nndsvdar‘ oder ‚random‘) und im Coordinate Descent. Übergeben Sie eine Ganzzahl für reproduzierbare Ergebnisse über mehrere Funktionsaufrufe hinweg. Siehe Glossar.- alpha_Wfloat, default=0.0
Konstante, die die Regularisierungsterme von
Wmultipliziert. Setzen Sie sie auf Null (Standardwert), um keine Regularisierung beiWzu haben.Hinzugefügt in Version 1.0.
- alpha_Hfloat oder “same”, default=”same”
Konstante, die die Regularisierungsterme von
Hmultipliziert. Setzen Sie sie auf Null, um keine Regularisierung beiHzu haben. Wenn “same” (Standardwert), nimmt sie denselben Wert wiealpha_Wan.Hinzugefügt in Version 1.0.
- l1_ratiofloat, default=0.0
Der Regularisierungs-Mixing-Parameter, mit 0 <= l1_ratio <= 1. Für l1_ratio = 0 ist die Strafe eine elementweise L2-Strafe (auch Frobenius-Norm genannt). Für l1_ratio = 1 ist es eine elementweise L1-Strafe. Für 0 < l1_ratio < 1 ist die Strafe eine Kombination aus L1 und L2.
Hinzugefügt in Version 0.17: Regularisierungsparameter l1_ratio, der im Coordinate Descent Solver verwendet wird.
- verboseint, default=0
Ob die Ausgabe ausführlich sein soll.
- shufflebool, default=False
Wenn wahr, wird die Reihenfolge der Koordinaten im CD-Solver zufällig gewählt.
Hinzugefügt in Version 0.17: shuffle-Parameter, der im Coordinate Descent Solver verwendet wird.
- Attribute:
- components_ndarray der Form (n_components, n_features)
Faktorisierungsmatrix, manchmal auch „Wörterbuch“ genannt.
- n_components_int
Die Anzahl der Komponenten. Sie ist gleich dem Parameter
n_components, wenn dieser angegeben wurde. Andernfalls entspricht sie der Anzahl der Merkmale.- reconstruction_err_float
Frobenius-Norm der Matrixdifferenz oder Beta-Divergenz zwischen den Trainingsdaten
Xund den rekonstruierten DatenWHaus dem angepassten Modell.- n_iter_int
Tatsächliche Anzahl der Iterationen.
- n_features_in_int
Anzahl der während des fits gesehenen Merkmale.
Hinzugefügt in Version 0.24.
- feature_names_in_ndarray mit Form (
n_features_in_,) Namen der während fit gesehenen Merkmale. Nur definiert, wenn
XMerkmalnamen hat, die alle Zeichenketten sind.Hinzugefügt in Version 1.0.
Siehe auch
DictionaryLearningFindet ein Dictionary, das Daten spärlich kodiert.
MiniBatchSparsePCAMini-Batch Sparse Principal Components Analysis.
PCAHauptkomponentenanalyse.
SparseCoderFindet eine spärliche Darstellung von Daten aus einem festen, vordefinierten Dictionary.
SparsePCASpärliche Hauptkomponentenanalyse.
TruncatedSVDDimensionsreduktion mittels abgeschnittener SVD.
Referenzen
[1]„Fast local algorithms for large scale nonnegative matrix and tensor factorizations“ Cichocki, Andrzej, und P. H. A. N. Anh-Huy. IEICE transactions on fundamentals of electronics, communications and computer sciences 92.3: 708-721, 2009.
[2]„Algorithms for nonnegative matrix factorization with the beta-divergence“ Fevotte, C., & Idier, J. (2011). Neural Computation, 23(9).
Beispiele
>>> import numpy as np >>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]]) >>> from sklearn.decomposition import NMF >>> model = NMF(n_components=2, init='random', random_state=0) >>> W = model.fit_transform(X) >>> H = model.components_
- fit(X, y=None, **params)[Quelle]#
Lernen Sie ein NMF-Modell für die Daten X.
- Parameter:
- X{array-like, sparse matrix} der Form (n_samples, n_features)
Trainingsvektor, wobei
n_samplesdie Anzahl der Stichproben undn_featuresdie Anzahl der Merkmale ist.- yIgnoriert
Wird nicht verwendet, ist aber aus Gründen der API-Konsistenz per Konvention vorhanden.
- **paramskwargs
Parameter (Stichwortargumente) und Werte, die an die fit_transform-Instanz übergeben werden.
- Gibt zurück:
- selfobject
Gibt die Instanz selbst zurück.
- fit_transform(X, y=None, W=None, H=None)[Quelle]#
Lernen Sie ein NMF-Modell für die Daten X und geben Sie die transformierten Daten zurück.
Dies ist effizienter als fit gefolgt von transform aufzurufen.
- Parameter:
- X{array-like, sparse matrix} der Form (n_samples, n_features)
Trainingsvektor, wobei
n_samplesdie Anzahl der Stichproben undn_featuresdie Anzahl der Merkmale ist.- yIgnoriert
Wird nicht verwendet, ist aber aus Gründen der API-Konsistenz per Konvention vorhanden.
- Warray-like von Form (n_samples, n_components), default=None
Wenn
init='custom', wird es als anfänglicher Schätzwert für die Lösung verwendet. WennNone, wird die ininitangegebene Initialisierungsmethode verwendet.- Harray-like von Form (n_components, n_features), default=None
Wenn
init='custom', wird es als anfänglicher Schätzwert für die Lösung verwendet. WennNone, wird die ininitangegebene Initialisierungsmethode verwendet.
- Gibt zurück:
- Wndarray von Form (n_samples, n_components)
Transformierte Daten.
- get_feature_names_out(input_features=None)[Quelle]#
Holt die Ausgabemerkmale für die Transformation.
Die Feature-Namen werden mit dem kleingeschriebenen Klassennamen präfixiert. Wenn der Transformer z.B. 3 Features ausgibt, dann sind die Feature-Namen:
["klassenname0", "klassenname1", "klassenname2"].- Parameter:
- input_featuresarray-like von str oder None, default=None
Wird nur verwendet, um die Feature-Namen mit den in
fitgesehenen Namen zu validieren.
- Gibt zurück:
- feature_names_outndarray von str-Objekten
Transformierte Merkmalnamen.
- get_metadata_routing()[Quelle]#
Holt das Metadaten-Routing dieses Objekts.
Bitte prüfen Sie im Benutzerhandbuch, wie der Routing-Mechanismus funktioniert.
- Gibt zurück:
- routingMetadataRequest
Ein
MetadataRequest, der Routing-Informationen kapselt.
- get_params(deep=True)[Quelle]#
Holt Parameter für diesen Schätzer.
- Parameter:
- deepbool, default=True
Wenn True, werden die Parameter für diesen Schätzer und die enthaltenen Unterobjekte, die Schätzer sind, zurückgegeben.
- Gibt zurück:
- paramsdict
Parameternamen, zugeordnet ihren Werten.
- inverse_transform(X)[Quelle]#
Daten zurück in ihren ursprünglichen Raum transformieren.
Hinzugefügt in Version 0.18.
- Parameter:
- X{ndarray, sparse matrix} der Form (n_samples, n_components)
Transformierte Datenmatrix.
- Gibt zurück:
- X_originalndarray von der Form (n_samples, n_features)
Gibt eine Datenmatrix in der ursprünglichen Form zurück.
- set_output(*, transform=None)[Quelle]#
Ausgabecontainer festlegen.
Siehe Einführung in die set_output API für ein Beispiel zur Verwendung der API.
- Parameter:
- transform{“default”, “pandas”, “polars”}, default=None
Konfiguriert die Ausgabe von
transformundfit_transform."default": Standardausgabeformat eines Transformers"pandas": DataFrame-Ausgabe"polars": Polars-AusgabeNone: Die Transformationskonfiguration bleibt unverändert
Hinzugefügt in Version 1.4: Die Option
"polars"wurde hinzugefügt.
- Gibt zurück:
- selfestimator instance
Schätzer-Instanz.
- set_params(**params)[Quelle]#
Setzt die Parameter dieses Schätzers.
Die Methode funktioniert sowohl bei einfachen Schätzern als auch bei verschachtelten Objekten (wie
Pipeline). Letztere haben Parameter der Form<component>__<parameter>, so dass es möglich ist, jede Komponente eines verschachtelten Objekts zu aktualisieren.- Parameter:
- **paramsdict
Schätzer-Parameter.
- Gibt zurück:
- selfestimator instance
Schätzer-Instanz.
- transform(X)[Quelle]#
Transformieren Sie die Daten X gemäß dem angepassten NMF-Modell.
- Parameter:
- X{array-like, sparse matrix} der Form (n_samples, n_features)
Trainingsvektor, wobei
n_samplesdie Anzahl der Stichproben undn_featuresdie Anzahl der Merkmale ist.
- Gibt zurück:
- Wndarray von Form (n_samples, n_components)
Transformierte Daten.
Galeriebeispiele#
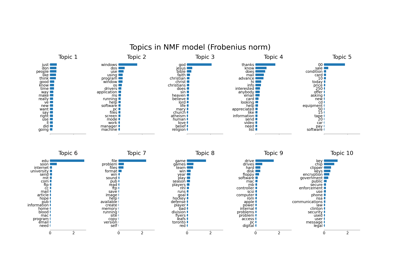
Themenextraktion mit Non-negative Matrix Factorization und Latent Dirichlet Allocation
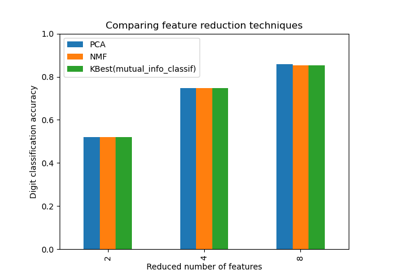
Dimensionsreduktion auswählen mit Pipeline und GridSearchCV
