EllipticEnvelope#
- class sklearn.covariance.EllipticEnvelope(*, store_precision=True, assume_centered=False, support_fraction=None, contamination=0.1, random_state=None)[source]#
Objekt zur Erkennung von Ausreißern in einem Gauß'schen Datensatz.
Lesen Sie mehr im Benutzerhandbuch.
- Parameter:
- store_precisionbool, Standard=True
Gibt an, ob die geschätzte Präzision gespeichert wird.
- assume_centeredbool, Standard=False
Wenn True, wird die Basis für robuste Lage- und Kovarianzschätzungen berechnet und eine Kovarianzschätzung daraus neu berechnet, ohne die Daten zu zentrieren. Nützlich für die Arbeit mit Daten, deren Mittelwert signifikant Null ist, aber nicht exakt Null. Wenn False, werden die robusten Lage- und Kovarianzschätzungen direkt mit dem FastMCD-Algorithmus ohne zusätzliche Behandlung berechnet.
- support_fractionfloat, Standard=None
Der Anteil der Punkte, die in die Basis der rohen MCD-Schätzung einbezogen werden sollen. Wenn None, wird der Mindestwert von support_fraction innerhalb des Algorithmus verwendet:
(n_samples + n_features + 1) / 2 * n_samples. Bereich ist (0, 1).- contaminationfloat, Standard=0.1
Der Grad der Kontamination des Datensatzes, d.h. der Anteil der Ausreißer im Datensatz. Bereich ist (0, 0.5].
- random_stateint, RandomState-Instanz oder None, default=None
Bestimmt den Pseudo-Zufallszahlengenerator zum Mischen der Daten. Übergeben Sie eine Ganzzahl für reproduzierbare Ergebnisse über mehrere Funktionsaufrufe hinweg. Siehe Glossar.
- Attribute:
- location_ndarray der Form (n_features,)
Geschätzte robuste Lage.
- covariance_ndarray der Form (n_features, n_features)
Geschätzte robuste Kovarianzmatrix.
- precision_ndarray der Form (n_features, n_features)
Geschätzte inverse Pseudomatrix. (nur gespeichert, wenn store_precision True ist)
- support_ndarray von Form (n_samples,)
Eine Maske der Beobachtungen, die zur Berechnung der robusten Schätzungen von Lage und Form verwendet wurden.
- offset_float
Offset, der zur Definition der Entscheidungsfunktion aus den rohen Scores verwendet wird. Wir haben die Beziehung:
decision_function = score_samples - offset_. Der Offset hängt vom Kontaminationsparameter ab und ist so definiert, dass wir die erwartete Anzahl von Ausreißern (Stichproben mit Entscheidungsfunktion < 0) im Training erhalten.Hinzugefügt in Version 0.20.
- raw_location_ndarray von Form (n_features,)
Die rohe robuste geschätzte Lage vor Korrektur und Neuberechnung der Gewichte.
- raw_covariance_ndarray von Form (n_features, n_features)
Die rohe robuste geschätzte Kovarianz vor Korrektur und Neuberechnung der Gewichte.
- raw_support_ndarray von Form (n_samples,)
Eine Maske der Beobachtungen, die zur Berechnung der rohen robusten Schätzungen von Lage und Form verwendet wurden, vor Korrektur und Neuberechnung der Gewichte.
- dist_ndarray von Form (n_samples,)
Mahalanobis-Distanzen der Trainingsstichprobe (auf der
fitaufgerufen wird).- n_features_in_int
Anzahl der während des fits gesehenen Merkmale.
Hinzugefügt in Version 0.24.
- feature_names_in_ndarray mit Form (
n_features_in_,) Namen der während fit gesehenen Merkmale. Nur definiert, wenn
XMerkmalnamen hat, die alle Zeichenketten sind.Hinzugefügt in Version 1.0.
Siehe auch
EmpiricalCovarianceMaximale Likelihood Kovarianz-Schätzer.
GraphicalLassoSchätzung der dünnen Kovarianz mit einem l1-penalisierten Schätzer.
LedoitWolfLedoitWolf-Schätzer.
MinCovDetMinimum Covariance Determinant (robuster Schätzer der Kovarianz).
OASOracle Approximating Shrinkage Estimator.
ShrunkCovarianceKovarianz-Schätzer mit Schrumpfung.
Anmerkungen
Die Ausreißererkennung anhand von Kovarianzschätzungen kann in hochdimensionalen Umgebungen fehlschlagen oder nicht gut funktionieren. Insbesondere sollte man immer darauf achten, mit
n_samples > n_features ** 2zu arbeiten.Referenzen
[1]Rousseeuw, P.J., Van Driessen, K. „A fast algorithm for the minimum covariance determinant estimator“ Technometrics 41(3), 212 (1999)
Beispiele
>>> import numpy as np >>> from sklearn.covariance import EllipticEnvelope >>> true_cov = np.array([[.8, .3], ... [.3, .4]]) >>> X = np.random.RandomState(0).multivariate_normal(mean=[0, 0], ... cov=true_cov, ... size=500) >>> cov = EllipticEnvelope(random_state=0).fit(X) >>> # predict returns 1 for an inlier and -1 for an outlier >>> cov.predict([[0, 0], ... [3, 3]]) array([ 1, -1]) >>> cov.covariance_ array([[0.8102, 0.2736], [0.2736, 0.3330]]) >>> cov.location_ array([0.0769 , 0.0397])
- correct_covariance(data)[source]#
Wendet eine Korrektur auf die rohen Minimum Covariance Determinant Schätzungen an.
Korrektur unter Verwendung des asymptotischen Korrekturfaktors, der von [Croux1999] abgeleitet wurde.
- Parameter:
- dataarray-like of shape (n_samples, n_features)
Die Datenmatrix mit p Merkmalen und n Stichproben. Der Datensatz muss derjenige sein, der zur Berechnung der rohen Schätzungen verwendet wurde.
- Gibt zurück:
- covariance_correctedndarray von Form (n_features, n_features)
Korrigierte robuste Kovarianzschätzung.
Referenzen
[Croux1999]Influence Function and Efficiency of the Minimum Covariance Determinant Scatter Matrix Estimator, 1999, Journal of Multivariate Analysis, Volume 71, Issue 2, Seiten 161-190
- decision_function(X)[source]#
Berechnet die Entscheidungsfunktion der gegebenen Beobachtungen.
- Parameter:
- Xarray-like der Form (n_samples, n_features)
Die Datenmatrix.
- Gibt zurück:
- decisionndarray von Form (n_samples,)
Entscheidungsfunktion der Stichproben. Sie ist gleich den verschobenen Mahalanobis-Distanzen. Der Schwellenwert für Ausreißer ist 0, was die Kompatibilität mit anderen Ausreißererkennungsalgorithmen gewährleistet.
- error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)[source]#
Berechnet den mittleren quadratischen Fehler zwischen zwei Kovarianzschätzern.
- Parameter:
- comp_covarray-like der Form (n_features, n_features)
Die zu vergleichende Kovarianz.
- norm{„frobenius“, „spectral“}, Standard=„frobenius“
Die Art der Norm, die zur Berechnung des Fehlers verwendet wird. Verfügbare Fehlertypen: - „frobenius“ (Standard): sqrt(tr(A^t.A)) - „spectral“: sqrt(max(Eigenwerte(A^t.A))), wobei A der Fehler ist
(comp_cov - self.covariance_).- scalingbool, Standard=True
Wenn True (Standard), wird die quadrierte Fehlernorm durch n_features geteilt. Wenn False, wird die quadrierte Fehlernorm nicht skaliert.
- squaredbool, Standard=True
Ob die quadrierte Fehlernorm oder die Fehlernorm berechnet werden soll. Wenn True (Standard), wird die quadrierte Fehlernorm zurückgegeben. Wenn False, wird die Fehlernorm zurückgegeben.
- Gibt zurück:
- resultfloat
Der mittlere quadratische Fehler (im Sinne der Frobenius-Norm) zwischen
selfundcomp_covKovarianzschätzern.
- fit(X, y=None)[source]#
Passt das EllipticEnvelope-Modell an.
- Parameter:
- Xarray-like der Form (n_samples, n_features)
Trainingsdaten.
- yIgnoriert
Wird nicht verwendet, ist aber aus Gründen der API-Konsistenz per Konvention vorhanden.
- Gibt zurück:
- selfobject
Gibt die Instanz selbst zurück.
- fit_predict(X, y=None, **kwargs)[source]#
Führt die Anpassung an X durch und gibt Labels für X zurück.
Gibt -1 für Ausreißer und 1 für Inlier zurück.
- Parameter:
- X{array-like, sparse matrix} der Form (n_samples, n_features)
Die Eingabestichproben.
- yIgnoriert
Wird nicht verwendet, ist aber aus Gründen der API-Konsistenz per Konvention vorhanden.
- **kwargsdict
Argumente, die an
fitübergeben werden sollen.Hinzugefügt in Version 1.4.
- Gibt zurück:
- yndarray der Form (n_samples,)
1 für Inlier, -1 für Ausreißer.
- get_metadata_routing()[source]#
Holt das Metadaten-Routing dieses Objekts.
Bitte prüfen Sie im Benutzerhandbuch, wie der Routing-Mechanismus funktioniert.
- Gibt zurück:
- routingMetadataRequest
Ein
MetadataRequest, der Routing-Informationen kapselt.
- get_params(deep=True)[source]#
Holt Parameter für diesen Schätzer.
- Parameter:
- deepbool, default=True
Wenn True, werden die Parameter für diesen Schätzer und die enthaltenen Unterobjekte, die Schätzer sind, zurückgegeben.
- Gibt zurück:
- paramsdict
Parameternamen, zugeordnet ihren Werten.
- get_precision()[source]#
Getter für die Präzisionsmatrix.
- Gibt zurück:
- precision_array-like der Form (n_features, n_features)
Die Präzisionsmatrix, die dem aktuellen Kovarianzobjekt zugeordnet ist.
- mahalanobis(X)[source]#
Berechnet die quadrierten Mahalanobis-Abstände gegebener Beobachtungen.
Ein detailliertes Beispiel dafür, wie Ausreißer den Mahalanobis-Abstand beeinflussen, finden Sie unter Robuste Kovarianzschätzung und die Relevanz von Mahalanobis-Abständen.
- Parameter:
- Xarray-like der Form (n_samples, n_features)
Die Beobachtungen, deren Mahalanobis-Abstände wir berechnen. Es wird davon ausgegangen, dass die Beobachtungen aus derselben Verteilung stammen wie die in fit verwendeten Daten.
- Gibt zurück:
- distndarray der Form (n_samples,)
Quadrierte Mahalanobis-Abstände der Beobachtungen.
- predict(X)[source]#
Sagt Labels (1 Inlier, -1 Ausreißer) von X gemäß dem angepassten Modell voraus.
- Parameter:
- Xarray-like der Form (n_samples, n_features)
Die Datenmatrix.
- Gibt zurück:
- is_inlierndarray von Form (n_samples,)
Gibt -1 für Anomalien/Ausreißer und +1 für Inlier zurück.
- reweight_covariance(data)[source]#
Berechnet die rohen Minimum Covariance Determinant Schätzungen neu.
Berechnet die Beobachtungen mit der Methode von Rousseeuw neu (entspricht dem Entfernen von Ausreißern aus dem Datensatz, bevor Lage- und Kovarianzschätzungen berechnet werden), wie in [RVDriessen] beschrieben.
Korrigiert die neu gewichtete Kovarianz, um sie für die Normalverteilung konsistent zu machen, gemäß [Croux1999].
- Parameter:
- dataarray-like of shape (n_samples, n_features)
Die Datenmatrix mit p Merkmalen und n Stichproben. Der Datensatz muss derjenige sein, der zur Berechnung der rohen Schätzungen verwendet wurde.
- Gibt zurück:
- location_reweightedndarray von Form (n_features,)
Neu gewichtete robuste Lageschätzung.
- covariance_reweightedndarray von Form (n_features, n_features)
Neu gewichtete robuste Kovarianzschätzung.
- support_reweightedndarray von Form (n_samples,), dtype=bool
Eine Maske der Beobachtungen, die zur Berechnung der neu gewichteten robusten Lage- und Kovarianzschätzungen verwendet wurden.
Referenzen
[RVDriessen]A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
[Croux1999]Influence Function and Efficiency of the Minimum Covariance Determinant Scatter Matrix Estimator, 1999, Journal of Multivariate Analysis, Volume 71, Issue 2, Seiten 161-190
- score(X, y, sample_weight=None)[source]#
Gibt die durchschnittliche Genauigkeit auf den gegebenen Testdaten und Labels zurück.
Bei der Multi-Label-Klassifizierung ist dies die Subset-Genauigkeit, eine strenge Metrik, da für jede Stichprobe verlangt wird, dass jede Label-Menge korrekt vorhergesagt wird.
- Parameter:
- Xarray-like der Form (n_samples, n_features)
Teststichproben.
- yarray-like der Form (n_samples,) oder (n_samples, n_outputs)
Wahre Labels für X.
- sample_weightarray-like der Form (n_samples,), Standardwert=None
Stichprobengewichte.
- Gibt zurück:
- scorefloat
Mittlere Genauigkeit von self.predict(X) in Bezug auf y.
- score_samples(X)[source]#
Berechnet die negativen Mahalanobis-Distanzen.
- Parameter:
- Xarray-like der Form (n_samples, n_features)
Die Datenmatrix.
- Gibt zurück:
- negative_mahal_distancesarray-like von Form (n_samples,)
Gegenteil der Mahalanobis-Distanzen.
- set_params(**params)[source]#
Setzt die Parameter dieses Schätzers.
Die Methode funktioniert sowohl bei einfachen Schätzern als auch bei verschachtelten Objekten (wie
Pipeline). Letztere haben Parameter der Form<component>__<parameter>, so dass es möglich ist, jede Komponente eines verschachtelten Objekts zu aktualisieren.- Parameter:
- **paramsdict
Schätzer-Parameter.
- Gibt zurück:
- selfestimator instance
Schätzer-Instanz.
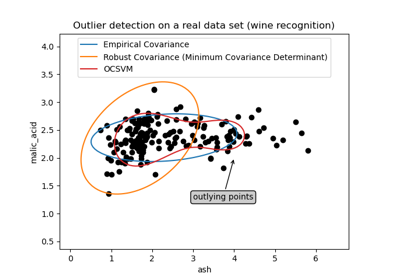
Galeriebeispiele#
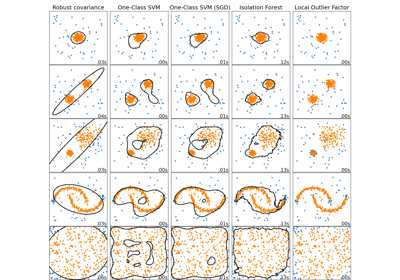
Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Toy-Datensätzen