v_measure_score#
- sklearn.metrics.v_measure_score(labels_true, labels_pred, *, beta=1.0)[Quelle]#
V-Measure Cluster-Beschriftung gegeben eine Grundwahrheit.
Diese Punktzahl ist identisch mit
normalized_mutual_info_scoremit der Option'arithmetic'für die Mittelwertbildung.Das V-Maß ist das harmonische Mittel zwischen Homogenität und Vollständigkeit
v = (1 + beta) * homogeneity * completeness / (beta * homogeneity + completeness)
Diese Metrik ist unabhängig von den absoluten Werten der Labels: eine Permutation der Klassen- oder Cluster-Labelwerte ändert den Score-Wert in keiner Weise.
Diese Metrik ist außerdem symmetrisch: das Vertauschen von
label_truemitlabel_predgibt denselben Punktwert zurück. Dies kann nützlich sein, um die Übereinstimmung zweier unabhängiger Label-Zuweisungsstrategien auf demselben Datensatz zu messen, wenn die tatsächliche Grundwahrheit nicht bekannt ist.Lesen Sie mehr im Benutzerhandbuch.
- Parameter:
- labels_truearray-like von Form (n_samples,)
Wahre Klassenlabels als Referenz.
- labels_predarray-like von Form (n_samples,)
Zu bewertende Clusterlabels.
- betafloat, Standard=1.0
Verhältnis des Gewichts, das
HomogenitätgegenüberVollständigkeitzugewiesen wird. Wennbetagrößer als 1 ist, wirdVollständigkeitbei der Berechnung stärker gewichtet. Wennbetakleiner als 1 ist, wirdHomogenitätstärker gewichtet.
- Gibt zurück:
- v_measurefloat
Score zwischen 0.0 und 1.0. 1.0 steht für eine perfekt vollständige Kennzeichnung.
Siehe auch
homogeneity_scoreHomogenitätsmetrik der Cluster-Kennzeichnung.
completeness_scoreVollständigkeitsmetrik der Cluster-Beschriftung.
normalized_mutual_info_scoreNormalisierte gegenseitige Information.
Referenzen
Beispiele
Perfekte Labellings sind sowohl homogen als auch vollständig, daher haben sie einen Score von 1,0
>>> from sklearn.metrics.cluster import v_measure_score >>> v_measure_score([0, 0, 1, 1], [0, 0, 1, 1]) 1.0 >>> v_measure_score([0, 0, 1, 1], [1, 1, 0, 0]) 1.0
Beschriftungen, die allen Klassenmitgliedern dieselben Cluster zuweisen, sind vollständig, aber nicht homogen und werden daher bestraft.
>>> print("%.6f" % v_measure_score([0, 0, 1, 2], [0, 0, 1, 1])) 0.8 >>> print("%.6f" % v_measure_score([0, 1, 2, 3], [0, 0, 1, 1])) 0.67
Beschriftungen, die reine Cluster mit Mitgliedern aus denselben Klassen haben, sind homogen, aber unnötige Aufteilungen beeinträchtigen die Vollständigkeit und werden daher auch für das V-Maß bestraft.
>>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 0, 1, 2])) 0.8 >>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 1, 2, 3])) 0.67
Wenn Klassenmitglieder vollständig über verschiedene Cluster verteilt sind, ist die Zuweisung völlig unvollständig, daher ist das V-Maß null.
>>> print("%.6f" % v_measure_score([0, 0, 0, 0], [0, 1, 2, 3])) 0.0
Cluster, die Stichproben aus völlig unterschiedlichen Klassen enthalten, zerstören die Homogenität der Beschriftung vollständig, daher
>>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 0, 0, 0])) 0.0
Galeriebeispiele#

Biclustering von Dokumenten mit dem Spectral Co-Clustering Algorithmus
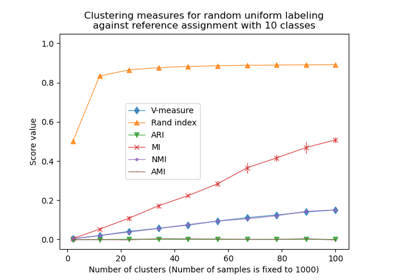
Anpassung für Zufälligkeit in der Clusterleistungsbewertung
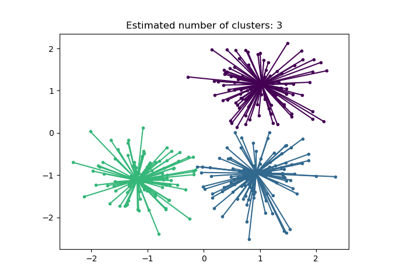
Demo des Affinity Propagation Clustering Algorithmus
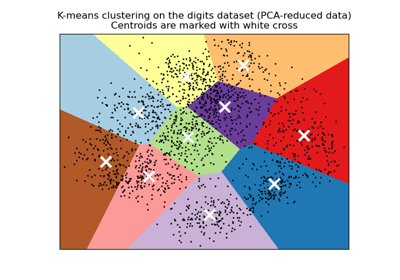
Eine Demo des K-Means Clusterings auf den handschriftlichen Zifferndaten