2.3. Clustering

Clustering von unbeschrifteten Daten kann mit dem Modul sklearn.cluster durchgeführt werden.

Jeder Clustering-Algorithmus hat zwei Varianten: eine Klasse, die die fit Methode implementiert, um die Cluster aus Trainingsdaten zu lernen, und eine Funktion, die, gegeben Trainingsdaten, ein Array von Ganzzahl-Labels zurückgibt, die den verschiedenen Clustern entsprechen. Für die Klasse sind die Labels der Trainingsdaten im Attribut labels_ zu finden.

Eingabedaten

Eine wichtige Anmerkung ist, dass die in diesem Modul implementierten Algorithmen verschiedene Arten von Matrizen als Eingabe akzeptieren können. Alle Methoden akzeptieren Standard-Datenmatrizen der Form (n_samples, n_features). Diese können aus den Klassen des Moduls sklearn.feature_extraction gewonnen werden. Für AffinityPropagation, SpectralClustering und DBSCAN kann auch eine Ähnlichkeitsmatrix der Form (n_samples, n_samples) als Eingabe verwendet werden. Diese können aus den Funktionen des Moduls sklearn.metrics.pairwise gewonnen werden.

2.3.1. Übersicht der Clustering-Methoden

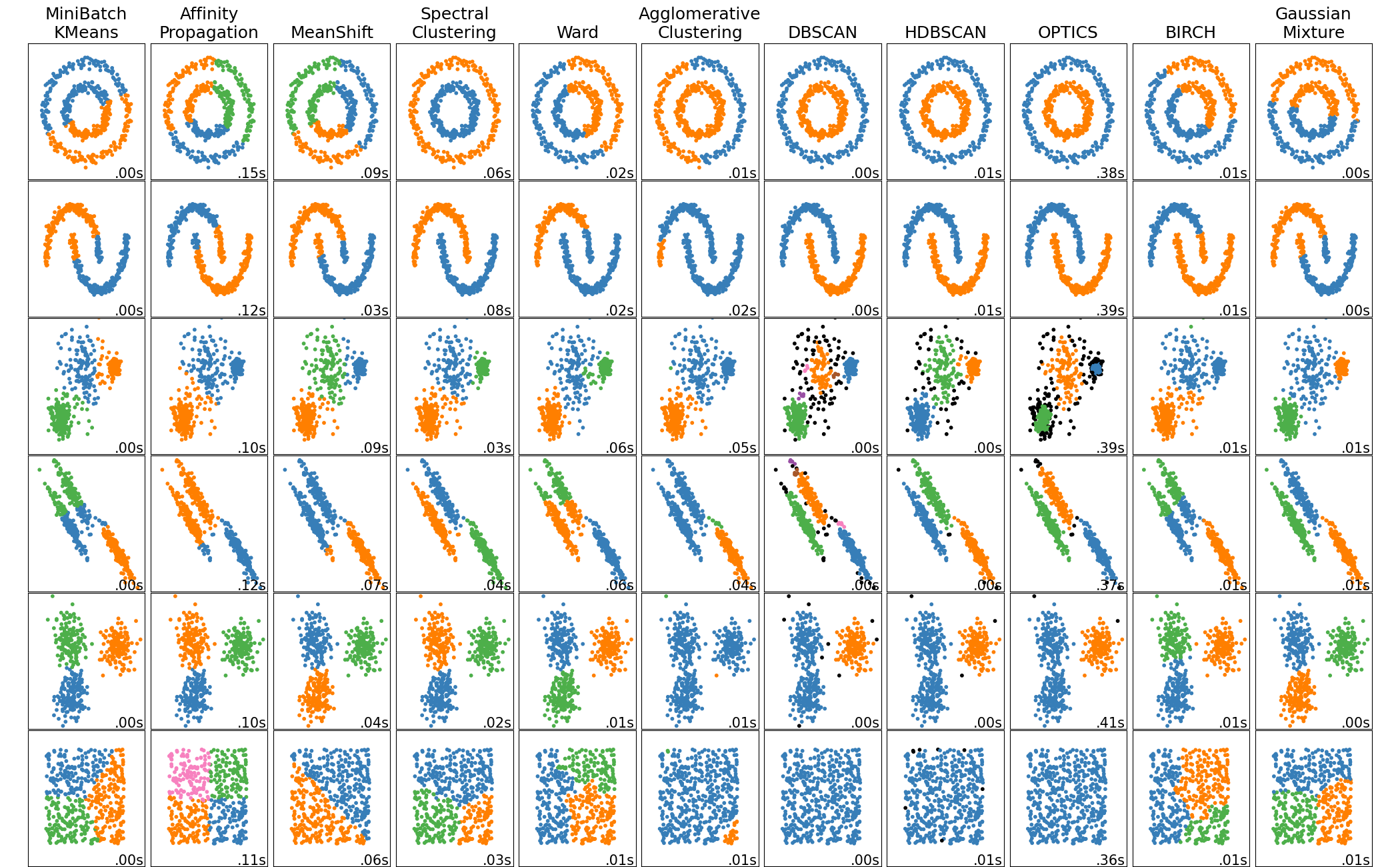
Ein Vergleich der Clustering-Algorithmen in scikit-learn

Methodenname	Parameter	Skalierbarkeit	Anwendungsfall	Geometrie (verwendete Metrik)
K-Means	Anzahl der Cluster	Sehr große n_samples, mittlere n_clusters mit MiniBatch-Code	Allgemein verwendbar, gleichmäßige Clustergröße, flache Geometrie, nicht zu viele Cluster, induktiv	Abstände zwischen Punkten
Affinity Propagation	Dämpfung, Sample-Präferenz	Nicht skalierbar mit n_samples	Viele Cluster, ungleichmäßige Clustergröße, nicht-flache Geometrie, induktiv	Graph-Abstand (z.B. Nearest-Neighbor-Graph)
Mean-Shift	Bandbreite	Nicht skalierbar mit n_samples	Viele Cluster, ungleichmäßige Clustergröße, nicht-flache Geometrie, induktiv	Abstände zwischen Punkten
Spektrales Clustering	Anzahl der Cluster	Mittlere n_samples, kleine n_clusters	Wenige Cluster, gleichmäßige Clustergröße, nicht-flache Geometrie, transduktiv	Graph-Abstand (z.B. Nearest-Neighbor-Graph)
Ward-Hierarchisches Clustering	Anzahl der Cluster oder Abstandsschwelle	Große n_samples und n_clusters	Viele Cluster, möglicherweise Konnektivitätsbeschränkungen, transduktiv	Abstände zwischen Punkten
Agglomeratives Clustering	Anzahl der Cluster oder Abstandsschwelle, Linkage-Typ, Abstand	Große n_samples und n_clusters	Viele Cluster, möglicherweise Konnektivitätsbeschränkungen, nicht-euklidische Abstände, transduktiv	Beliebiger paarweiser Abstand
DBSCAN	Nachbarschaftsgröße	Sehr große n_samples, mittlere n_clusters	Nicht-flache Geometrie, ungleichmäßige Clustergrößen, Ausreißerentfernung, transduktiv	Abstände zwischen nächsten Punkten
HDBSCAN	Minimale Clusterzugehörigkeit, minimale Punktnachbarn	Große n_samples, mittlere n_clusters	Nicht-flache Geometrie, ungleichmäßige Clustergrößen, variable Clusterdichte, Ausreißerentfernung, transduktiv, hierarchisch, variable Clusterdichte	Abstände zwischen nächsten Punkten
OPTICS	Minimale Clusterzugehörigkeit	Sehr große n_samples, große n_clusters	Nicht-flache Geometrie, ungleichmäßige Clustergrößen, variable Clusterdichte, Ausreißerentfernung, transduktiv	Abstände zwischen Punkten
Gaußsche Mischmodelle	Viele	Nicht skalierbar	Flache Geometrie, gut für Dichteschätzung, induktiv	Mahalanobis-Abstände zu Zentren
BIRCH	Verzweigungsfaktor, Schwelle, optionaler globaler Clusterer.	Große n_clusters und n_samples	Großer Datensatz, Ausreißerentfernung, Datenreduktion, induktiv	Euklidischer Abstand zwischen Punkten
Bisecting K-Means	Anzahl der Cluster	Sehr große n_samples, mittlere n_clusters	Allgemein verwendbar, gleichmäßige Clustergröße, flache Geometrie, keine leeren Cluster, induktiv, hierarchisch	Abstände zwischen Punkten

Nicht-flache Geometrie-Clustering ist nützlich, wenn die Cluster eine spezifische Form haben, d.h. eine nicht-flache Mannigfaltigkeit, und der Standard-Euklidische Abstand nicht die richtige Metrik ist. Dies tritt in den beiden oberen Zeilen der obigen Abbildung auf.

Gaußsche Mischmodelle, nützlich für Clustering, werden in einem anderen Kapitel der Dokumentation beschrieben, das sich mit Mischmodellen befasst. KMeans kann als Spezialfall eines Gaußschen Mischmodells mit gleicher Kovarianz pro Komponente betrachtet werden.

Transduktive Clustering-Methoden (im Gegensatz zu induktiven Clustering-Methoden) sind nicht darauf ausgelegt, auf neue, ungesehene Daten angewendet zu werden.

Beispiele

• Induktives Clustering: Ein Beispiel für ein induktives Clustering-Modell zur Verarbeitung neuer Daten.

2.3.2. K-Means

Der KMeans-Algorithmus clustert Daten, indem er versucht, Stichproben in n Gruppen gleicher Varianz zu trennen, und dabei ein Kriterium minimiert, das als Inertia oder Within-Cluster-Sum-of-Squares (siehe unten) bekannt ist. Dieser Algorithmus erfordert die Angabe der Anzahl der Cluster. Er skaliert gut mit einer großen Anzahl von Stichproben und wurde in einer Vielzahl von Anwendungsbereichen in vielen verschiedenen Feldern eingesetzt.

Der K-Means-Algorithmus teilt eine Menge von \(N\) Stichproben \(X\) in \(K\) disjunkte Cluster \(C\) auf, die jeweils durch den Mittelwert \(\mu_j\) der Stichproben im Cluster beschrieben werden. Die Mittelwerte werden üblicherweise als Cluster-"Zentroiden" bezeichnet; beachten Sie, dass dies im Allgemeinen keine Punkte aus \(X\) sind, obwohl sie im selben Raum liegen.

Der K-Means-Algorithmus zielt darauf ab, Zentroiden zu wählen, die die **Inertia** oder das **Kriterium der Within-Cluster-Sum-of-Squares** minimieren.

\[\sum_{i=0}^{n}\min_{\mu_j \in C}(||x_i - \mu_j||^2)\]

Inertia kann als Maß dafür erkannt werden, wie kohärent die Cluster intern sind. Sie hat verschiedene Nachteile.

• Inertia geht von konvexen und isotropen Clustern aus, was nicht immer der Fall ist. Sie reagiert schlecht auf gestreckte Cluster oder Mannigfaltigkeiten mit unregelmäßigen Formen.

• Inertia ist keine normalisierte Metrik: Wir wissen nur, dass niedrigere Werte besser sind und Null optimal ist. Aber in sehr hochdimensionalen Räumen tendieren Euklidische Abstände dazu, sich aufzublähen (dies ist eine Instanz des sogenannten "Fluchs der Dimensionalität"). Die Anwendung eines Dimensionsreduktionsalgorithmus wie der Principal Component Analysis (PCA) vor dem K-Means-Clustering kann dieses Problem lindern und die Berechnungen beschleunigen.

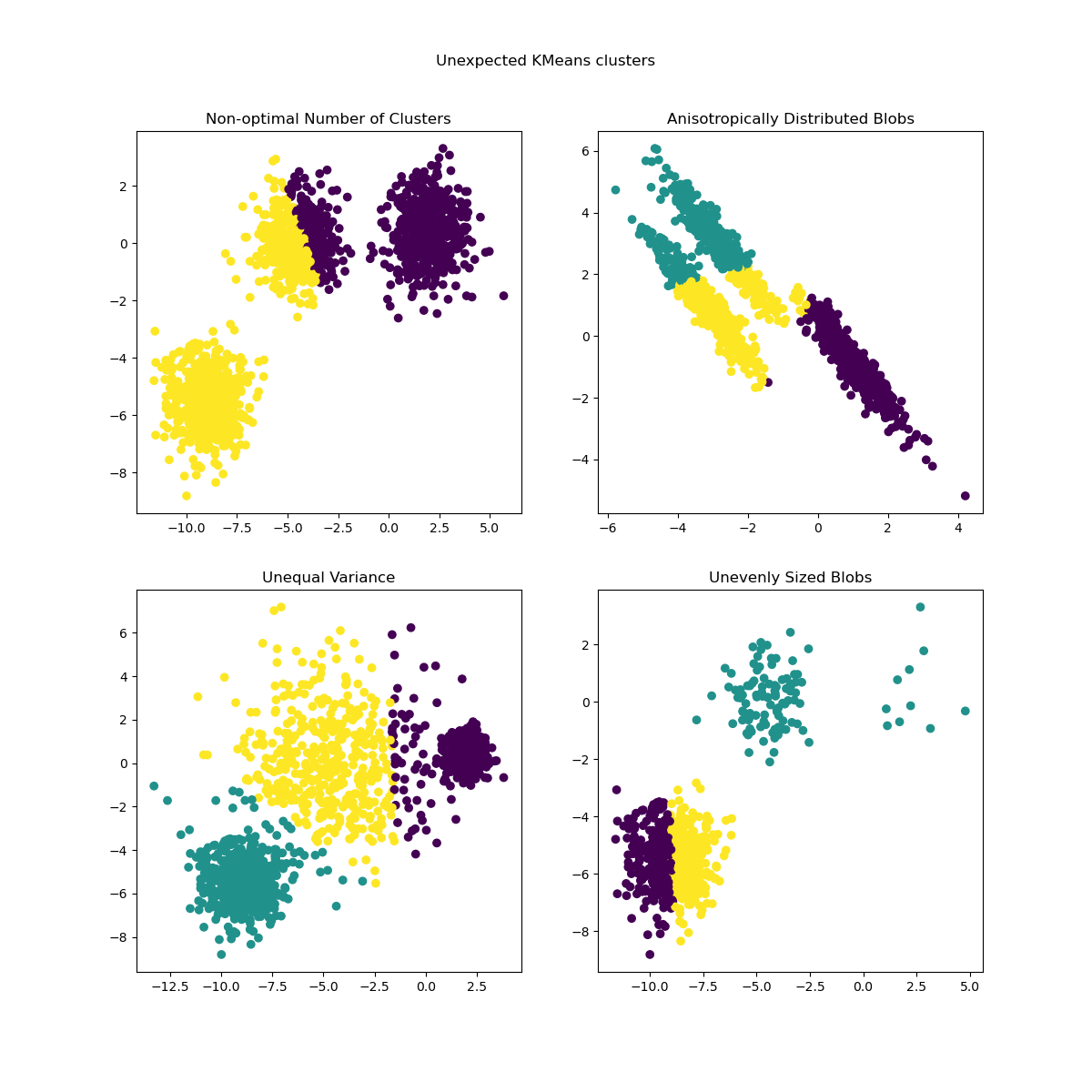
Für detailliertere Beschreibungen der oben genannten Probleme und wie sie behoben werden können, siehe die Beispiele Demonstration von K-Means-Annahmen und Auswahl der Anzahl von Clustern mit Silhouettenanalyse auf KMeans-Clustering.

K-Means wird oft als Lloyd-Algorithmus bezeichnet. Grundsätzlich besteht der Algorithmus aus drei Schritten. Der erste Schritt wählt die anfänglichen Zentroiden, wobei die einfachste Methode darin besteht, \(k\) Stichproben aus dem Datensatz \(X\) zu wählen. Nach der Initialisierung besteht K-Means darin, zwischen den beiden anderen Schritten zu iterieren. Der erste Schritt weist jede Stichprobe ihrem nächsten Zentroiden zu. Der zweite Schritt erstellt neue Zentroiden, indem der Mittelwert aller Stichproben, die jedem vorherigen Zentroiden zugewiesen wurden, berechnet wird. Die Differenz zwischen den alten und den neuen Zentroiden wird berechnet, und der Algorithmus wiederholt diese letzten beiden Schritte, bis dieser Wert kleiner als ein Schwellenwert ist. Mit anderen Worten, er wiederholt sich, bis sich die Zentroiden nicht mehr signifikant bewegen.

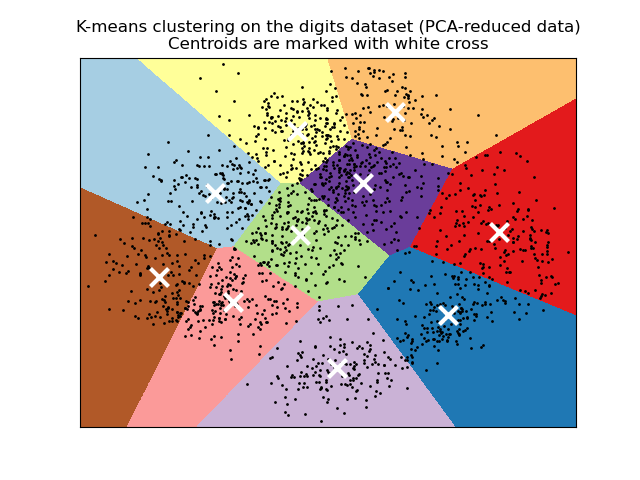
K-Means ist äquivalent zum Erwartungsmaximierungsalgorithmus mit einer kleinen, alles gleichen, diagonalen Kovarianzmatrix.

Der Algorithmus kann auch durch das Konzept der Voronoi-Diagramme verstanden werden. Zuerst wird das Voronoi-Diagramm der Punkte mit den aktuellen Zentroiden berechnet. Jedes Segment im Voronoi-Diagramm wird zu einem separaten Cluster. Zweitens werden die Zentroiden auf den Mittelwert jedes Segments aktualisiert. Der Algorithmus wiederholt dies dann, bis ein Abbruchkriterium erfüllt ist. Normalerweise stoppt der Algorithmus, wenn die relative Abnahme der Zielfunktion zwischen den Iterationen kleiner ist als der angegebene Toleranzwert. Dies ist in dieser Implementierung nicht der Fall: Die Iteration stoppt, wenn sich die Zentroiden weniger als die Toleranz bewegen.

Bei genügend Zeit konvergiert K-Means immer, allerdings kann dies zu einem lokalen Minimum führen. Dies hängt stark von der Initialisierung der Zentroiden ab. Daher wird die Berechnung oft mehrmals mit unterschiedlichen Initialisierungen der Zentroiden durchgeführt. Eine Methode zur Bewältigung dieses Problems ist das K-Means++-Initialisierungsschema, das in scikit-learn implementiert ist (verwenden Sie den Parameter init='k-means++'). Dies initialisiert die Zentroiden so, dass sie (im Allgemeinen) weit voneinander entfernt sind, was wahrscheinlich zu besseren Ergebnissen als die zufällige Initialisierung führt, wie in der Referenz gezeigt. Detaillierte Beispiele für den Vergleich verschiedener Initialisierungsschemata finden Sie unter Eine Demo von K-Means-Clustering auf den handschriftlichen Zifferndaten und Empirische Bewertung des Einflusses der K-Means-Initialisierung.

K-Means++ kann auch unabhängig aufgerufen werden, um Seeds für andere Clustering-Algorithmen auszuwählen. Siehe sklearn.cluster.kmeans_plusplus für Details und Anwendungsbeispiele.

Der Algorithmus unterstützt Stichprobengewichte, die über einen Parameter sample_weight übergeben werden können. Dies ermöglicht es, einigen Stichproben mehr Gewicht bei der Berechnung von Clusterzentren und Inertia-Werten zu geben. Beispielsweise ist die Zuweisung eines Gewichts von 2 zu einer Stichprobe gleichbedeutend mit dem Hinzufügen einer Duplikats dieser Stichprobe zum Datensatz \(X\).

Beispiele

• Clustering von Textdokumenten mit K-Means: Dokumentenclustering mit KMeans und MiniBatchKMeans auf Basis von spärlichen Daten

• Ein Beispiel für K-Means++-Initialisierung: Verwendung von K-Means++ zur Auswahl von Seeds für andere Clustering-Algorithmen.

2.3.2.1. Low-Level-Parallelität

KMeans profitiert von OpenMP-basierter Parallelität durch Cython. Kleine Datenabschnitte (256 Stichproben) werden parallel verarbeitet, was zusätzlich einen geringen Speicherbedarf ergibt. Weitere Details zur Steuerung der Anzahl der Threads finden Sie in unseren Hinweisen zur Parallelität.

Beispiele

• Demonstration von K-Means-Annahmen: Demonstration, wann K-Means intuitiv funktioniert und wann nicht.

• Eine Demo von K-Means-Clustering auf den handschriftlichen Zifferndaten: Clustering von handschriftlichen Ziffern.

Referenzen

• „k-means++: The advantages of careful seeding“ Arthur, David, und Sergei Vassilvitskii, Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, Society for Industrial and Applied Mathematics (2007)

2.3.2.2. Mini Batch K-Means

Die MiniBatchKMeans ist eine Variante des KMeans-Algorithmus, der Mini-Batches verwendet, um die Berechnungszeit zu verkürzen, während er dennoch versucht, dieselbe Zielfunktion zu optimieren. Mini-Batches sind Teilmengen der Eingabedaten, die in jeder Trainingsiteration zufällig gezogen werden. Diese Mini-Batches reduzieren drastisch die Menge der erforderlichen Berechnungen, um zu einer lokalen Lösung zu konvergieren. Im Gegensatz zu anderen Algorithmen, die die Konvergenzzeit von K-Means reduzieren, liefert Mini-Batch-K-Means Ergebnisse, die im Allgemeinen nur geringfügig schlechter sind als die des Standardalgorithmus.

Der Algorithmus iteriert zwischen zwei Hauptschritten, ähnlich dem Vanilla K-Means. Im ersten Schritt werden \(b\) Stichproben zufällig aus dem Datensatz gezogen, um einen Mini-Batch zu bilden. Diese werden dann dem nächstgelegenen Zentroiden zugewiesen. Im zweiten Schritt werden die Zentroiden aktualisiert. Im Gegensatz zu K-Means geschieht dies auf Stichprobenbasis. Für jede Stichprobe im Mini-Batch wird der zugewiesene Zentroid durch die Streaming-Mittelung der Stichprobe und aller vorherigen Stichproben, die diesem Zentroiden zugewiesen wurden, aktualisiert. Dies hat den Effekt, die Änderungsrate eines Zentroiden im Laufe der Zeit zu verringern. Diese Schritte werden bis zur Konvergenz oder bis zum Erreichen einer vordefinierten Anzahl von Iterationen durchgeführt.

MiniBatchKMeans konvergiert schneller als KMeans, aber die Qualität der Ergebnisse ist reduziert. In der Praxis kann dieser Qualitätsunterschied recht gering sein, wie im Beispiel und in der zitierten Referenz gezeigt.

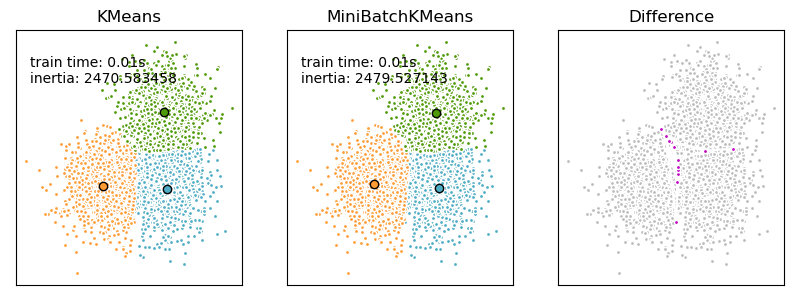
Beispiele

• Vergleich der K-Means- und MiniBatchKMeans-Clustering-Algorithmen: Vergleich von KMeans und MiniBatchKMeans.

• Clustering von Textdokumenten mit K-Means: Dokumentenclustering mit KMeans und MiniBatchKMeans auf Basis von spärlichen Daten

• Online-Lernen eines Diktionärs von Gesichtsteilen

Referenzen

• „Web Scale K-Means clustering“ D. Sculley, Proceedings of the 19th international conference on World wide web (2010).

2.3.3. Affinity Propagation

AffinityPropagation erstellt Cluster, indem es Nachrichten zwischen Stichprobenpaaren sendet, bis Konvergenz erreicht ist. Ein Datensatz wird dann anhand einer kleinen Anzahl von Exemplaren beschrieben, die als die repräsentativsten für andere Stichproben identifiziert werden. Die zwischen Paaren gesendeten Nachrichten repräsentieren die Eignung eines Stichproben, das Exemplar eines anderen zu sein, was in Reaktion auf die Werte anderer Paare aktualisiert wird. Diese Aktualisierung geschieht iterativ bis zur Konvergenz, an welchem Punkt die endgültigen Exemplare gewählt werden und somit das endgültige Clustering gegeben ist.

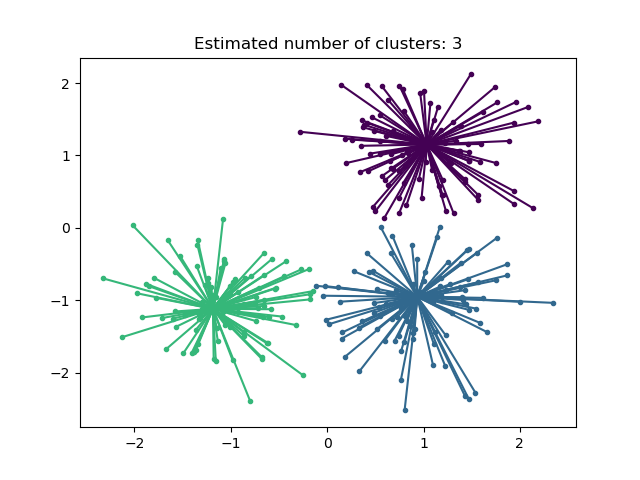
Affinity Propagation kann interessant sein, da es die Anzahl der Cluster basierend auf den bereitgestellten Daten wählt. Zu diesem Zweck sind die beiden wichtigen Parameter die Präferenz, die steuert, wie viele Exemplare verwendet werden, und der Dämpfungsfaktor, der die Verantwortungs- und Verfügbarkeitsnachrichten dämpft, um numerische Oszillationen bei der Aktualisierung dieser Nachrichten zu vermeiden.

Der Hauptnachteil von Affinity Propagation ist seine Komplexität. Der Algorithmus hat eine Zeitkomplexität der Ordnung \(O(N^2 T)\), wobei \(N\) die Anzahl der Stichproben und \(T\) die Anzahl der Iterationen bis zur Konvergenz ist. Darüber hinaus ist die Speicherkomplexität der Ordnung \(O(N^2)\), wenn eine dichte Ähnlichkeitsmatrix verwendet wird, kann aber bei Verwendung einer spärlichen Ähnlichkeitsmatrix reduziert werden. Dies macht Affinity Propagation am besten für kleine bis mittlere Datensätze geeignet.

Algorithmenbeschreibung

Die zwischen den Punkten gesendeten Nachrichten gehören einer von zwei Kategorien an. Die erste ist die Verantwortung \(r(i, k)\), die die gesammelte Evidenz dafür ist, dass Stichprobe \(k\) das Exemplar für Stichprobe \(i\) sein sollte. Die zweite ist die Verfügbarkeit \(a(i, k)\), die die gesammelte Evidenz dafür ist, dass Stichprobe \(i\) Stichprobe \(k\) als ihr Exemplar wählen sollte, und die Werte aller anderen Stichproben berücksichtigt, für die \(k\) ein Exemplar sein sollte. Auf diese Weise werden Exemplare von Stichproben gewählt, wenn sie (1) ähnlich genug zu vielen Stichproben sind und (2) von vielen Stichproben als repräsentativ für sich selbst gewählt werden.

Formaler ausgedrückt, die Verantwortung einer Stichprobe \(k\), das Exemplar von Stichprobe \(i\) zu sein, ist gegeben durch

\[r(i, k) \leftarrow s(i, k) - max [ a(i, k') + s(i, k') \forall k' \neq k ]\]

Wobei \(s(i, k)\) die Ähnlichkeit zwischen den Stichproben \(i\) und \(k\) ist. Die Verfügbarkeit von Stichprobe \(k\), das Exemplar von Stichprobe \(i\) zu sein, ist gegeben durch

\[a(i, k) \leftarrow min [0, r(k, k) + \sum_{i'~s.t.~i' \notin \{i, k\}}{r(i', k)}]\]

Zu Beginn werden alle Werte für \(r\) und \(a\) auf Null gesetzt, und die Berechnung jeder Iteration erfolgt bis zur Konvergenz. Wie oben erwähnt, wird zur Vermeidung numerischer Oszillationen bei der Aktualisierung der Nachrichten der Dämpfungsfaktor \(\lambda\) in den Iterationsprozess eingeführt.

\[r_{t+1}(i, k) = \lambda\cdot r_{t}(i, k) + (1-\lambda)\cdot r_{t+1}(i, k)\]

\[a_{t+1}(i, k) = \lambda\cdot a_{t}(i, k) + (1-\lambda)\cdot a_{t+1}(i, k)\]

wobei \(t\) die Iterationszeit angibt.

Beispiele

• Demo des Affinity Propagation Clustering-Algorithmus: Affinity Propagation auf synthetischen 2D-Datensätzen mit 3 Klassen.

• Visualisierung der Aktienmarktstruktur Affinity Propagation auf Finanzzeitreihen zur Identifizierung von Unternehmensgruppen.

2.3.4. Mean Shift

MeanShift Clustering zielt darauf ab, Blobs in einer glatten Dichte von Stichproben zu entdecken. Es ist ein zentroidbasierter Algorithmus, der funktioniert, indem er Kandidaten für Zentroiden zum Mittelwert der Punkte innerhalb einer gegebenen Region aktualisiert. Diese Kandidaten werden dann in einer Nachbearbeitungsphase gefiltert, um nahe Duplikate zu eliminieren und die endgültige Menge an Zentroiden zu bilden.

Mathematische Details

Die Position von Zentroidenkandidaten wird iterativ mithilfe einer Technik namens Hill Climbing angepasst, die lokale Maxima der geschätzten Wahrscheinlichkeitsdichte findet. Gegeben ein Kandidaten-Zentroid \(x\) für die Iteration \(t\), wird der Kandidat gemäß der folgenden Gleichung aktualisiert:

\[x^{t+1} = x^t + m(x^t)\]

Wobei \(m\) der Mean Shift-Vektor ist, der für jeden Zentroiden berechnet wird und auf eine Region des maximalen Anstiegs der Punktdichte hinweist. Um \(m\) zu berechnen, definieren wir \(N(x)\) als die Nachbarschaft von Stichproben innerhalb eines gegebenen Abstands um \(x\). Dann wird \(m\) mit der folgenden Gleichung berechnet, die effektiv einen Zentroiden zum Mittelwert der Stichproben in seiner Nachbarschaft aktualisiert:

\[m(x) = \frac{1}{|N(x)|} \sum_{x_j \in N(x)}x_j - x\]

Im Allgemeinen hängt die Gleichung für \(m\) von einem Kernel ab, der zur Dichteschätzung verwendet wird. Die allgemeine Formel lautet:

\[m(x) = \frac{\sum_{x_j \in N(x)}K(x_j - x)x_j}{\sum_{x_j \in N(x)}K(x_j - x)} - x\]

In unserer Implementierung ist \(K(x)\) gleich 1, wenn \(x\) klein genug ist, und andernfalls gleich 0. Effektiv gibt \(K(y - x)\) an, ob \(y\) in der Nachbarschaft von \(x\) liegt.

Der Algorithmus legt die Anzahl der Cluster automatisch fest, anstatt sich auf einen Parameter bandwidth zu verlassen, der die Größe der zu durchsuchenden Region bestimmt. Dieser Parameter kann manuell eingestellt werden, kann aber mithilfe der bereitgestellten Funktion estimate_bandwidth geschätzt werden, die aufgerufen wird, wenn die Bandbreite nicht eingestellt ist.

Der Algorithmus ist nicht sehr skalierbar, da er während der Ausführung des Algorithmus mehrere Suchen nach nächstgelegenen Nachbarn erfordert. Der Algorithmus konvergiert garantiert, jedoch stoppt der Algorithmus die Iteration, wenn die Änderung der Zentroiden gering ist.

Die Zuordnung eines neuen Stichproben erfolgt durch Finden des nächstgelegenen Zentroiden für eine gegebene Stichprobe.

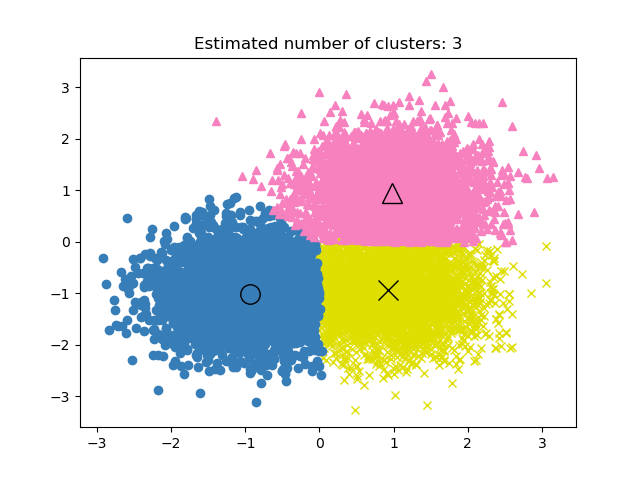
Beispiele

• Eine Demo des Mean-Shift-Clustering-Algorithmus: Mean Shift Clustering auf synthetischen 2D-Datensätzen mit 3 Klassen.

Referenzen

• „Mean shift: A robust approach toward feature space analysis“ D. Comaniciu und P. Meer, IEEE Transactions on Pattern Analysis and Machine Intelligence (2002)

2.3.5. Spektrales Clustering

SpectralClustering führt eine niedrigdimensionale Einbettung der Ähnlichkeitsmatrix zwischen Stichproben durch, gefolgt von Clustering, z.B. mit KMeans, der Komponenten der Eigenvektoren im niedrigdimensionalen Raum. Dies ist besonders rechnerisch effizient, wenn die Ähnlichkeitsmatrix spärlich ist und der amg-Solver für das Eigenwertproblem verwendet wird (Hinweis: Der amg-Solver erfordert, dass das Modul pyamg installiert ist).

Die vorliegende Version von SpectralClustering erfordert die vorherige Angabe der Anzahl der Cluster. Sie funktioniert gut für eine kleine Anzahl von Clustern, ist aber für viele Cluster nicht ratsam.

Für zwei Cluster löst SpectralClustering eine konvexe Relaxation des Problems der normalisierten Schnitte im Ähnlichkeitsgraphen: den Graphen in zwei Teile schneiden, so dass die Gewichtung der geschnittenen Kanten im Vergleich zu den Gewichtungen der Kanten innerhalb jedes Clusters gering ist. Dieses Kriterium ist besonders interessant bei der Arbeit mit Bildern, bei denen die Graphenknoten Pixel sind und die Gewichtungen der Kanten des Ähnlichkeitsgraphen mithilfe einer Funktion des Bildgradienten berechnet werden.

Warnung

Umwandlung von Abständen in gut funktionierende Ähnlichkeiten

Beachten Sie, dass das spektrale Problem singulär und somit nicht lösbar ist, wenn die Werte Ihrer Ähnlichkeitsmatrix nicht gut verteilt sind, z. B. mit negativen Werten oder mit einer Distanzmatrix anstelle einer Ähnlichkeitsmatrix. In diesem Fall empfiehlt es sich, die Einträge der Matrix zu transformieren. Beispielsweise wird im Falle einer vorzeichenbehafteten Distanzmatrix häufig ein Heat Kernel angewendet.

similarity = np.exp(-beta * distance / distance.std())

Siehe die Beispiele für eine solche Anwendung.

Beispiele

• Spektrales Clustering für die Bildsegmentierung: Segmentierung von Objekten aus einem verrauschten Hintergrund mittels spektralem Clustering.

• Segmentierung des Bildes griechischer Münzen in Regionen: Spektrales Clustering zur Aufteilung des Münzbildes in Regionen.

2.3.5.1. Verschiedene Strategien zur Zuweisung von Labels

Es können verschiedene Strategien zur Zuweisung von Labels verwendet werden, die dem Parameter assign_labels von SpectralClustering entsprechen. Die Strategie "kmeans" kann feinere Details erfassen, ist aber instabil. Insbesondere, es sei denn, Sie kontrollieren den random_state, kann sie von Lauf zu Lauf nicht reproduzierbar sein, da sie von einer zufälligen Initialisierung abhängt. Die alternative Strategie "discretize" ist zu 100 % reproduzierbar, tendiert aber dazu, Parzellen von recht gleichmäßiger und geometrischer Form zu erzeugen. Die kürzlich hinzugefügte Option "cluster_qr" ist eine deterministische Alternative, die in der untenstehenden Anwendungsübersicht visuell die beste Partitionierung erzeugt.

assign_labels="kmeans"	assign_labels="discretize"	assign_labels="cluster_qr"

Referenzen

• „Multiclass spectral clustering“ Stella X. Yu, Jianbo Shi, 2003

• „Simple, direct, and efficient multi-way spectral clustering“ Anil Damle, Victor Minden, Lexing Ying, 2019

2.3.5.2. Spektrale Clustering-Graphen

Spektrales Clustering kann auch zur Partitionierung von Graphen über deren spektrale Einbettungen verwendet werden. In diesem Fall ist die Ähnlichkeitsmatrix die Adjazenzmatrix des Graphen, und SpectralClustering wird mit affinity='precomputed' initialisiert.

>>> from sklearn.cluster import SpectralClustering
>>> sc = SpectralClustering(3, affinity='precomputed', n_init=100,
...                         assign_labels='discretize')
>>> sc.fit_predict(adjacency_matrix)

Referenzen

• „A Tutorial on Spectral Clustering“ Ulrike von Luxburg, 2007

• „Normalized cuts and image segmentation“ Jianbo Shi, Jitendra Malik, 2000

• „A Random Walks View of Spectral Segmentation“ Marina Meila, Jianbo Shi, 2001

• „On Spectral Clustering: Analysis and an algorithm“ Andrew Y. Ng, Michael I. Jordan, Yair Weiss, 2001

• „Preconditioned Spectral Clustering for Stochastic Block Partition Streaming Graph Challenge“ David Zhuzhunashvili, Andrew Knyazev

2.3.6. Hierarchisches Clustering

Hierarchisches Clustering ist eine allgemeine Familie von Clustering-Algorithmen, die durch sukzessives Zusammenführen oder Aufteilen von Clustern verschachtelte Cluster aufbauen. Diese Hierarchie von Clustern wird als Baum (oder Dendrogramm) dargestellt. Die Wurzel des Baumes ist der eindeutige Cluster, der alle Stichproben sammelt, die Blätter sind die Cluster mit nur einer Stichprobe. Weitere Details finden Sie auf der Wikipedia-Seite.

Das Objekt AgglomerativeClustering führt ein hierarchisches Clustering mit einem Bottom-up-Ansatz durch: Jede Beobachtung beginnt in ihrem eigenen Cluster, und Cluster werden sukzessiv zusammengeführt. Das Verknüpfungskriterium bestimmt die Metrik, die für die Zusammenführungsstrategie verwendet wird.

• Ward minimiert die Summe der quadrierten Differenzen innerhalb aller Cluster. Es ist ein varianzminimierender Ansatz und ähnelt in diesem Sinne der Zielfunktion von k-Means, wird jedoch mit einem agglomerativen hierarchischen Ansatz angegangen.

• Maximum oder Complete Linkage minimiert den maximalen Abstand zwischen Beobachtungen von Cluster-Paaren.

• Average Linkage minimiert den Durchschnitt der Abstände zwischen allen Beobachtungen von Cluster-Paaren.

• Single Linkage minimiert den Abstand zwischen den nächsten Beobachtungen von Cluster-Paaren.

AgglomerativeClustering kann auch auf eine große Anzahl von Stichproben skaliert werden, wenn es zusammen mit einer Konnektivitätsmatrix verwendet wird, ist aber rechnerisch teuer, wenn keine Konnektivitätsbeschränkungen zwischen Stichproben hinzugefügt werden: Es werden bei jedem Schritt alle möglichen Zusammenführungen berücksichtigt.

FeatureAgglomeration

Die FeatureAgglomeration verwendet agglomeratives Clustering, um sehr ähnliche Merkmale zu gruppieren und somit die Anzahl der Merkmale zu reduzieren. Es ist ein Werkzeug zur Dimensionsreduktion, siehe Unüberwachte Dimensionsreduktion.

2.3.6.1. Verschiedene Verknüpfungsarten: Ward, Complete, Average und Single Linkage

AgglomerativeClustering unterstützt die Verknüpfungsstrategien Ward, Single, Average und Complete.

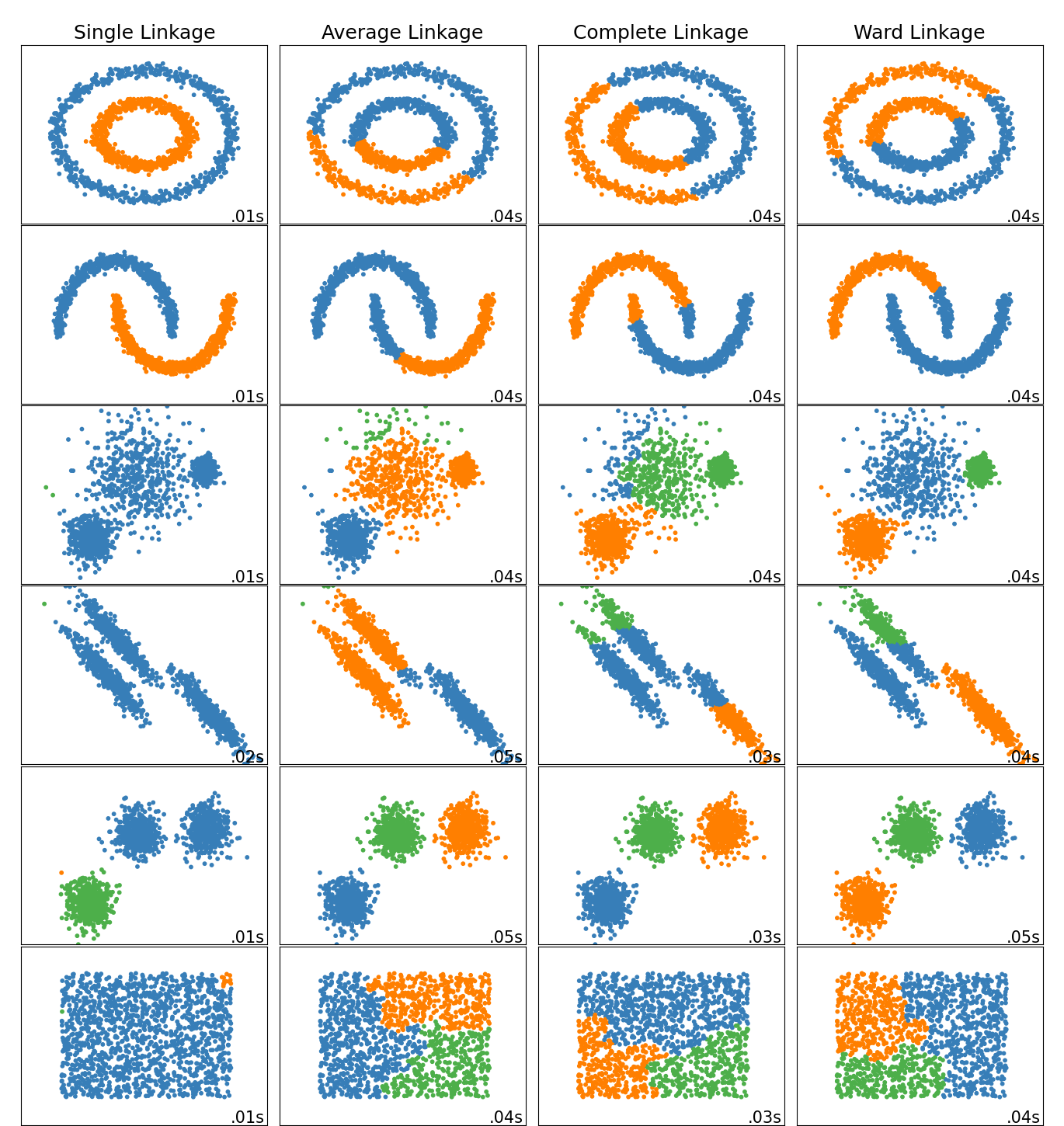
Agglomeratives Cluster hat ein "Reiche werden reicher"-Verhalten, das zu ungleichmäßigen Clustergrößen führt. In dieser Hinsicht ist Single Linkage die schlechteste Strategie, und Ward liefert die regelmäßigsten Größen. Die Affinität (oder Distanz, die beim Clustering verwendet wird) kann jedoch bei Ward nicht variiert werden, daher ist bei nicht-euklidischen Metriken Average Linkage eine gute Alternative. Single Linkage ist zwar nicht robust gegenüber verrauschten Daten, kann aber sehr effizient berechnet werden und ist daher nützlich, um hierarchische Cluster von größeren Datensätzen bereitzustellen. Single Linkage kann auch bei nicht-globulären Daten gut funktionieren.

Beispiele

• Verschiedene agglomerative Cluster auf einer 2D-Einbettung von Ziffern: Erkundung der verschiedenen Verknüpfungsstrategien in einem realen Datensatz.

  • Vergleich verschiedener hierarchischer Verknüpfungsmethoden auf Toy-Datensätzen: Erkundung der verschiedenen Verknüpfungsstrategien in Toy-Datensätzen.

2.3.6.2. Visualisierung der Clusterhierarchie

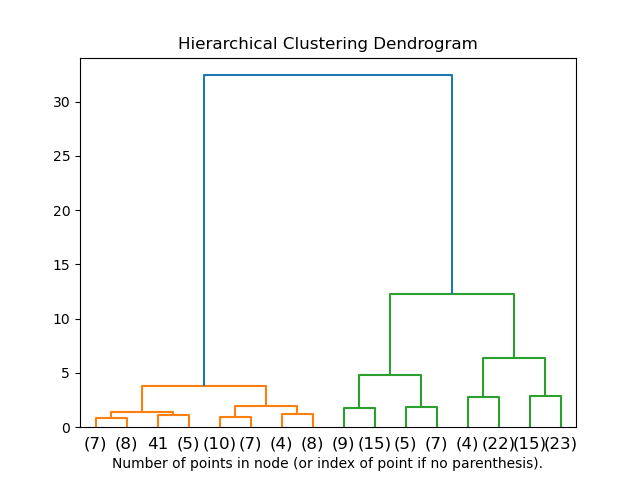
Es ist möglich, den Baum, der die hierarchische Zusammenführung von Clustern darstellt, als Dendrogramm zu visualisieren. Eine visuelle Inspektion kann oft nützlich sein, um die Struktur der Daten zu verstehen, insbesondere bei kleinen Stichprobengrößen.

Beispiele

• Hierarchisches Clustering Dendrogramm plotten

2.3.6.3. Hinzufügen von Konnektivitätsbeschränkungen

Ein interessanter Aspekt von AgglomerativeClustering ist, dass diesem Algorithmus Konnektivitätsbeschränkungen hinzugefügt werden können (nur benachbarte Cluster können zusammengeführt werden), über eine Konnektivitätsmatrix, die für jede Stichprobe die benachbarten Stichproben gemäß einer gegebenen Struktur der Daten definiert. Beispielsweise verbieten die Konnektivitätsbeschränkungen im untenstehenden Swiss-Roll-Beispiel die Zusammenführung von Punkten, die auf der Swiss Roll nicht benachbart sind, und verhindern so, dass sich Cluster über überlappende Falten der Rolle erstrecken.

Diese Beschränkungen sind nicht nur nützlich, um eine bestimmte lokale Struktur aufzuerlegen, sondern machen den Algorithmus auch schneller, insbesondere bei einer hohen Anzahl von Stichproben.

Die Konnektivitätsbeschränkungen werden über eine Konnektivitätsmatrix auferlegt: eine spärliche Scipy-Matrix, die nur an den Schnittstellen einer Zeile und einer Spalte mit Indizes des Datensatzes, die verbunden sein sollen, Einträge enthält. Diese Matrix kann aus a-priori-Informationen erstellt werden: Sie möchten beispielsweise Webseiten clusteren, indem Sie nur Seiten zusammenführen, auf die eine andere Seite verweist. Sie kann auch aus den Daten gelernt werden, zum Beispiel unter Verwendung von sklearn.neighbors.kneighbors_graph, um die Zusammenführung auf die nächsten Nachbarn zu beschränken, wie in diesem Beispiel, oder unter Verwendung von sklearn.feature_extraction.image.grid_to_graph, um nur die Zusammenführung von benachbarten Pixeln in einem Bild zu ermöglichen, wie im Münz-Beispiel.

Warnung

Konnektivitätsbeschränkungen mit Single, Average und Complete Linkage

Konnektivitätsbeschränkungen und Single-, Average- und Complete-Linkage können den Aspekt des "Reiche werden reicher" des agglomerativen Clusterings verstärken, insbesondere wenn sie mit sklearn.neighbors.kneighbors_graph erstellt werden. Im Grenzfall einer geringen Anzahl von Clustern tendieren sie dazu, einige makroskopisch besetzte Cluster und fast leere zu erzeugen. (Siehe die Diskussion in Hierarchisches Clustering mit und ohne Struktur). Single Linkage ist die am stärksten anfällige Verknüpfungsoption in Bezug auf dieses Problem.

Beispiele

• Eine Demo von strukturiertem Ward-Hierarchie-Clustering auf einem Bild von Münzen: Ward-Clustering zur Aufteilung des Münzbildes in Regionen.

• Hierarchisches Clustering mit und ohne Struktur: Beispiel für den Ward-Algorithmus auf einem Swiss-Roll, Vergleich von strukturierten Ansätzen und unstrukturierten Ansätzen.

• Feature-Agglomeration im Vergleich zur univariaten Auswahl: Beispiel für Dimensionsreduktion mit Feature-Agglomeration basierend auf Ward-Hierarchie-Clustering.

2.3.6.4. Variieren der Metrik

Single-, Average- und Complete-Linkage können mit einer Vielzahl von Abständen (oder Affinitäten) verwendet werden, insbesondere mit der euklidischen Distanz (l2), der Manhattan-Distanz (oder Cityblock, oder l1), der Kosinus-Distanz oder einer beliebigen vordefinierten Affinitätsmatrix.

• Die l1-Distanz ist oft gut für spärliche Merkmale oder spärliches Rauschen geeignet: d. h. viele der Merkmale sind Null, wie im Text-Mining bei der Verwendung von Vorkommen seltener Wörter.

• Die Kosinus-Distanz ist interessant, da sie invariant gegenüber globalen Skalierungen des Signals ist.

Die Richtlinien für die Wahl einer Metrik lauten, eine zu verwenden, die den Abstand zwischen Stichproben in verschiedenen Klassen maximiert und den Abstand innerhalb jeder Klasse minimiert.

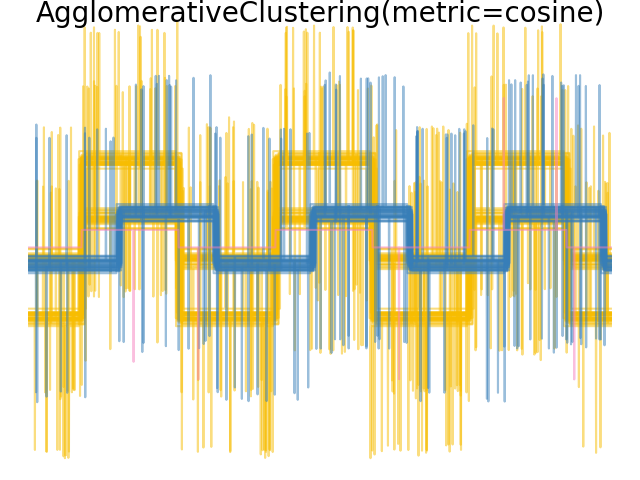
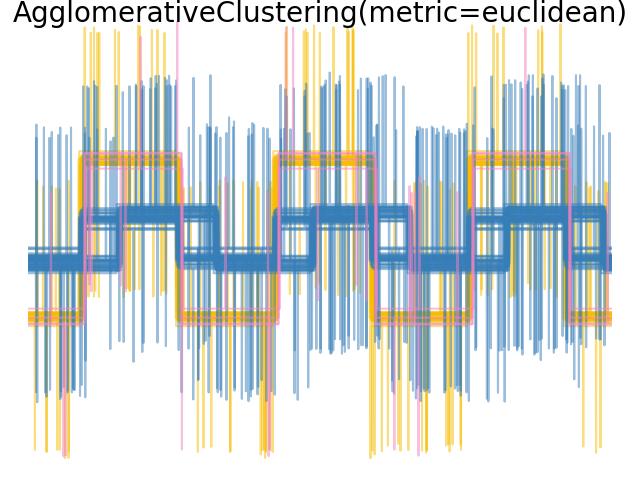
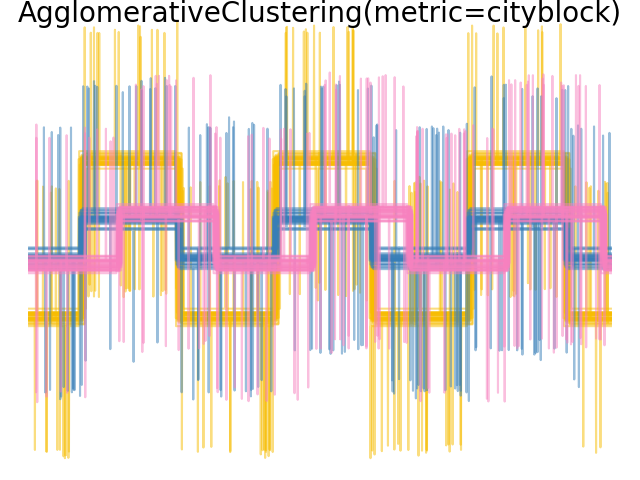
Beispiele

• Agglomeratives Clustering mit verschiedenen Metriken

2.3.6.5. Bisecting K-Means

Die BisectingKMeans ist eine iterative Variante von KMeans, die ein divisives hierarchisches Clustering verwendet. Anstatt alle Zentren auf einmal zu erstellen, werden die Zentren schrittweise basierend auf einem vorherigen Clustering ausgewählt: Ein Cluster wird wiederholt in zwei neue Cluster aufgeteilt, bis die gewünschte Anzahl von Clustern erreicht ist.

BisectingKMeans ist effizienter als KMeans, wenn die Anzahl der Cluster groß ist, da es bei jeder Bisektion nur auf einer Teilmenge der Daten arbeitet, während KMeans immer auf dem gesamten Datensatz arbeitet.

Obwohl BisectingKMeans von Natur aus nicht von den Vorteilen der "k-means++"-Initialisierung profitiert, liefert es dennoch vergleichbare Ergebnisse wie KMeans(init="k-means++") in Bezug auf die Trägheit zu geringeren Rechenkosten und wahrscheinlich bessere Ergebnisse als KMeans mit zufälliger Initialisierung.

Diese Variante ist effizienter als agglomeratives Clustering, wenn die Anzahl der Cluster im Vergleich zur Anzahl der Datenpunkte klein ist.

Diese Variante erzeugt auch keine leeren Cluster.

Es gibt zwei Strategien zur Auswahl des zu teilenden Clusters

• bisecting_strategy="largest_cluster" wählt den Cluster mit den meisten Punkten aus

• bisecting_strategy="biggest_inertia" wählt den Cluster mit der größten Trägheit (Cluster mit der größten Summe der quadrierten Fehler innerhalb) aus

Die Auswahl nach der größten Anzahl von Datenpunkten liefert in den meisten Fällen Ergebnisse, die genauso genau sind wie die Auswahl nach Trägheit, und ist schneller (insbesondere bei größeren Datenmengen, bei denen die Berechnung des Fehlers kostspielig sein kann).

Die Auswahl nach der größten Anzahl von Datenpunkten führt wahrscheinlich auch zu Clustern ähnlicher Größe, während KMeans dafür bekannt ist, Cluster unterschiedlicher Größe zu erzeugen.

Der Unterschied zwischen Bisecting K-Means und regulärem K-Means ist im Beispiel Vergleich der Leistung von Bisecting K-Means und regulärem K-Means zu sehen. Während der reguläre K-Means-Algorithmus dazu neigt, nicht zusammenhängende Cluster zu erzeugen, sind die Cluster von Bisecting K-Means gut geordnet und erzeugen eine ziemlich sichtbare Hierarchie.

Referenzen

• „A Comparison of Document Clustering Techniques“ Michael Steinbach, George Karypis und Vipin Kumar, Department of Computer Science and Engineering, University of Minnesota (Juni 2000)

• „Performance Analysis of K-Means and Bisecting K-Means Algorithms in Weblog Data“ K.Abirami und Dr.P.Mayilvahanan, International Journal of Emerging Technologies in Engineering Research (IJETER) Band 4, Ausgabe 8, (August 2016)

• „Bisecting K-means Algorithm Based on K-valued Self-determining and Clustering Center Optimization“ Jian Di, Xinyue Gou School of Control and Computer Engineering, North China Electric Power University, Baoding, Hebei, China (August 2017)

2.3.7. DBSCAN

Der DBSCAN-Algorithmus betrachtet Cluster als Bereiche hoher Dichte, die durch Bereiche geringer Dichte getrennt sind. Aufgrund dieser eher generischen Betrachtungsweise können von DBSCAN gefundene Cluster jede Form annehmen, im Gegensatz zu k-means, das davon ausgeht, dass Cluster konvex geformt sind. Die zentrale Komponente von DBSCAN ist das Konzept der Kernstichproben, bei denen es sich um Stichproben in Bereichen hoher Dichte handelt. Ein Cluster ist daher eine Menge von Kernstichproben, die jeweils nahe beieinander liegen (gemessen an einer bestimmten Distanzmetrik), und eine Menge von Nicht-Kernstichproben, die nahe an einer Kernstichprobe liegen (aber selbst keine Kernstichproben sind). Es gibt zwei Parameter für den Algorithmus, min_samples und eps, die formal definieren, was wir unter dicht verstehen. Höhere Werte für min_samples oder niedrigere Werte für eps bedeuten eine höhere Dichte, die zur Bildung eines Clusters erforderlich ist.

Genauer gesagt definieren wir eine Kernstichprobe als eine Stichprobe im Datensatz, für die es min_samples weitere Stichproben innerhalb einer Distanz von eps gibt, die als Nachbarn der Kernstichprobe definiert sind. Dies zeigt uns, dass die Kernstichprobe in einem dichten Bereich des Vektorraums liegt. Ein Cluster ist eine Menge von Kernstichproben, die rekursiv aufgebaut werden kann, indem man eine Kernstichprobe nimmt, alle ihre Nachbarn findet, die Kernstichproben sind, dann deren Nachbarn, die Kernstichproben sind, und so weiter. Ein Cluster hat auch eine Menge von Nicht-Kernstichproben, die Stichproben sind, die Nachbarn einer Kernstichprobe im Cluster sind, aber selbst keine Kernstichproben sind. Intuitiv befinden sich diese Stichproben am Rande eines Clusters.

Jede Kernstichprobe ist per Definition Teil eines Clusters. Jede Stichprobe, die keine Kernstichprobe ist und mindestens eps Distanz zu einer Kernstichprobe hat, wird vom Algorithmus als Ausreißer betrachtet.

Während der Parameter min_samples hauptsächlich steuert, wie tolerant der Algorithmus gegenüber Rauschen ist (bei verrauschten und großen Datensätzen kann es ratsam sein, diesen Parameter zu erhöhen), ist der Parameter eps entscheidend für die richtige Wahl für den Datensatz und die Distanzfunktion und kann normalerweise nicht mit dem Standardwert belassen werden. Er steuert die lokale Nachbarschaft der Punkte. Wenn er zu klein gewählt wird, wird der Großteil der Daten überhaupt nicht geclustert (und als -1 für "Rauschen" gekennzeichnet). Wenn er zu groß gewählt wird, werden nahe beieinander liegende Cluster zu einem einzigen Cluster zusammengeführt, und schließlich wird der gesamte Datensatz als ein einziger Cluster zurückgegeben. Einige Heuristiken zur Wahl dieses Parameters wurden in der Literatur diskutiert, z. B. basierend auf einem Knick in der Grafik der nächsten Nachbardistanzen (wie in den untenstehenden Referenzen diskutiert).

In der folgenden Abbildung zeigt die Farbe die Clusterzugehörigkeit an, wobei große Kreise die vom Algorithmus gefundenen Kernstichproben darstellen. Kleinere Kreise sind Nicht-Kernstichproben, die dennoch Teil eines Clusters sind. Außerdem sind die Ausreißer durch schwarze Punkte unten gekennzeichnet.

Beispiele

• Demo des DBSCAN Clustering Algorithmus

Implementierung

Der DBSCAN-Algorithmus ist deterministisch und erzeugt immer die gleichen Cluster, wenn ihm die gleichen Daten in der gleichen Reihenfolge präsentiert werden. Die Ergebnisse können jedoch abweichen, wenn die Daten in einer anderen Reihenfolge bereitgestellt werden. Erstens, obwohl die Kernstichproben immer denselben Clustern zugeordnet werden, hängt die Kennzeichnung dieser Cluster von der Reihenfolge ab, in der diese Stichproben in den Daten angetroffen werden. Zweitens und wichtiger ist, dass die Cluster, denen Nicht-Kernstichproben zugeordnet werden, je nach Datenreihenfolge unterschiedlich sein können. Dies würde geschehen, wenn eine Nicht-Kernstichprobe eine Distanz kleiner als eps zu zwei Kernstichproben in verschiedenen Clustern hat. Aufgrund der Dreiecksungleichung müssen diese beiden Kernstichproben mehr als eps voneinander entfernt sein, sonst wären sie im selben Cluster. Die Nicht-Kernstichprobe wird dem Cluster zugeordnet, der bei einem Durchlauf durch die Daten zuerst generiert wird, und so hängen die Ergebnisse von der Datenreihenfolge ab.

Die aktuelle Implementierung verwendet Ball Trees und KD-Trees, um die Nachbarschaft von Punkten zu bestimmen, was die Berechnung der vollständigen Distanzmatrix vermeidet (wie in scikit-learn-Versionen vor 0.14). Die Möglichkeit, benutzerdefinierte Metriken zu verwenden, bleibt erhalten; Details dazu finden Sie in NearestNeighbors.

Speicherverbrauch bei großen Stichprobengrößen

Diese Implementierung ist standardmäßig nicht speichereffizient, da sie eine vollständige paarweise Ähnlichkeitsmatrix erstellt, wenn keine KD-Bäume oder Ball-Bäume verwendet werden können (z. B. bei spärlichen Matrizen). Diese Matrix verbraucht \(n^2\) Gleitkommazahlen. Einige Mechanismen, um dies zu umgehen, sind:

• Verwenden Sie OPTICS-Clustering in Verbindung mit der Methode extract_dbscan. OPTICS-Clustering berechnet ebenfalls die vollständige paarweise Matrix, behält aber jeweils nur eine Zeile im Speicher (Speicherkomplexität \(\mathcal{O}(n)\)).

• Ein spärlicher Radius-Nachbarschaftsgraph (bei dem fehlende Einträge als außerhalb von eps angenommen werden) kann speichereffizient vorab berechnet werden, und DBSCAN kann über diesen mit metric='precomputed' ausgeführt werden. Siehe sklearn.neighbors.NearestNeighbors.radius_neighbors_graph.

• Der Datensatz kann komprimiert werden, entweder durch Entfernen exakter Duplikate, falls diese in Ihren Daten vorkommen, oder durch Verwendung von BIRCH. Dann haben Sie nur noch eine relativ kleine Anzahl von Vertretern für eine große Anzahl von Punkten. Sie können dann ein sample_weight beim Anpassen von DBSCAN angeben.

Referenzen

• A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise Ester, M., H. P. Kriegel, J. Sander und X. Xu, In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, AAAI Press, S. 226-231. 1996.

• DBSCAN revisited, revisited: why and how you should (still) use DBSCAN. Schubert, E., Sander, J., Ester, M., Kriegel, H. P. & Xu, X. (2017). In ACM Transactions on Database Systems (TODS), 42(3), 19.

2.3.8. HDBSCAN

Der Algorithmus HDBSCAN kann als Erweiterung von DBSCAN und OPTICS betrachtet werden. Insbesondere geht DBSCAN davon aus, dass das Clustering-Kriterium (d. h. die Dichteanforderung) global homogen ist. Mit anderen Worten, DBSCAN kann Schwierigkeiten haben, Cluster mit unterschiedlichen Dichten erfolgreich zu erfassen. HDBSCAN mildert diese Annahme und untersucht alle möglichen Dichteskalen, indem es eine alternative Darstellung des Clustering-Problems erstellt.

Hinweis

Diese Implementierung ist an die ursprüngliche Implementierung von HDBSCAN, scikit-learn-contrib/hdbscan, basierend auf [LJ2017], angepasst.

Beispiele

• Demo des HDBSCAN Clustering Algorithmus

2.3.8.1. Mutual Reachability Graph

HDBSCAN definiert zuerst \(d_c(x_p)\), die Kerndistanz einer Stichprobe \(x_p\), als die Distanz zu ihrem min_samples-ten nächsten Nachbarn, sich selbst mitzählend. Zum Beispiel, wenn min_samples=5 und \(x_*\) der 5. nächste Nachbar von \(x_p\) ist, dann ist die Kerndistanz

\[d_c(x_p)=d(x_p, x_*).\]

Als Nächstes definiert es \(d_m(x_p, x_q)\), die gegenseitige Erreichbarkeitsdistanz zweier Punkte \(x_p, x_q\), als

\[d_m(x_p, x_q) = \max\{d_c(x_p), d_c(x_q), d(x_p, x_q)\}\]

Diese beiden Konzepte ermöglichen es uns, den gegenseitigen Erreichbarkeitsgraphen \(G_{ms}\) zu konstruieren, der für eine feste Wahl von min_samples definiert ist, indem jede Stichprobe \(x_p\) mit einem Knoten des Graphen assoziiert wird, und somit Kanten zwischen Punkten \(x_p, x_q\) die gegenseitige Erreichbarkeitsdistanz \(d_m(x_p, x_q)\) zwischen ihnen sind. Wir können Teilmengen dieses Graphen, bezeichnet als \(G_{ms,\varepsilon}\), aufbauen, indem wir alle Kanten mit einem Wert größer als \(\varepsilon\) entfernen: aus dem ursprünglichen Graphen. Alle Punkte, deren Kerndistanz kleiner als \(\varepsilon\) ist, werden in diesem Stadium als Rauschen markiert. Die verbleibenden Punkte werden dann durch Finden der zusammenhängenden Komponenten dieses getrimmten Graphen geclustert.

Hinweis

Das Nehmen der zusammenhängenden Komponenten eines getrimmten Graphen \(G_{ms,\varepsilon}\) ist äquivalent zum Ausführen von DBSCAN* mit min_samples und \(\varepsilon\). DBSCAN* ist eine leicht modifizierte Version von DBSCAN, die in [CM2013] erwähnt wird.

2.3.8.2. Hierarchisches Clustering

HDBSCAN kann als ein Algorithmus betrachtet werden, der DBSCAN*-Clustering über alle Werte von \(\varepsilon\) durchführt. Wie bereits erwähnt, ist dies äquivalent zum Finden der zusammenhängenden Komponenten der gegenseitigen Erreichbarkeitsgraphen für alle Werte von \(\varepsilon\). Um dies effizient zu tun, extrahiert HDBSCAN zuerst einen minimalen Spannbaum (MST) aus dem vollständig verbundenen gegenseitigen Erreichbarkeitsgraphen und schneidet dann gierig die Kanten mit dem höchsten Gewicht ab. Eine Übersicht über den HDBSCAN-Algorithmus ist wie folgt:

1. Extrahieren Sie den MST von \(G_{ms}\).

2. Erweitern Sie den MST durch Hinzufügen einer "Selbstkante" für jeden Knoten mit einem Gewicht, das der Kerndistanz der zugrunde liegenden Stichprobe entspricht.

3. Initialisieren Sie einen einzelnen Cluster und ein Label für den MST.

4. Entfernen Sie die Kante mit dem größten Gewicht aus dem MST (Gleichstände werden gleichzeitig entfernt).

5. Weisen Sie den zusammenhängenden Komponenten, die die Endpunkte der nun entfernten Kante enthalten, Cluster-Labels zu. Wenn die Komponente keine Kante hat, wird ihr stattdessen ein "Null"-Label zugewiesen, das sie als Rauschen kennzeichnet.

6. Wiederholen Sie 4-5, bis keine verbundenen Komponenten mehr vorhanden sind.

HDBSCAN ist daher in der Lage, alle möglichen Partitionen zu erhalten, die von DBSCAN* für eine feste Wahl von min_samples in hierarchischer Weise erreichbar sind. Tatsächlich ermöglicht dies HDBSCAN, Clustering über mehrere Dichten hinweg durchzuführen, und daher benötigt es \(\varepsilon\) nicht mehr als Hyperparameter. Stattdessen stützt es sich ausschließlich auf die Wahl von min_samples, was tendenziell ein robusterer Hyperparameter ist.

HDBSCAN kann mit einem zusätzlichen Hyperparameter min_cluster_size geglättet werden, der angibt, dass während des hierarchischen Clusterings Komponenten mit weniger als minimum_cluster_size Stichproben als Rauschen betrachtet werden. In der Praxis kann man minimum_cluster_size = min_samples setzen, um die Parameter zu koppeln und den Hyperparameterraum zu vereinfachen.

Referenzen

[CM2013]

Campello, R.J.G.B., Moulavi, D., Sander, J. (2013). Density-Based Clustering Based on Hierarchical Density Estimates. In: Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G. (Hrsg.) Advances in Knowledge Discovery and Data Mining. PAKDD 2013. Lecture Notes in Computer Science(), Bd. 7819. Springer, Berlin, Heidelberg. Density-Based Clustering Based on Hierarchical Density Estimates

[LJ2017]

L. McInnes und J. Healy, (2017). Accelerated Hierarchical Density Based Clustering. In: IEEE International Conference on Data Mining Workshops (ICDMW), 2017, S. 33-42. Accelerated Hierarchical Density Based Clustering

2.3.9. OPTICS

Der OPTICS-Algorithmus weist viele Ähnlichkeiten mit dem DBSCAN-Algorithmus auf und kann als eine Verallgemeinerung von DBSCAN betrachtet werden, die die eps-Anforderung von einem einzelnen Wert auf einen Wertebereich erweitert. Der Hauptunterschied zwischen DBSCAN und OPTICS besteht darin, dass der OPTICS-Algorithmus einen Erreichbarkeitsgraphen aufbaut, der jedem Sample sowohl eine reachability_-Distanz als auch eine Position im Cluster-Attribut ordering_ zuweist; diese beiden Attribute werden zugewiesen, wenn das Modell trainiert wird, und zur Bestimmung der Cluster-Mitgliedschaft verwendet. Wenn OPTICS mit dem Standardwert inf für max_eps ausgeführt wird, kann die DBSCAN-artige Cluster-Extraktion für jeden gegebenen eps-Wert mit der Methode cluster_optics_dbscan in linearer Zeit wiederholt durchgeführt werden. Das Setzen von max_eps auf einen niedrigeren Wert führt zu kürzeren Laufzeiten und kann als der maximale Nachbarschaftsradius jedes Punktes betrachtet werden, um andere potenziell erreichbare Punkte zu finden.

Die von OPTICS generierten Erreichbarkeitsdistanzen ermöglichen eine variable Dichte-Extraktion von Clustern innerhalb eines einzelnen Datensatzes. Wie im obigen Diagramm gezeigt, erzeugt die Kombination von Erreichbarkeitsdistanzen und dem ordering_ des Datensatzes ein Erreichbarkeitsdiagramm, bei dem die Punktdichte auf der Y-Achse dargestellt wird und die Punkte so geordnet sind, dass benachbarte Punkte nebeneinander liegen. Das „Schneiden“ des Erreichbarkeitsdiagramms bei einem einzelnen Wert ergibt DBSCAN-ähnliche Ergebnisse; alle Punkte über dem „Schnitt“ werden als Rauschen klassifiziert, und jedes Mal, wenn beim Lesen von links nach rechts eine Unterbrechung auftritt, bedeutet dies einen neuen Cluster. Die Standard-Cluster-Extraktion mit OPTICS betrachtet die steilen Hänge im Diagramm, um Cluster zu finden, und der Benutzer kann mit dem Parameter xi definieren, was als steiler Hang gilt. Es gibt auch andere Möglichkeiten zur Analyse des Diagramms selbst, wie z. B. die Erzeugung hierarchischer Darstellungen der Daten durch Erreichbarkeitsdiagramm-Dendrogramme, und die Hierarchie der vom Algorithmus erkannten Cluster kann über den Parameter cluster_hierarchy_ abgerufen werden. Das obige Diagramm wurde farblich kodiert, sodass die Clusterfarben im ebenen Raum den linearen Segmentclustern des Erreichbarkeitsdiagramms entsprechen. Beachten Sie, dass die blauen und roten Cluster im Erreichbarkeitsdiagramm nebeneinander liegen und hierarchisch als Kinder eines größeren übergeordneten Clusters dargestellt werden können.

Beispiele

• Demo des OPTICS Clustering Algorithmus

Vergleich mit DBSCAN

Die Ergebnisse der Methode cluster_optics_dbscan von OPTICS und DBSCAN sind sehr ähnlich, aber nicht immer identisch; insbesondere die Kennzeichnung von peripheren und Rauschpunkten. Dies liegt zum Teil daran, dass die ersten Samples jedes dichten Bereichs, die von OPTICS verarbeitet werden, einen hohen Erreichbarkeitswert haben, während sie sich in ihrer Nähe zu anderen Punkten in ihrem Bereich befinden, und daher manchmal als Rauschen statt als peripher gekennzeichnet werden. Dies wirkt sich auf benachbarte Punkte aus, wenn diese als Kandidaten für die Kennzeichnung als peripher oder Rauschen betrachtet werden.

Beachten Sie, dass DBSCAN für jeden einzelnen eps-Wert tendenziell eine kürzere Laufzeit als OPTICS hat; für wiederholte Läufe mit unterschiedlichen eps-Werten kann jedoch ein einzelner Lauf von OPTICS eine geringere kumulative Laufzeit erfordern als DBSCAN. Es ist auch wichtig zu beachten, dass die Ausgabe von OPTICS nur dann nahe an der von DBSCAN liegt, wenn eps und max_eps nahe beieinander liegen.

Rechenkomplexität

Räumliche Indexierungsbäume werden verwendet, um die Berechnung der vollständigen Distanzmatrix zu vermeiden und eine effiziente Speichernutzung auf großen Stichprobenmengen zu ermöglichen. Unterschiedliche Distanzmetriken können über das Schlüsselwort metric bereitgestellt werden.

Für große Datensätze können ähnliche (aber nicht identische) Ergebnisse über HDBSCAN erzielt werden. Die HDBSCAN-Implementierung ist Multithreaded und hat eine bessere algorithmische Laufzeitkomplexität als OPTICS, auf Kosten einer schlechteren Speicherperformance. Für extrem große Datensätze, die den Systemarbeitsspeicher mit HDBSCAN erschöpfen, behält OPTICS eine Speicherkomplexität von \(n\) (im Gegensatz zu \(n^2\)); die Abstimmung des Parameters max_eps wird jedoch wahrscheinlich benötigt, um eine Lösung in einer angemessenen Wandzeit zu erhalten.

Referenzen

• „OPTICS: ordering points to identify the clustering structure.“ Ankerst, Mihael, Markus M. Breunig, Hans-Peter Kriegel und Jörg Sander. In ACM Sigmod Record, Bd. 28, Nr. 2, S. 49-60. ACM, 1999.

2.3.10. BIRCH

Der Birch erstellt einen Baum namens Clustering Feature Tree (CFT) für die gegebenen Daten. Die Daten werden im Wesentlichen verlustbehaftet in eine Reihe von Clustering Feature Nodes (CF Nodes) komprimiert. Die CF Nodes haben eine Anzahl von Unterclustern, die Clustering Feature Subclusters (CF Subclusters) genannt werden, und diese CF Subclusters in den nicht-terminalen CF Nodes können CF Nodes als Kinder haben.

Die CF Subclusters speichern die notwendigen Informationen für die Clusterbildung, wodurch die Notwendigkeit, die gesamten Eingabedaten im Speicher zu halten, entfällt. Diese Informationen umfassen

• Anzahl der Samples in einem Subcluster.

• Lineare Summe – Ein n-dimensionaler Vektor, der die Summe aller Samples enthält.

• Quadratische Summe – Summe der quadrierten L2-Norm aller Samples.

• Zentroiden – Um Neuberechnungen zu vermeiden: lineare Summe / n_samples.

• Quadrierte Norm der Zentroiden.

Der BIRCH-Algorithmus hat zwei Parameter: den Schwellenwert und den Verzweigungsfaktor. Der Verzweigungsfaktor begrenzt die Anzahl der Subcluster in einem Knoten, und der Schwellenwert begrenzt den Abstand zwischen dem eintretenden Sample und den vorhandenen Subclustern.

Dieser Algorithmus kann als eine Instanz einer Datenreduktionsmethode betrachtet werden, da er die Eingabedaten auf eine Menge von Subclustern reduziert, die direkt aus den Blättern des CFT gewonnen werden. Diese reduzierten Daten können weiter verarbeitet werden, indem sie in einen globalen Clusterer eingespeist werden. Dieser globale Clusterer kann durch n_clusters eingestellt werden. Wenn n_clusters auf None gesetzt ist, werden die Subcluster direkt aus den Blättern ausgelesen, andernfalls wird ein globaler Clustering-Schritt diese Subcluster in globale Cluster (Labels) einteilt, und die Samples werden dem globalen Label des nächstgelegenen Subclusters zugeordnet.

Algorithmusbeschreibung

• Ein neues Sample wird in die Wurzel des CF-Baums eingefügt, die ein CF-Knoten ist. Es wird dann mit dem Subcluster der Wurzel zusammengeführt, der nach der Zusammenführung den kleinsten Radius aufweist, beschränkt durch die Schwellenwert- und Verzweigungsfaktorbedingungen. Wenn der Subcluster ein Kind-Knoten hat, wird dies wiederholt, bis ein Blatt erreicht wird. Nach dem Finden des nächstgelegenen Subclusters im Blatt werden die Eigenschaften dieses Subclusters und der übergeordneten Subcluster rekursiv aktualisiert.

• Wenn der Radius des Subclusters, der durch das Zusammenführen des neuen Samples und des nächstgelegenen Subclusters erhalten wird, größer als das Quadrat des Schwellenwerts ist und die Anzahl der Subcluster größer als der Verzweigungsfaktor ist, wird vorübergehend Speicher für dieses neue Sample zugewiesen. Die beiden am weitesten entfernten Subcluster werden genommen, und die Subcluster werden auf der Grundlage des Abstands zwischen diesen Subclustern in zwei Gruppen aufgeteilt.

• Wenn dieser aufgeteilte Knoten einen übergeordneten Subcluster hat und Platz für einen neuen Subcluster vorhanden ist, wird der übergeordnete Knoten in zwei aufgeteilt. Wenn kein Platz vorhanden ist, wird dieser Knoten erneut in zwei aufgeteilt, und der Vorgang wird rekursiv fortgesetzt, bis die Wurzel erreicht ist.

BIRCH oder MiniBatchKMeans?

• BIRCH skaliert nicht sehr gut auf hochdimensionale Daten. Als Faustregel gilt: Wenn n_features größer als zwanzig ist, ist es im Allgemeinen besser, MiniBatchKMeans zu verwenden.

• Wenn die Anzahl der Dateninstanzen reduziert werden muss oder wenn man eine große Anzahl von Subclustern als Vorverarbeitungsschritt oder anderweitig wünscht, ist BIRCH nützlicher als MiniBatchKMeans.

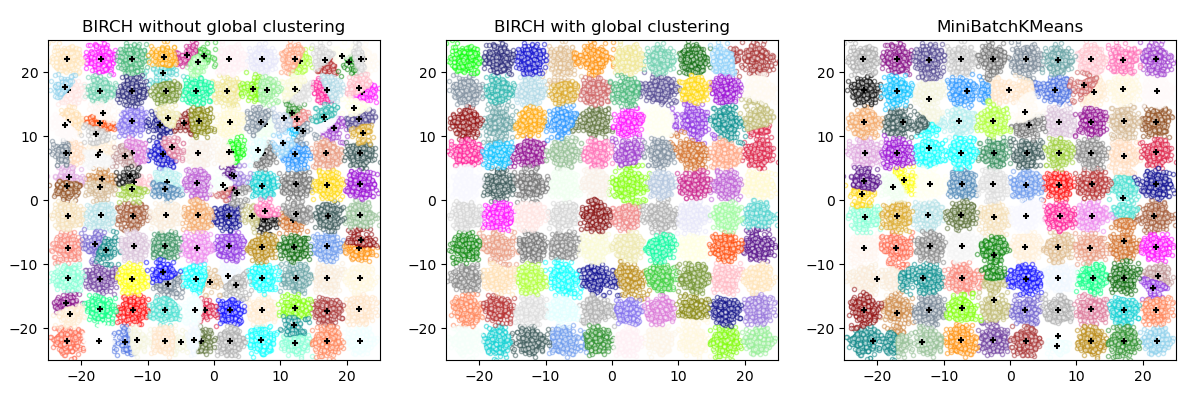
Wie benutzt man partial_fit?

Um die Berechnung des globalen Clusterings zu vermeiden, wird dem Benutzer für jeden Aufruf von partial_fit empfohlen,

1. zuerst n_clusters=None zu setzen.

2. Alle Daten durch mehrfache Aufrufe von partial_fit zu trainieren.

3. n_clusters mit brc.set_params(n_clusters=n_clusters) auf den gewünschten Wert zu setzen.

4. Abschließend partial_fit ohne Argumente aufzurufen, d. h. brc.partial_fit(), was das globale Clustering durchführt.

Referenzen

• Tian Zhang, Raghu Ramakrishnan, Maron Livny BIRCH: An efficient data clustering method for large databases. https://www.cs.sfu.ca/CourseCentral/459/han/papers/zhang96.pdf

• Roberto Perdisci JBirch - Java-Implementierung des BIRCH-Clustering-Algorithmus https://code.google.com/archive/p/jbirch

2.3.11. Evaluierung der Clustering-Leistung

Die Leistung eines Clustering-Algorithmus zu bewerten ist nicht so trivial wie das Zählen der Fehler oder die Präzision und der Rückruf eines überwachten Klassifizierungsalgorithmus. Insbesondere sollte jede Bewertungsmetrik nicht die absoluten Werte der Cluster-Labels berücksichtigen, sondern vielmehr, ob diese Clusterbildung Trennungen der Daten ähnlich einer Ground-Truth-Klassensammlung definiert oder eine Annahme erfüllt, dass Mitglieder derselben Klasse ähnlicher sind als Mitglieder unterschiedlicher Klassen gemäß einer Ähnlichkeitsmetrik.

2.3.11.1. Rand-Index

Gegeben die Kenntnis der Ground-Truth-Klassenzuweisungen labels_true und unserer Clustering-Algorithmus-Zuweisungen derselben Samples labels_pred, ist der (angepasste oder nicht angepasste) Rand-Index eine Funktion, die die Ähnlichkeit der beiden Zuweisungen misst und Permutationen ignoriert.

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.rand_score(labels_true, labels_pred)
0.66

Der Rand-Index stellt nicht sicher, dass für eine zufällige Beschriftung ein Wert nahe 0,0 erzielt wird. Der angepasste Rand-Index korrigiert für Zufälligkeit und liefert eine solche Basislinie.

>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24

Wie bei allen Clustering-Metriken kann man 0 und 1 in den vorhergesagten Labels vertauschen, 2 in 3 umbenennen und denselben Score erhalten.

>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.rand_score(labels_true, labels_pred)
0.66
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24

Darüber hinaus sind sowohl rand_score als auch adjusted_rand_score symmetrisch: Das Vertauschen der Argumente ändert die Scores nicht. Sie können daher als Konsensmaßstäbe verwendet werden.

>>> metrics.rand_score(labels_pred, labels_true)
0.66
>>> metrics.adjusted_rand_score(labels_pred, labels_true)
0.24

Perfekte Beschriftung wird mit 1,0 bewertet.

>>> labels_pred = labels_true[:]
>>> metrics.rand_score(labels_true, labels_pred)
1.0
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
1.0

Schlecht übereinstimmende Labels (z. B. unabhängige Labelings) haben niedrigere Scores, und für den angepassten Rand-Index ist der Score negativ oder nahe Null. Für den nicht angepassten Rand-Index ist der Score jedoch zwar niedriger, aber nicht unbedingt nahe Null.

>>> labels_true = [0, 0, 0, 0, 0, 0, 1, 1]
>>> labels_pred = [0, 1, 2, 3, 4, 5, 5, 6]
>>> metrics.rand_score(labels_true, labels_pred)
0.39
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
-0.072

Vorteile

• Interpretierbarkeit: Der nicht angepasste Rand-Index ist proportional zur Anzahl der Sample-Paare, deren Labels sowohl in labels_pred als auch in labels_true gleich sind oder in beiden unterschiedlich sind.

• Zufällige (gleichmäßige) Label-Zuweisungen haben einen angepassten Rand-Index-Score nahe 0,0 für jeden Wert von n_clusters und n_samples (was nicht der Fall ist für den nicht angepassten Rand-Index oder die V-Messung zum Beispiel).

• Begrenzter Bereich: Niedrigere Werte deuten auf unterschiedliche Label-Zuweisungen hin, ähnliche Clusterbildungen haben einen hohen (angepassten oder nicht angepassten) Rand-Index, 1,0 ist der perfekte Übereinstimmungsscore. Der Score-Bereich ist [0, 1] für den nicht angepassten Rand-Index und [-0,5, 1] für den angepassten Rand-Index.

• Keine Annahme über die Clusterstruktur: Der (angepasste oder nicht angepasste) Rand-Index kann verwendet werden, um alle Arten von Clustering-Algorithmen zu vergleichen und kann verwendet werden, um Clustering-Algorithmen wie k-means, die isostropische Blob-Formen annehmen, mit Ergebnissen von spektralen Clustering-Algorithmen, die Cluster mit „gefalteten“ Formen finden können, zu vergleichen.

Nachteile

• Im Gegensatz zur Trägheit erfordert der (angepasste oder nicht angepasste) Rand-Index die Kenntnis der Ground-Truth-Klassen, die in der Praxis fast nie verfügbar sind oder eine manuelle Zuweisung durch menschliche Annotatoren erfordern (wie im überwachten Lernsetting).

  Der (angepasste oder nicht angepasste) Rand-Index kann jedoch auch in einem rein unüberwachten Setting als Baustein für einen Konsens-Index nützlich sein, der für die Auswahl von Clustering-Modellen verwendet werden kann (TODO).

• Der nicht angepasste Rand-Index liegt oft nahe bei 1,0, auch wenn die Clusterbildungen selbst stark voneinander abweichen. Dies kann verstanden werden, wenn man den Rand-Index als Genauigkeit der Elementpaarkennzeichnung interpretiert, die sich aus den Clusterbildungen ergibt: In der Praxis gibt es oft eine Mehrheit von Elementpaaren, denen sowohl unter der vorhergesagten als auch unter der Ground-Truth-Clusterbildung das Label unterschiedlich zugewiesen wird, was zu einem hohen Anteil von übereinstimmenden Paare-Labels führt, was anschließend zu einem hohen Score führt.

Beispiele

• Anpassung für Zufälligkeit bei der Bewertung der Clustering-Leistung: Analyse des Einflusses der Datensatzgröße auf den Wert von Clustering-Metriken für zufällige Zuweisungen.

Mathematische Formulierung

Wenn C eine Ground-Truth-Klassen-Zuweisung und K die Clusterbildung ist, definieren wir \(a\) und \(b\) als

• \(a\), die Anzahl der Paare von Elementen, die in C in derselben Menge und in K in derselben Menge sind.

• \(b\), die Anzahl der Paare von Elementen, die in C in unterschiedlichen Mengen und in K in unterschiedlichen Mengen sind.

Der nicht angepasste Rand-Index ist dann gegeben durch

\[\text{RI} = \frac{a + b}{C_2^{n_{samples}}}\]

wobei \(C_2^{n_{samples}}\) die Gesamtzahl möglicher Paare im Datensatz ist. Es spielt keine Rolle, ob die Berechnung auf geordneten oder ungeordneten Paaren durchgeführt wird, solange die Berechnung konsistent durchgeführt wird.

Der Rand-Index garantiert jedoch nicht, dass zufällige Label-Zuweisungen einen Wert nahe Null erhalten (insbesondere wenn die Anzahl der Cluster von ähnlicher Größenordnung wie die Anzahl der Samples ist).

Um diesen Effekt zu kompensieren, können wir den erwarteten RI \(E[\text{RI}]\) von zufälligen Labelings abziehen, indem wir den angepassten Rand-Index wie folgt definieren:

\[\text{ARI} = \frac{\text{RI} - E[\text{RI}]}{\max(\text{RI}) - E[\text{RI}]}\]

Referenzen

• Comparing Partitions L. Hubert und P. Arabie, Journal of Classification 1985

• Properties of the Hubert-Arabie adjusted Rand index D. Steinley, Psychological Methods 2004

• Wikipedia-Eintrag für den Rand-Index

• Minimum adjusted Rand index for two clusterings of a given size, 2022, J. E. Chacón und A. I. Rastrojo

2.3.11.2. Mutual Information-basierte Scores

Gegeben die Kenntnis der Ground-Truth-Klassenzuweisungen der Samples, ist der Mutual Information eine Funktion, die die Übereinstimmung der beiden Zuweisungen misst und Permutationen ignoriert. Zwei verschiedene normalisierte Versionen dieses Maßes sind verfügbar: Normalized Mutual Information (NMI) und Adjusted Mutual Information (AMI). NMI wird oft in der Literatur verwendet, während AMI neuer vorgeschlagen wurde und gegen Zufälligkeit normalisiert ist.

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504

Man kann 0 und 1 in den vorhergesagten Labels vertauschen, 2 in 3 umbenennen und denselben Score erhalten.

>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504

Alle, mutual_info_score, adjusted_mutual_info_score und normalized_mutual_info_score sind symmetrisch: Das Vertauschen der Argumente ändert den Score nicht. Daher können sie als Konsensmaßstäbe verwendet werden.

>>> metrics.adjusted_mutual_info_score(labels_pred, labels_true)
0.22504

Perfekte Beschriftung wird mit 1,0 bewertet.

>>> labels_pred = labels_true[:]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
1.0

>>> metrics.normalized_mutual_info_score(labels_true, labels_pred)
1.0

Dies gilt nicht für mutual_info_score, die daher schwerer zu beurteilen ist.

>>> metrics.mutual_info_score(labels_true, labels_pred)
0.69

Schlecht (z. B. unabhängige Labelings) haben nicht-positive Scores.

>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
-0.10526

Vorteile

• Zufällige (gleichmäßige) Label-Zuweisungen haben einen AMI-Score nahe 0,0 für jeden Wert von n_clusters und n_samples (was nicht der Fall ist für rohe Mutual Information oder die V-Messung zum Beispiel).

• Obere Grenze von 1: Werte nahe Null deuten auf zwei Label-Zuweisungen hin, die weitgehend unabhängig sind, während Werte nahe Eins erhebliche Übereinstimmung bedeuten. Darüber hinaus bedeutet ein AMI von genau 1, dass die beiden Label-Zuweisungen gleich sind (mit oder ohne Permutation).

Nachteile

• Im Gegensatz zur Trägheit erfordern MI-basierte Maßnahmen die Kenntnis der Ground-Truth-Klassen, die in der Praxis fast nie verfügbar sind oder eine manuelle Zuweisung durch menschliche Annotatoren erfordern (wie im überwachten Lernsetting).

  MI-basierte Maßnahmen können jedoch auch in einem rein unüberwachten Setting als Baustein für einen Konsens-Index nützlich sein, der für die Auswahl von Clustering-Modellen verwendet werden kann.

• NMI und MI sind nicht gegen Zufälligkeit angepasst.

Beispiele

• Anpassung für Zufälligkeit bei der Bewertung der Clustering-Leistung: Analyse des Einflusses der Datensatzgröße auf den Wert von Clustering-Metriken für zufällige Zuweisungen. Dieses Beispiel enthält auch den Adjusted Rand Index.

Mathematische Formulierung

Angenommen, zwei Label-Zuweisungen (derselben N Objekte), \(U\) und \(V\). Ihre Entropie ist das Ausmaß der Unsicherheit für eine Partitionmenge, definiert als

\[H(U) = - \sum_{i=1}^{|U|}P(i)\log(P(i))\]

wobei \(P(i) = |U_i| / N\) die Wahrscheinlichkeit ist, dass ein zufällig ausgewähltes Objekt aus \(U\) in die Klasse \(U_i\) fällt. Ebenso für \(V\)

\[H(V) = - \sum_{j=1}^{|V|}P'(j)\log(P'(j))\]

mit \(P'(j) = |V_j| / N\). Die gegenseitige Information (MI) zwischen \(U\) und \(V\) wird berechnet durch

\[\text{MI}(U, V) = \sum_{i=1}^{|U|}\sum_{j=1}^{|V|}P(i, j)\log\left(\frac{P(i,j)}{P(i)P'(j)}\right)\]

wobei \(P(i, j) = |U_i \cap V_j| / N\) die Wahrscheinlichkeit ist, dass ein zufällig ausgewähltes Objekt in beide Klassen \(U_i\) und \(V_j\) fällt.

Es kann auch in Mengen-Kardinalitätsformulation ausgedrückt werden:

\[\text{MI}(U, V) = \sum_{i=1}^{|U|} \sum_{j=1}^{|V|} \frac{|U_i \cap V_j|}{N}\log\left(\frac{N|U_i \cap V_j|}{|U_i||V_j|}\right)\]

Die normalisierte gegenseitige Information ist definiert als

\[\text{NMI}(U, V) = \frac{\text{MI}(U, V)}{\text{mean}(H(U), H(V))}\]

Dieser Wert der gegenseitigen Information und auch die normalisierte Variante sind nicht gegen Zufälligkeit angepasst und tendieren dazu, mit zunehmender Anzahl verschiedener Labels (Cluster) zu steigen, unabhängig vom tatsächlichen Ausmaß der „gegenseitigen Information“ zwischen den Label-Zuweisungen.

Der Erwartungswert für die gegenseitige Information kann mit der folgenden Gleichung [VEB2009] berechnet werden. In dieser Gleichung sind \(a_i = |U_i|\) (die Anzahl der Elemente in \(U_i\)) und \(b_j = |V_j|\) (die Anzahl der Elemente in \(V_j\)).

\[E[\text{MI}(U,V)]=\sum_{i=1}^{|U|} \sum_{j=1}^{|V|} \sum_{n_{ij}=(a_i+b_j-N)^+ }^{\min(a_i, b_j)} \frac{n_{ij}}{N}\log \left( \frac{ N.n_{ij}}{a_i b_j}\right) \frac{a_i!b_j!(N-a_i)!(N-b_j)!}{N!n_{ij}!(a_i-n_{ij})!(b_j-n_{ij})! (N-a_i-b_j+n_{ij})!}\]

Unter Verwendung des Erwartungswerts kann die angepasste gegenseitige Information dann in einer ähnlichen Form wie die des angepassten Rand-Index berechnet werden.

\[\text{AMI} = \frac{\text{MI} - E[\text{MI}]}{\text{mean}(H(U), H(V)) - E[\text{MI}]}\]

Für normalisierte gegenseitige Information und angepasste gegenseitige Information ist der normalisierende Wert typischerweise ein generalisierter Mittelwert der Entropien jeder Clusterbildung. Verschiedene verallgemeinerte Mittel existieren, und es gibt keine festen Regeln, um eine über die anderen zu bevorzugen. Die Entscheidung basiert weitgehend auf den jeweiligen Fachgebieten; zum Beispiel ist in der Community-Erkennung der arithmetische Mittelwert am gebräuchlichsten. Jede normalisierende Methode liefert „qualitativ ähnliche Verhaltensweisen“ [YAT2016]. In unserer Implementierung wird dies durch den Parameter average_method gesteuert.

Vinh et al. (2010) nannten Varianten von NMI und AMI nach ihrer Mittelungsmethode [VEB2010]. Ihre ‚sqrt‘- und ‚sum‘-Mittel sind das geometrische und arithmetische Mittel; wir verwenden diese gebräuchlicheren Namen.

Referenzen

• Strehl, Alexander und Joydeep Ghosh (2002). „Cluster ensembles – a knowledge reuse framework for combining multiple partitions“. Journal of Machine Learning Research 3: 583-617. doi:10.1162/153244303321897735.

• Wikipedia-Eintrag für die (normalisierte) Mutual Information

• Wikipedia-Eintrag für die Adjusted Mutual Information

[VEB2009]

Vinh, Epps und Bailey, (2009). „Information theoretic measures for clusterings comparison“. Proceedings of the 26th Annual International Conference on Machine Learning - ICML ‘09. doi:10.1145/1553374.1553511. ISBN 9781605585161.

[VEB2010]

Vinh, Epps und Bailey, (2010). „Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance“. JMLR <https://jmlr.csail.mit.edu/papers/volume11/vinh10a/vinh10a.pdf>

[YAT2016]

Yang, Algesheimer und Tessone, (2016). „A comparative analysis of community detection algorithms on artificial networks“. Scientific Reports 6: 30750. doi:10.1038/srep30750.

2.3.11.3. Homogenität, Vollständigkeit und V-Maß

Gegeben die Kenntnis der Ground-Truth-Klassenzuweisungen der Samples ist es möglich, einige intuitive Metriken unter Verwendung der bedingten Entropieanalyse zu definieren.

Insbesondere definieren Rosenberg und Hirschberg (2007) die folgenden beiden wünschenswerten Ziele für jede Cluster-Zuweisung:

• Homogenität: Jeder Cluster enthält nur Mitglieder einer einzigen Klasse.

• Vollständigkeit: Alle Elemente einer gegebenen Klasse werden demselben Cluster zugeordnet.

Wir können diese Konzepte in Punktzahlen umwandeln: homogeneity_score und completeness_score. Beide sind nach unten durch 0,0 und nach oben durch 1,0 begrenzt (höher ist besser).

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.homogeneity_score(labels_true, labels_pred)
0.66

>>> metrics.completeness_score(labels_true, labels_pred)
0.42

Ihr harmonisches Mittel, die V-Messung, wird durch v_measure_score berechnet.

>>> metrics.v_measure_score(labels_true, labels_pred)
0.516

Die Formel dieser Funktion lautet:

\[v = \frac{(1 + \beta) \times \text{homogenität} \times \text{vollständigkeit}}{(\beta \times \text{homogenität} + \text{vollständigkeit})}\]

beta hat standardmäßig den Wert 1,0. Bei der Verwendung eines Wertes kleiner als 1 für beta

>>> metrics.v_measure_score(labels_true, labels_pred, beta=0.6)
0.547

wird der Homogenität mehr Gewicht verliehen, und bei der Verwendung eines Wertes größer als 1

>>> metrics.v_measure_score(labels_true, labels_pred, beta=1.8)
0.48

wird der Vollständigkeit mehr Gewicht verliehen.

Die V-Messung ist tatsächlich äquivalent zur zuvor diskutierten Mutual Information (NMI), wobei die Aggregationsfunktion das arithmetische Mittel ist [B2011].

Homogenität, Vollständigkeit und V-Messung können gleichzeitig mit homogeneity_completeness_v_measure wie folgt berechnet werden.

>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(0.67, 0.42, 0.52)

Die folgende Cluster-Zuordnung ist geringfügig besser, da sie homogen, aber nicht vollständig ist.

>>> labels_pred = [0, 0, 0, 1, 2, 2]
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(1.0, 0.68, 0.81)

Hinweis

v_measure_score ist symmetrisch: Sie kann verwendet werden, um die Übereinstimmung zweier unabhängiger Zuordnungen auf demselben Datensatz zu bewerten.

Dies ist bei completeness_score und homogeneity_score nicht der Fall: Beide sind durch die Beziehung begrenzt

homogeneity_score(a, b) == completeness_score(b, a)

Vorteile

• Begrenzte Scores: 0,0 ist so schlecht wie möglich, 1,0 ist ein perfekter Score.

• Intuitive Interpretation: Ein Clustering mit schlechter V-Messung kann qualitativ in Bezug auf Homogenität und Vollständigkeit analysiert werden, um besser zu verstehen, welche "Art" von Fehlern die Zuordnung macht.

• Es werden keine Annahmen über die Clusterstruktur getroffen: Kann verwendet werden, um Clustering-Algorithmen wie k-means, die isotrope Kugelformen annehmen, mit Ergebnissen von spektralen Clustering-Algorithmen zu vergleichen, die Cluster mit „gefalteten“ Formen finden können.

Nachteile

• Die zuvor eingeführten Metriken sind nicht normalisiert in Bezug auf zufällige Beschriftungen: Das bedeutet, dass je nach Anzahl der Stichproben, Cluster und Ground-Truth-Klassen eine völlig zufällige Beschriftung nicht immer die gleichen Werte für Homogenität, Vollständigkeit und damit V-Messung ergibt. Insbesondere zufällige Beschriftungen ergeben nicht immer Null-Scores, insbesondere wenn die Anzahl der Cluster groß ist.

  Dieses Problem kann sicher ignoriert werden, wenn die Anzahl der Stichproben mehr als tausend beträgt und die Anzahl der Cluster weniger als 10 ist. Bei kleineren Stichprobengrößen oder einer größeren Anzahl von Clustern ist es sicherer, einen angepassten Index wie den Adjusted Rand Index (ARI) zu verwenden.

• Diese Metriken erfordern die Kenntnis der Ground-Truth-Klassen, die in der Praxis fast nie verfügbar sind oder eine manuelle Zuweisung durch menschliche Annotatoren erfordern (wie im überwachten Lernsetting).

Beispiele

• Anpassung für Zufälligkeit bei der Bewertung der Clustering-Leistung: Analyse des Einflusses der Datensatzgröße auf den Wert von Clustering-Metriken für zufällige Zuweisungen.

Mathematische Formulierung

Homogenitäts- und Vollständigkeits-Scores sind formal gegeben durch

\[h = 1 - \frac{H(C|K)}{H(C)}\]

\[c = 1 - \frac{H(K|C)}{H(K)}\]

wobei \(H(C|K)\) die bedingte Entropie der Klassen gegeben die Cluster-Zuordnungen ist und gegeben ist durch

\[H(C|K) = - \sum_{c=1}^{|C|} \sum_{k=1}^{|K|} \frac{n_{c,k}}{n} \cdot \log\left(\frac{n_{c,k}}{n_k}\right)\]

und \(H(C)\) die Entropie der Klassen ist und gegeben ist durch

\[H(C) = - \sum_{c=1}^{|C|} \frac{n_c}{n} \cdot \log\left(\frac{n_c}{n}\right)\]

mit \(n\) der Gesamtzahl der Stichproben, \(n_c\) und \(n_k\) der Anzahl der Stichproben, die jeweils zur Klasse \(c\) und zum Cluster \(k\) gehören, und schließlich \(n_{c,k}\) der Anzahl der Stichproben aus Klasse \(c\), die dem Cluster \(k\) zugeordnet sind.

Die bedingte Entropie der Cluster gegeben die Klasse \(H(K|C)\) und die Entropie der Cluster \(H(K)\) sind symmetrisch definiert.

Rosenberg und Hirschberg definieren die V-Messung weiter als das harmonische Mittel von Homogenität und Vollständigkeit.

\[v = 2 \cdot \frac{h \cdot c}{h + c}\]

Referenzen

• V-Measure: A conditional entropy-based external cluster evaluation measure Andrew Rosenberg und Julia Hirschberg, 2007

[B2011]

Identification and Characterization of Events in Social Media, Hila Becker, PhD-Arbeit.

2.3.11.4. Fowlkes-Mallows-Scores

Der ursprüngliche Fowlkes-Mallows-Index (FMI) sollte die Ähnlichkeit zwischen zwei Clustering-Ergebnissen messen, was inhärent ein unüberwachter Vergleich ist. Die überwachte Anpassung des Fowlkes-Mallows-Index (wie in sklearn.metrics.fowlkes_mallows_score implementiert) kann verwendet werden, wenn die Ground-Truth-Klassenzuordnungen der Stichproben bekannt sind. Der FMI ist definiert als das geometrische Mittel von paarweisem Precision und Recall.

\[\text{FMI} = \frac{\text{TP}}{\sqrt{(\text{TP} + \text{FP}) (\text{TP} + \text{FN})}}\]

In der obigen Formel

• TP (True Positive): Die Anzahl der Punktepaare, die sowohl in den wahren Labels als auch in den vorhergesagten Labels zusammen geclustert sind.

• FP (False Positive): Die Anzahl der Punktepaare, die in den vorhergesagten Labels zusammen geclustert sind, aber nicht in den wahren Labels.

• FN (False Negative): Die Anzahl der Punktepaare, die in den wahren Labels zusammen geclustert sind, aber nicht in den vorhergesagten Labels.

Der Score reicht von 0 bis 1. Ein hoher Wert zeigt eine gute Ähnlichkeit zwischen zwei Clustern an.

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140

Man kann 0 und 1 in den vorhergesagten Labels vertauschen, 2 in 3 umbenennen und denselben Score erhalten.

>>> labels_pred = [1, 1, 0, 0, 3, 3]

>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140

Perfekte Beschriftung wird mit 1,0 bewertet.

>>> labels_pred = labels_true[:]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
1.0

Schlechte (z. B. unabhängige Beschriftungen) haben Null-Scores.

>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.0

Vorteile

• Zufällige (uniforme) Beschriftungszuweisungen haben einen FMI-Score nahe 0,0 für jeden Wert von n_clusters und n_samples (was nicht der Fall ist für Mutual Information oder die V-Messung, zum Beispiel).

• Nach oben auf 1 begrenzt: Werte nahe Null zeigen zwei Beschriftungszuordnungen an, die weitgehend unabhängig sind, während Werte nahe eins eine signifikante Übereinstimmung anzeigen. Weiterhin zeigen Werte von exakt 0 rein unabhängige Beschriftungszuordnungen an, und ein FMI von exakt 1 zeigt an, dass die beiden Beschriftungszuordnungen gleich sind (mit oder ohne Permutation).

• Es werden keine Annahmen über die Clusterstruktur getroffen: Kann verwendet werden, um Clustering-Algorithmen wie k-means, die isotrope Kugelformen annehmen, mit Ergebnissen von spektralen Clustering-Algorithmen zu vergleichen, die Cluster mit „gefalteten“ Formen finden können.

Nachteile

• Im Gegensatz zu Inertia erfordern FMI-basierte Maße die Kenntnis der Ground-Truth-Klassen, die in der Praxis fast nie verfügbar sind oder eine manuelle Zuweisung durch menschliche Annotatoren erfordern (wie im überwachten Lernsetting).

Referenzen

• E. B. Fowkles und C. L. Mallows, 1983. „A method for comparing two hierarchical clusterings“. Journal of the American Statistical Association. https://www.tandfonline.com/doi/abs/10.1080/01621459.1983.10478008

• Wikipedia-Eintrag für den Fowlkes-Mallows-Index

2.3.11.5. Silhouette-Koeffizient

Wenn die Ground-Truth-Labels nicht bekannt sind, muss die Bewertung anhand des Modells selbst erfolgen. Der Silhouette-Koeffizient (sklearn.metrics.silhouette_score) ist ein Beispiel für eine solche Bewertung, bei der ein höherer Silhouette-Koeffizient-Score auf ein Modell mit besser definierten Clustern hinweist. Der Silhouette-Koeffizient wird für jede Stichprobe berechnet und besteht aus zwei Scores.

• a: Der mittlere Abstand zwischen einer Stichprobe und allen anderen Punkten in derselben Klasse.

• b: Der mittlere Abstand zwischen einer Stichprobe und allen anderen Punkten im nächstgelegenen Cluster.

Der Silhouette-Koeffizient s für eine einzelne Stichprobe ist dann gegeben durch

\[s = \frac{b - a}{max(a, b)}\]

Der Silhouette-Koeffizient für eine Menge von Stichproben ist der Mittelwert des Silhouette-Koeffizienten für jede Stichprobe.

>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)

Im normalen Gebrauch wird der Silhouette-Koeffizient auf die Ergebnisse einer Clusteranalyse angewendet.

>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.silhouette_score(X, labels, metric='euclidean')
0.55

Vorteile

• Der Score ist zwischen -1 für eine falsche Clusterbildung und +1 für eine stark dichte Clusterbildung begrenzt. Scores um Null herum deuten auf überlappende Cluster hin.

• Der Score ist höher, wenn Cluster dicht und gut getrennt sind, was mit einem Standardkonzept eines Clusters zusammenhängt.

Nachteile

• Der Silhouette-Koeffizient ist im Allgemeinen für konvexe Cluster höher als für andere Clusterkonzepte, wie z. B. dichte-basierte Cluster, die durch DBSCAN erhalten werden.

Beispiele

• Auswahl der Anzahl von Clustern mit Silhouettenanalyse bei KMeans-Clustering : In diesem Beispiel wird die Silhouettenanalyse verwendet, um einen optimalen Wert für n_clusters auszuwählen.

Referenzen

• Peter J. Rousseeuw (1987). „Silhouettes: a Graphical Aid to the Interpretation and Validation of Cluster Analysis“. Computational and Applied Mathematics 20: 53-65.

2.3.11.6. Calinski-Harabasz-Index

Wenn die Ground-Truth-Labels nicht bekannt sind, kann der Calinski-Harabasz-Index (sklearn.metrics.calinski_harabasz_score) – auch bekannt als Varianzverhältnis-Kriterium – zur Bewertung des Modells verwendet werden, wobei ein höherer Calinski-Harabasz-Score auf ein Modell mit besser definierten Clustern hinweist.

Der Index ist das Verhältnis der Summe der Streuung zwischen den Clustern und der Streuung innerhalb der Cluster für alle Cluster (wobei Streuung als Summe der quadrierten Abstände definiert ist).

>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)

Im normalen Gebrauch wird der Calinski-Harabasz-Index auf die Ergebnisse einer Clusteranalyse angewendet.

>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.calinski_harabasz_score(X, labels)
561.59

Vorteile

• Der Score ist höher, wenn Cluster dicht und gut getrennt sind, was mit einem Standardkonzept eines Clusters zusammenhängt.

• Die Berechnung des Scores ist schnell.

Nachteile

• Der Calinski-Harabasz-Index ist im Allgemeinen für konvexe Cluster höher als für andere Clusterkonzepte, wie z. B. dichte-basierte Cluster, die durch DBSCAN erhalten werden.

Mathematische Formulierung

Für eine Menge von Daten \(E\) der Größe \(n_E\), die in \(k\) Cluster geclustert wurde, ist der Calinski-Harabasz-Score \(s\) definiert als das Verhältnis des Mittelwerts der Streuung zwischen den Clustern und der Streuung innerhalb der Cluster.

\[s = \frac{\mathrm{tr}(B_k)}{\mathrm{tr}(W_k)} \times \frac{n_E - k}{k - 1}\]

wobei \(\mathrm{tr}(B_k)\) die Spur der Matrix der Streuung zwischen den Gruppen und \(\mathrm{tr}(W_k)\) die Spur der Matrix der Streuung innerhalb der Cluster ist, definiert durch

\[W_k = \sum_{q=1}^k \sum_{x \in C_q} (x - c_q) (x - c_q)^T\]

\[B_k = \sum_{q=1}^k n_q (c_q - c_E) (c_q - c_E)^T\]

mit \(C_q\) die Menge der Punkte im Cluster \(q\), \(c_q\) das Zentrum des Clusters \(q\), \(c_E\) das Zentrum von \(E\) und \(n_q\) die Anzahl der Punkte im Cluster \(q\).

Referenzen

• Caliński, T., & Harabasz, J. (1974). „A Dendrite Method for Cluster Analysis“. Communications in Statistics-theory and Methods 3: 1-27.

2.3.11.7. Davies-Bouldin-Index

Wenn die Ground-Truth-Labels nicht bekannt sind, kann der Davies-Bouldin-Index (sklearn.metrics.davies_bouldin_score) zur Bewertung des Modells verwendet werden, wobei ein niedrigerer Davies-Bouldin-Index auf ein Modell mit besserer Trennung zwischen den Clustern hinweist.

Dieser Index bezeichnet die durchschnittliche „Ähnlichkeit“ zwischen Clustern, wobei die Ähnlichkeit ein Maß ist, das den Abstand zwischen den Clustern mit der Größe der Cluster selbst vergleicht.

Null ist der niedrigste mögliche Score. Werte näher an Null deuten auf eine bessere Partition hin.

Im normalen Gebrauch wird der Davies-Bouldin-Index auf die Ergebnisse einer Clusteranalyse angewendet wie folgt:

>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> X = iris.data
>>> from sklearn.cluster import KMeans
>>> from sklearn.metrics import davies_bouldin_score
>>> kmeans = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans.labels_
>>> davies_bouldin_score(X, labels)
0.666

Vorteile

• Die Berechnung von Davies-Bouldin ist einfacher als die von Silhouette-Scores.

• Der Index basiert ausschließlich auf Mengen und Merkmalen, die dem Datensatz eigen sind, da seine Berechnung nur punktweise Abstände verwendet.

Nachteile

• Der Davies-Bouldin-Index ist im Allgemeinen für konvexe Cluster höher als für andere Clusterkonzepte, wie z. B. dichte-basierte Cluster, die aus DBSCAN erhalten werden.

• Die Verwendung der Zentroid-Entfernungen beschränkt die Distanzmetrik auf den euklidischen Raum.

Mathematische Formulierung

Der Index ist definiert als die durchschnittliche Ähnlichkeit zwischen jedem Cluster \(C_i\) für \(i=1, ..., k\) und seinem ähnlichsten Cluster \(C_j\). Im Kontext dieses Index ist die Ähnlichkeit definiert als ein Maß \(R_{ij}\), das abwägt

• \(s_i\), der mittlere Abstand zwischen jedem Punkt des Clusters \(i\) und dem Zentrum dieses Clusters – auch bekannt als Kleindurchmesser.

• \(d_{ij}\), der Abstand zwischen den Cluster-Zentren \(i\) und \(j\).

Eine einfache Wahl zur Konstruktion von \(R_{ij}\), so dass sie nicht-negativ und symmetrisch ist, ist

\[R_{ij} = \frac{s_i + s_j}{d_{ij}}\]

Dann ist der Davies-Bouldin-Index definiert als

\[DB = \frac{1}{k} \sum_{i=1}^k \max_{i \neq j} R_{ij}\]

Referenzen

• Davies, David L.; Bouldin, Donald W. (1979). „A Cluster Separation Measure“ IEEE Transactions on Pattern Analysis and Machine Intelligence. PAMI-1 (2): 224-227.

• Halkidi, Maria; Batistakis, Yannis; Vazirgiannis, Michalis (2001). „On Clustering Validation Techniques“ Journal of Intelligent Information Systems, 17(2-3), 107-145.

• Wikipedia-Eintrag für den Davies-Bouldin-Index.

2.3.11.8. Kontingenzmatrix

Die Kontingenzmatrix (sklearn.metrics.cluster.contingency_matrix) gibt die Schnittkardinalität für jedes Paar von wahren/vorhergesagten Clustern an. Die Kontingenzmatrix liefert hinreichende Statistiken für alle Clustering-Metriken, bei denen die Stichproben unabhängig und identisch verteilt sind und keine Instanzen, die nicht geclustert wurden, berücksichtigt werden müssen.

Hier ist ein Beispiel:

>>> from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
       [0, 1, 2]])

Die erste Zeile der Ausgabe zeigt, dass es drei Stichproben gibt, deren wahres Cluster „a“ ist. Davon sind zwei im vorhergesagten Cluster 0, eine im Cluster 1 und keine im Cluster 2. Und die zweite Zeile zeigt, dass es drei Stichproben gibt, deren wahres Cluster „b“ ist. Davon ist keine im vorhergesagten Cluster 0, eine im Cluster 1 und zwei im Cluster 2.

Eine Konfusionsmatrix für die Klassifizierung ist eine quadratische Kontingenzmatrix, bei der die Reihenfolge der Zeilen und Spalten einer Liste von Klassen entspricht.

Vorteile

• Ermöglicht die Untersuchung der Verteilung jedes wahren Clusters über die vorhergesagten Cluster und umgekehrt.

• Die berechnete Kontingenztafel wird typischerweise zur Berechnung einer Ähnlichkeitsstatistik (wie die anderen in diesem Dokument aufgeführten) zwischen den beiden Clustern verwendet.

Nachteile

• Die Kontingenzmatrix ist bei einer kleinen Anzahl von Clustern leicht zu interpretieren, wird aber bei einer großen Anzahl von Clustern sehr schwer zu interpretieren.

• Sie liefert keine einzelne Metrik, die als Optimierungsziel für das Clustering verwendet werden kann.

Referenzen

• Wikipedia-Eintrag für Kontingenzmatrix

2.3.11.9. Paarkonfusionsmatrix

Die Paarkonfusionsmatrix (sklearn.metrics.cluster.pair_confusion_matrix) ist eine 2x2-Ähnlichkeitsmatrix.

\[\begin{split}C = \left[\begin{matrix} C_{00} & C_{01} \\ C_{10} & C_{11} \end{matrix}\right]\end{split}\]

zwischen zwei Clustern, berechnet durch die Betrachtung aller Stichprobenpaare und das Zählen von Paaren, die sowohl in den wahren als auch in den vorhergesagten Clustern in denselben oder in verschiedene Cluster zugeordnet werden.

Sie hat folgende Einträge:

\(C_{00}\) : Anzahl der Paare, bei denen beide Clusterzuordnungen die Stichproben nicht zusammen gruppieren.

\(C_{10}\) : Anzahl der Paare, bei denen die wahre Label-Clusterung die Stichproben gruppiert, aber die andere Clusterung die Stichproben nicht gruppiert.

\(C_{01}\) : Anzahl der Paare, bei denen die wahre Label-Clusterung die Stichproben nicht gruppiert, aber die andere Clusterung die Stichproben gruppiert.

\(C_{11}\) : Anzahl der Paare, bei denen beide Clusterzuordnungen die Stichproben zusammen gruppieren.

Wenn ein Paar von Stichproben, das zusammen gruppiert wird, als positives Paar betrachtet wird, dann sind, wie in der binären Klassifizierung, die Anzahl der wahren Negativen \(C_{00}\), der falsch Negativen \(C_{10}\), der wahren Positiven \(C_{11}\) und der falsch Positiven \(C_{01}\).

Perfekt übereinstimmende Labels haben alle nicht-null Einträge auf der Diagonalen, unabhängig von den tatsächlichen Label-Werten.

>>> from sklearn.metrics.cluster import pair_confusion_matrix
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 1])
array([[8, 0],
       [0, 4]])

>>> pair_confusion_matrix([0, 0, 1, 1], [1, 1, 0, 0])
array([[8, 0],
       [0, 4]])

Labels, die alle Klassenmitglieder demselben Cluster zuordnen, sind vollständig, können aber nicht immer rein sein, werden daher bestraft und weisen einige nicht-diagonale Einträge ungleich Null auf.

>>> pair_confusion_matrix([0, 0, 1, 2], [0, 0, 1, 1])
array([[8, 2],
       [0, 2]])

Die Matrix ist nicht symmetrisch.

>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 2])
array([[8, 0],
       [2, 2]])

Wenn Klassenmitglieder vollständig über verschiedene Cluster aufgeteilt sind, ist die Zuordnung völlig unvollständig, daher hat die Matrix alle diagonalen Einträge gleich Null.

>>> pair_confusion_matrix([0, 0, 0, 0], [0, 1, 2, 3])
array([[ 0,  0],
       [12,  0]])

Referenzen

• „Comparing Partitions“ L. Hubert und P. Arabie, Journal of Classification 1985