2.4. Biclustering#
Biclustering-Algorithmen gruppieren gleichzeitig Zeilen und Spalten einer Datenmatrix. Diese Gruppen von Zeilen und Spalten werden als Bicluster bezeichnet. Jeder Bicluster definiert eine Untermatrix der ursprünglichen Datenmatrix mit bestimmten gewünschten Eigenschaften.
Beispielsweise kann bei einer Matrix der Form (10, 10) ein mögliches Bicluster mit drei Zeilen und zwei Spalten eine Untermatrix der Form (3, 2) definieren.
>>> import numpy as np
>>> data = np.arange(100).reshape(10, 10)
>>> rows = np.array([0, 2, 3])[:, np.newaxis]
>>> columns = np.array([1, 2])
>>> data[rows, columns]
array([[ 1, 2],
[21, 22],
[31, 32]])
Zu Visualisierungszwecken können die Zeilen und Spalten der Datenmatrix, gegeben ein Bicluster, neu angeordnet werden, um das Bicluster zusammenhängend darzustellen.
Die Algorithmen unterscheiden sich darin, wie sie Bicluster definieren. Einige gängige Typen sind:
konstante Werte, konstante Zeilen oder konstante Spalten
ungewöhnlich hohe oder niedrige Werte
Untermatrizen mit geringer Varianz
korrelierte Zeilen oder Spalten
Die Algorithmen unterscheiden sich auch darin, wie Zeilen und Spalten Biclustern zugeordnet werden können, was zu unterschiedlichen Bicluster-Strukturen führt. Blockdiagonale oder schachbrettartige Strukturen entstehen, wenn Zeilen und Spalten in Partitionen aufgeteilt werden.
Wenn jede Zeile und jede Spalte zu genau einem Bicluster gehört, enthüllt die Neuanordnung der Zeilen und Spalten der Datenmatrix die Bicluster auf der Diagonalen. Hier ist ein Beispiel für diese Struktur, bei der Bicluster höhere Durchschnittswerte aufweisen als die anderen Zeilen und Spalten.
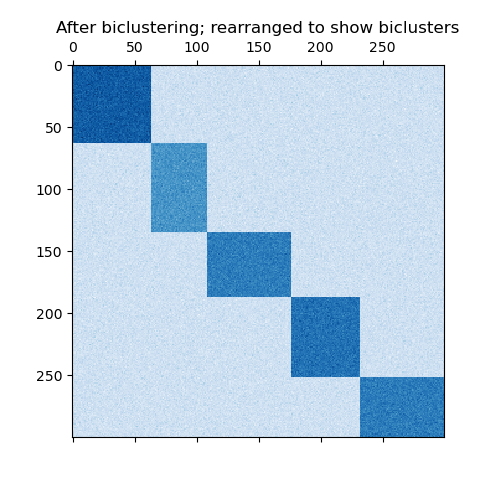
Ein Beispiel für durch Partitionierung von Zeilen und Spalten gebildete Bicluster.#
Im Schachbrettfall gehört jede Zeile zu allen Spaltenclustern und jede Spalte zu allen Zeilenclustern. Hier ist ein Beispiel für diese Struktur, bei der die Varianz der Werte innerhalb jedes Biclusters gering ist.
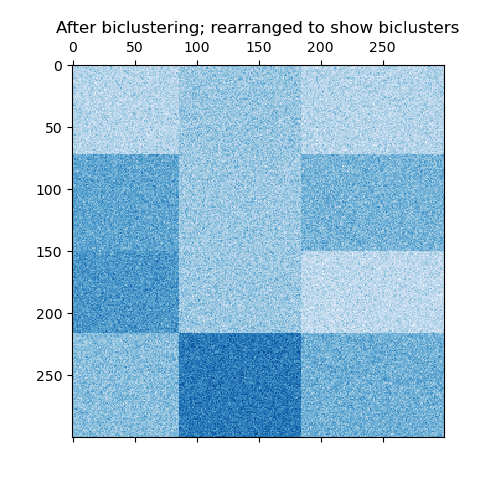
Ein Beispiel für schachbrettartige Bicluster.#
Nach dem Trainieren eines Modells können die Mitgliedschaften der Zeilen- und Spaltencluster in den Attributen rows_ und columns_ gefunden werden. rows_[i] ist ein binärer Vektor mit nicht-null Einträgen, die Zeilen entsprechen, die zum Bicluster i gehören. Ähnlich gibt columns_[i] an, welche Spalten zum Bicluster i gehören.
Einige Modelle verfügen auch über die Attribute row_labels_ und column_labels_. Diese Modelle partitionieren die Zeilen und Spalten, wie bei den blockdiagonalen und schachbrettartigen Bicluster-Strukturen.
Hinweis
Biclustering hat in verschiedenen Bereichen viele andere Namen, darunter Co-Clustering, Two-Mode-Clustering, Two-Way-Clustering, Block-Clustering, Coupled Two-Way-Clustering usw. Die Namen einiger Algorithmen, wie z. B. der Spectral Co-Clustering-Algorithmus, spiegeln diese alternativen Namen wider.
2.4.1. Spectral Co-Clustering#
Der Algorithmus SpectralCoclustering findet Bicluster mit Werten, die höher sind als die in den entsprechenden anderen Zeilen und Spalten. Jede Zeile und jede Spalte gehört zu genau einem Bicluster, sodass die Neuanordnung der Zeilen und Spalten zur Darstellung zusammenhängender Partitionen diese hohen Werte entlang der Diagonalen offenbart.
Hinweis
Der Algorithmus behandelt die Eingabedatenmatrix als bipartiten Graphen: Die Zeilen und Spalten der Matrix entsprechen den beiden Mengen von Knoten, und jeder Eintrag entspricht einer Kante zwischen einer Zeile und einer Spalte. Der Algorithmus approximiert den normalisierten Schnitt dieses Graphen, um starke Teilgraphen zu finden.
2.4.1.1. Mathematische Formulierung#
Eine Annäherungslösung für den optimalen normalisierten Schnitt kann durch die verallgemeinerte Eigenwertzerlegung des Laplace-Operators des Graphen gefunden werden. Normalerweise würde dies bedeuten, direkt mit der Laplace-Matrix zu arbeiten. Wenn die ursprüngliche Datenmatrix \(A\) die Form \(m \times n\) hat, hat die Laplace-Matrix für den entsprechenden bipartiten Graphen die Form \((m + n) \times (m + n)\). In diesem Fall ist es jedoch möglich, direkt mit \(A\) zu arbeiten, was kleiner und effizienter ist.
Die Eingabematrix \(A\) wird wie folgt vorverarbeitet:
Dabei ist \(R\) die Diagonalmatrix, bei der der Eintrag \(i\) gleich \(\sum_{j} A_{ij}\) ist, und \(C\) ist die Diagonalmatrix, bei der der Eintrag \(j\) gleich \(\sum_{i} A_{ij}\) ist.
Die Singulärwertzerlegung \(A_n = U \Sigma V^\top\) liefert die Partitionen der Zeilen und Spalten von \(A\). Eine Teilmenge der linken Singulärvektoren liefert die Zeilenpartitionen, und eine Teilmenge der rechten Singulärvektoren liefert die Spaltenpartitionen.
Die \(\ell = \lceil \log_2 k \rceil\) Singulärvektoren, beginnend mit dem zweiten, liefern die gewünschten Partitionierungsinformationen. Sie werden zur Bildung der Matrix \(Z\) verwendet:
wobei die Spalten von \(U\) \(u_2, \dots, u_{\ell + 1}\) sind, und ähnlich für \(V\).
Anschließend werden die Zeilen von \(Z\) mit k-means gruppiert. Die ersten n_rows Labels ergeben die Zeilenpartitionierung, und die restlichen n_columns Labels ergeben die Spaltenpartitionierung.
Beispiele
Eine Demo des Spectral Co-Clustering-Algorithmus: Ein einfaches Beispiel, das zeigt, wie eine Datenmatrix mit Biclustern generiert und diese Methode darauf angewendet wird.
Biclustering von Dokumenten mit dem Spectral Co-Clustering-Algorithmus: Ein Beispiel für die Suche nach Biclustern im Twenty Newsgroup-Datensatz.
Referenzen
Dhillon, Inderjit S, 2001. Co-clustering documents and words using bipartite spectral graph partitioning
2.4.2. Spectral Biclustering#
Der Algorithmus SpectralBiclustering geht davon aus, dass die Eingabedatenmatrix eine verborgene schachbrettartige Struktur aufweist. Die Zeilen und Spalten einer Matrix mit dieser Struktur können so partitioniert werden, dass die Einträge eines beliebigen Biclusters im kartesischen Produkt von Zeilenclustern und Spaltenclustern annähernd konstant sind. Wenn es beispielsweise zwei Zeilenpartitionen und drei Spaltenpartitionen gibt, gehört jede Zeile zu drei Biclustern und jede Spalte zu zwei Biclustern.
Der Algorithmus partitioniert die Zeilen und Spalten einer Matrix so, dass eine entsprechende blockweise konstante schachbrettartige Matrix eine gute Approximation der ursprünglichen Matrix liefert.
2.4.2.1. Mathematische Formulierung#
Die Eingabematrix \(A\) wird zuerst normalisiert, um das schachbrettartige Muster deutlicher zu machen. Es gibt drei mögliche Methoden:
Unabhängige Zeilen- und Spaltennormalisierung, wie bei Spectral Co-Clustering. Diese Methode bewirkt, dass die Zeilensummen konstant sind und die Spaltensummen einen anderen konstanten Wert aufweisen.
Bistochastisierung: wiederholte Zeilen- und Spaltennormalisierung bis zur Konvergenz. Diese Methode bewirkt, dass sowohl die Zeilen- als auch die Spaltensummen konstant und gleich sind.
Log-Normalisierung: Der Logarithmus der Datenmatrix wird berechnet: \(L = \log A\). Dann werden der Spaltenmittelwert \(\overline{L_{i \cdot}}\), der Zeilenmittelwert \(\overline{L_{\cdot j}}\) und der Gesamtmittelwert \(\overline{L_{\cdot \cdot}}\) von \(L\) berechnet. Die endgültige Matrix wird gemäß der Formel berechnet:
Nach der Normalisierung werden die ersten wenigen Singulärvektoren berechnet, genau wie beim Spectral Co-Clustering-Algorithmus.
Wenn Log-Normalisierung verwendet wurde, sind alle Singulärvektoren bedeutsam. Wenn jedoch unabhängige Normalisierung oder Bistochastisierung verwendet wurden, werden die ersten Singulärvektoren \(u_1\) und \(v_1\) verworfen. Von nun an beziehen sich die "ersten" Singulärvektoren auf \(u_2 \dots u_{p+1}\) und \(v_2 \dots v_{p+1}\), außer im Fall der Log-Normalisierung.
Diese Singulärvektoren werden nach ihrer Fähigkeit, durch einen stückweise konstanten Vektor approximiert zu werden, sortiert. Die Approximation für jeden Vektor wird mittels eindimensionalem k-means gefunden und anhand der euklidischen Distanz bewertet. Eine Teilmenge der besten linken und rechten Singulärvektoren wird ausgewählt. Anschließend wird die Datenmenge auf diese beste Teilmenge von Singulärvektoren projiziert und gruppiert.
Wenn beispielsweise \(p\) Singulärvektoren berechnet wurden, werden die \(q\) besten wie beschrieben gefunden, wobei \(q<p\). Sei \(U\) die Matrix mit den \(q\) besten linken Singulärvektoren als Spalten, und analog \(V\) für die rechten. Um die Zeilen zu partitionieren, werden die Zeilen von \(A\) in einen \(q\)-dimensionalen Raum projiziert: \(A * V\). Wenn man die \(m\) Zeilen dieser \(m \times q\) Matrix als Stichproben behandelt und k-means zur Gruppierung verwendet, erhält man die Zeilenlabels. Ähnlich führt die Projektion der Spalten auf \(A^{\top} * U\) und die Gruppierung dieser \(n \times q\) Matrix zu den Spaltenlabels.
Beispiele
Eine Demo des Spectral Biclustering-Algorithmus: Ein einfaches Beispiel, das zeigt, wie eine schachbrettartige Matrix generiert und biclustert wird.
Referenzen
Kluger, Yuval, et. al., 2003. Spectral biclustering of microarray data: coclustering genes and conditions
2.4.3. Biclustering-Evaluierung#
Es gibt zwei Möglichkeiten, ein Biclustering-Ergebnis zu bewerten: intern und extern. Interne Maße, wie z. B. Clusterstabilität, beruhen nur auf den Daten und den Ergebnissen selbst. Derzeit gibt es in scikit-learn keine internen Bicluster-Maße. Externe Maße beziehen sich auf eine externe Informationsquelle, wie z. B. die wahre Lösung. Bei der Arbeit mit realen Daten ist die wahre Lösung normalerweise unbekannt, aber die Biclusterung künstlicher Daten kann zur genauen Bewertung von Algorithmen nützlich sein, da die wahre Lösung bekannt ist.
Um eine Menge gefundener Bicluster mit einer Menge wahrer Bicluster zu vergleichen, werden zwei Ähnlichkeitsmaße benötigt: ein Ähnlichkeitsmaß für einzelne Bicluster und eine Möglichkeit, diese individuellen Ähnlichkeiten zu einem Gesamtscore zu kombinieren.
Zum Vergleich einzelner Bicluster wurden mehrere Maße verwendet. Derzeit ist nur der Jaccard-Index implementiert:
wobei \(A\) und \(B\) Bicluster sind, \(|A \cap B|\) die Anzahl der Elemente in ihrer Schnittmenge ist. Der Jaccard-Index erreicht sein Minimum von 0, wenn die Bicluster überhaupt nicht überlappen, und sein Maximum von 1, wenn sie identisch sind.
Mehrere Methoden wurden entwickelt, um zwei Sätze von Biclustern zu vergleichen. Derzeit ist nur consensus_score (Hochreiter et. al., 2010) verfügbar.
Berechnet Bicluster-Ähnlichkeiten für Paare von Biclustern, eines aus jedem Satz, unter Verwendung des Jaccard-Index oder eines ähnlichen Maßes.
Weist Bicluster aus einem Satz einem anderen Satz in einer Eins-zu-Eins-Zuordnung zu, um die Summe ihrer Ähnlichkeiten zu maximieren. Dieser Schritt wird mit
scipy.optimize.linear_sum_assignmentdurchgeführt, die einen modifizierten Jonker-Volgenant-Algorithmus verwendet.Die endgültige Summe der Ähnlichkeiten wird durch die Größe des größeren Satzes geteilt.
Der minimale Konsens-Score von 0 tritt auf, wenn alle Paare von Biclustern völlig unähnlich sind. Der maximale Score von 1 tritt auf, wenn beide Sätze identisch sind.
Referenzen
Hochreiter, Bodenhofer, et. al., 2010. FABIA: factor analysis for bicluster acquisition.