2.7. Neuheits- und Ausreißererkennung#
Viele Anwendungen erfordern die Fähigkeit zu entscheiden, ob eine neue Beobachtung zur gleichen Verteilung wie bestehende Beobachtungen gehört (sie ist ein Inlier) oder als unterschiedlich betrachtet werden sollte (sie ist ein Outlier). Oft wird diese Fähigkeit zur Bereinigung realer Datensätze verwendet. Zwei wichtige Unterscheidungen müssen getroffen werden:
- Ausreißererkennung:
Die Trainingsdaten enthalten Ausreißer, die als Beobachtungen definiert sind, die weit von den anderen entfernt sind. Ausreißererkennungs-Estimators versuchen somit, die Regionen anzupassen, in denen die Trainingsdaten am dichtesten konzentriert sind, und ignorieren dabei die abweichenden Beobachtungen.
- Neuheitserkennung:
Die Trainingsdaten sind nicht mit Ausreißern verunreinigt, und wir sind daran interessiert, festzustellen, ob eine **neue** Beobachtung ein Ausreißer ist. In diesem Kontext wird ein Ausreißer auch als Neuheit bezeichnet.
Ausreißererkennung und Neuheitserkennung werden beide zur Anomalieerkennung verwendet, bei der man daran interessiert ist, anormale oder ungewöhnliche Beobachtungen zu erkennen. Ausreißererkennung wird dann auch als unüberwachte Anomalieerkennung und Neuheitserkennung als semi-überwachte Anomalieerkennung bezeichnet. Im Kontext der Ausreißererkennung können die Ausreißer/Anomalien keinen dichten Cluster bilden, da verfügbare Estimators davon ausgehen, dass die Ausreißer/Anomalien sich in Regionen mit geringer Dichte befinden. Im Gegensatz dazu können im Kontext der Neuheitserkennung Neuheiten/Anomalien einen dichten Cluster bilden, solange sie sich in einer Region mit geringer Dichte der Trainingsdaten befinden, die in diesem Kontext als normal betrachtet wird.
Das scikit-learn-Projekt stellt eine Reihe von Werkzeugen für maschinelles Lernen zur Verfügung, die sowohl für die Neuheits- als auch für die Ausreißererkennung verwendet werden können. Diese Strategie wird mit Objekten implementiert, die auf unüberwachte Weise aus den Daten lernen.
estimator.fit(X_train)
neue Beobachtungen können dann mit einer predict-Methode als Inlier oder Outlier sortiert werden.
estimator.predict(X_test)
Inlier werden mit 1 und Ausreißer mit -1 gekennzeichnet. Die predict-Methode verwendet einen Schwellenwert für die vom Estimator berechnete rohe Scoring-Funktion. Diese Scoring-Funktion ist über die score_samples-Methode zugänglich, während der Schwellenwert durch den Parameter contamination gesteuert werden kann.
Die Methode decision_function wird ebenfalls aus der Scoring-Funktion abgeleitet, so dass negative Werte Ausreißer und nicht-negative Werte Inlier sind.
estimator.decision_function(X_test)
Beachten Sie, dass neighbors.LocalOutlierFactor standardmäßig keine predict, decision_function und score_samples-Methoden unterstützt, sondern nur eine fit_predict-Methode, da dieser Estimator ursprünglich für die Ausreißererkennung gedacht war. Die Scores der Abnormalität der Trainingsstichproben sind über das Attribut negative_outlier_factor_ zugänglich.
Wenn Sie neighbors.LocalOutlierFactor tatsächlich für die Neuheitserkennung verwenden möchten, d.h. um Labels vorherzusagen oder den Score der Abnormalität neuer, ungesehener Daten zu berechnen, können Sie den Estimator mit dem Parameter novelty auf True setzen, bevor Sie den Estimator fitten. In diesem Fall ist fit_predict nicht verfügbar.
Warnung
Neuheitserkennung mit Local Outlier Factor
Wenn novelty auf True gesetzt ist, beachten Sie, dass Sie predict, decision_function und score_samples nur auf neuen, ungesehenen Daten verwenden dürfen und nicht auf den Trainingsstichproben, da dies zu falschen Ergebnissen führen würde. D.h., das Ergebnis von predict wird nicht dasselbe sein wie das von fit_predict. Die Scores der Abnormalität der Trainingsstichproben sind immer über das Attribut negative_outlier_factor_ zugänglich.
Das Verhalten von neighbors.LocalOutlierFactor wird in der folgenden Tabelle zusammengefasst.
Methode |
Ausreißererkennung |
Neuheitserkennung |
|---|---|---|
|
OK |
Nicht verfügbar |
|
Nicht verfügbar |
Nur auf neue Daten anwenden |
|
Nicht verfügbar |
Nur auf neue Daten anwenden |
|
Verwenden Sie |
Nur auf neue Daten anwenden |
|
OK |
OK |
2.7.1. Überblick über Ausreißererkennungsmethoden#
Ein Vergleich der Ausreißererkennungsalgorithmen in scikit-learn. Local Outlier Factor (LOF) zeigt keine Entscheidungsgrenze in Schwarz an, da es keine predict-Methode gibt, die auf neue Daten angewendet werden kann, wenn es zur Ausreißererkennung verwendet wird.
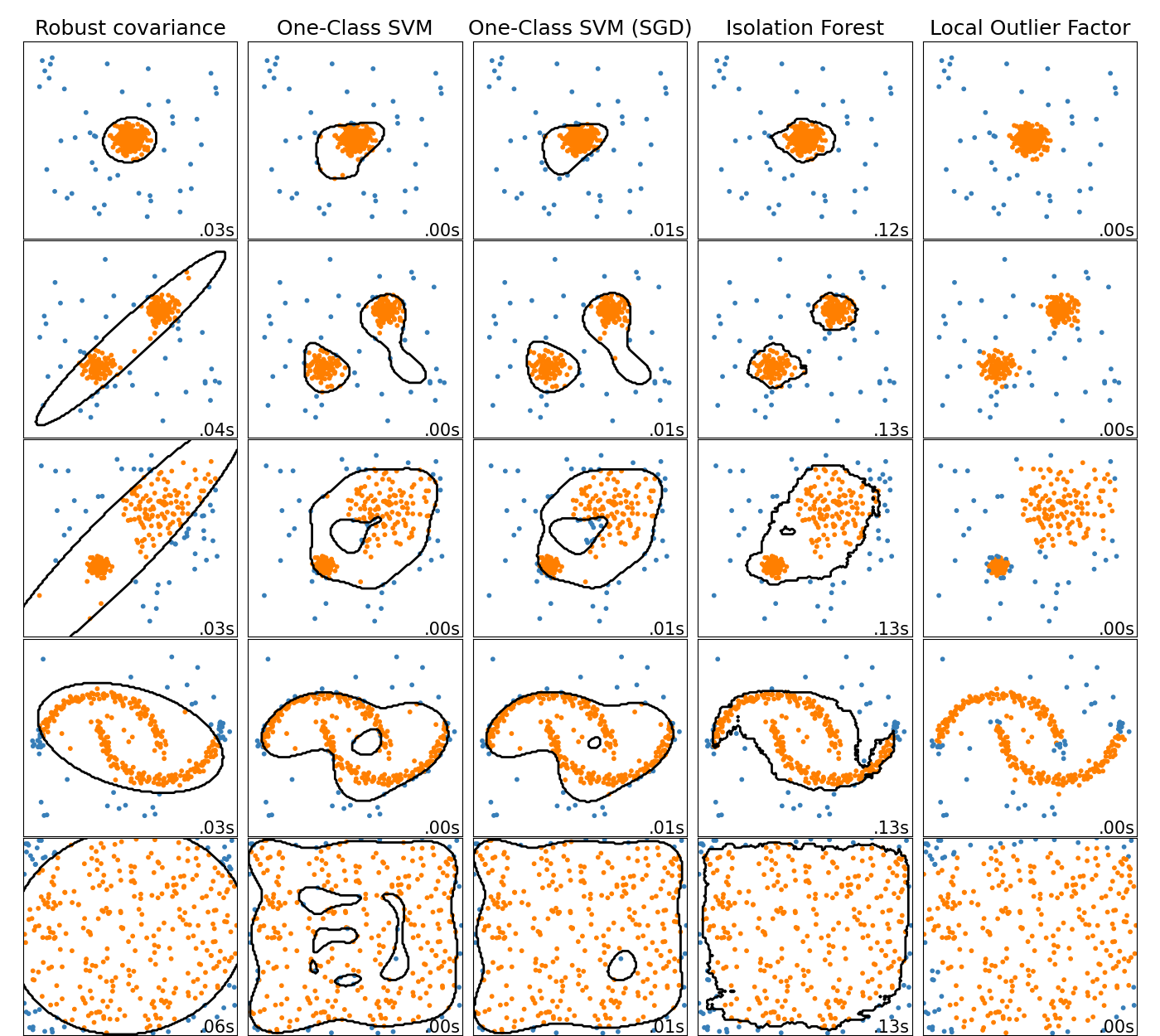
ensemble.IsolationForest und neighbors.LocalOutlierFactor schneiden auf den betrachteten Datensätzen vernünftig ab. Das svm.OneClassSVM ist dafür bekannt, empfindlich auf Ausreißer zu reagieren und schneidet daher bei der Ausreißererkennung nicht sehr gut ab. Dennoch ist die Ausreißererkennung in hohen Dimensionen oder ohne Annahmen über die Verteilung der Inlier-Daten sehr anspruchsvoll. svm.OneClassSVM kann immer noch mit Ausreißererkennung verwendet werden, erfordert aber eine Feinabstimmung seines Hyperparameters nu, um Ausreißer zu behandeln und Overfitting zu verhindern. linear_model.SGDOneClassSVM bietet eine Implementierung eines linearen One-Class SVM mit linearer Komplexität in Bezug auf die Anzahl der Stichproben. Diese Implementierung wird hier mit einer Kernel-Approximationstechnik verwendet, um Ergebnisse zu erzielen, die svm.OneClassSVM, das standardmäßig einen Gaußschen Kernel verwendet, ähneln. Schließlich nimmt covariance.EllipticEnvelope an, dass die Daten Gaußsch sind und lernt eine Ellipse. Weitere Details zu den verschiedenen Estimators finden Sie im Beispiel Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Spielzeugdatensätzen und in den folgenden Abschnitten.
Beispiele
Siehe Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Spielzeugdatensätzen für einen Vergleich von
svm.OneClassSVM,ensemble.IsolationForest,neighbors.LocalOutlierFactorundcovariance.EllipticEnvelope.Siehe Bewertung von Ausreißererkennungs-Estimators für ein Beispiel, das zeigt, wie Ausreißererkennungs-Estimators,
neighbors.LocalOutlierFactorundensemble.IsolationForestmithilfe von ROC-Kurven ausmetrics.RocCurveDisplaybewertet werden.
2.7.2. Neuheitserkennung#
Betrachten Sie einen Datensatz von \(n\) Beobachtungen aus derselben Verteilung, die durch \(p\) Merkmale beschrieben wird. Stellen Sie sich nun vor, wir fügen diesem Datensatz eine weitere Beobachtung hinzu. Ist die neue Beobachtung so anders als die anderen, dass wir bezweifeln können, dass sie regelmäßig ist? (d.h. stammt sie aus derselben Verteilung?) Oder ist sie im Gegenteil so ähnlich zu den anderen, dass wir sie von den ursprünglichen Beobachtungen nicht unterscheiden können? Dies ist die Frage, die von den Werkzeugen und Methoden der Neuheitserkennung behandelt wird.
Im Allgemeinen geht es darum, eine grobe, nahe Grenze zu lernen, die die Kontur der Verteilung der ursprünglichen Beobachtungen im \(p\)-dimensionalen Einbettungsraum abgrenzt. Wenn sich dann weitere Beobachtungen innerhalb des grenzdefinierten Unterraums befinden, werden sie als aus derselben Population wie die ursprünglichen Beobachtungen stammend betrachtet. Andernfalls, wenn sie außerhalb der Grenze liegen, können wir mit einer bestimmten Sicherheit sagen, dass sie abnormal sind.
Der One-Class SVM wurde von Schölkopf et al. zu diesem Zweck eingeführt und im Modul Support Vector Machines im Objekt svm.OneClassSVM implementiert. Er erfordert die Wahl eines Kernels und eines skalaren Parameters zur Definition einer Grenze. Der RBF-Kernel wird üblicherweise gewählt, obwohl es keine exakte Formel oder keinen Algorithmus gibt, um seinen Bandbreitenparameter festzulegen. Dies ist der Standard in der scikit-learn-Implementierung. Der Parameter nu, auch bekannt als Marge des One-Class SVM, entspricht der Wahrscheinlichkeit, eine neue, aber reguläre Beobachtung außerhalb der Grenze zu finden.
Referenzen
Estimating the support of a high-dimensional distribution Schölkopf, Bernhard, et al. Neural computation 13.7 (2001): 1443-1471.
Beispiele
Siehe One-Class SVM mit nicht-linearer Kernel (RBF) zur Visualisierung der um Daten gelernten Grenze durch ein
svm.OneClassSVM-Objekt.
2.7.2.1. Skalierung des One-Class SVM#
Eine Online-Lineare Version des One-Class SVM ist in linear_model.SGDOneClassSVM implementiert. Diese Implementierung skaliert linear mit der Anzahl der Stichproben und kann mit einer Kernel-Approximation verwendet werden, um die Lösung eines kernelisierten svm.OneClassSVM zu approximieren, dessen Komplexität bestenfalls quadratisch in der Anzahl der Stichproben ist. Siehe Abschnitt Online One-Class SVM für weitere Details.
Beispiele
Siehe One-Class SVM im Vergleich zu One-Class SVM mit stochastischem Gradientenabstieg für eine Illustration der Approximation eines kernelisierten One-Class SVM mit
linear_model.SGDOneClassSVMin Kombination mit Kernel-Approximation.
2.7.3. Ausreißererkennung#
Die Ausreißererkennung ist der Neuheitserkennung ähnlich in dem Sinne, dass das Ziel darin besteht, einen Kern aus regulären Beobachtungen von einigen verunreinigenden zu trennen, die als Ausreißer bezeichnet werden. Im Falle der Ausreißererkennung haben wir jedoch keinen sauberen Datensatz, der die Population der regulären Beobachtungen darstellt und zur Schulung beliebiger Werkzeuge verwendet werden kann.
2.7.3.1. Anpassen einer elliptischen Hülle#
Eine gängige Methode zur Durchführung der Ausreißererkennung ist die Annahme, dass die regulären Daten aus einer bekannten Verteilung stammen (z.B. Daten sind Gaußsch verteilt). Aus dieser Annahme versuchen wir im Allgemeinen, die „Form“ der Daten zu definieren, und können abweichende Beobachtungen als Beobachtungen definieren, die weit genug von der angepassten Form entfernt sind.
scikit-learn stellt ein Objekt covariance.EllipticEnvelope zur Verfügung, das eine robuste Kovarianzschätzung an die Daten anpasst und somit eine Ellipse an die zentralen Datenpunkte anpasst, wobei Punkte außerhalb des zentralen Modus ignoriert werden.
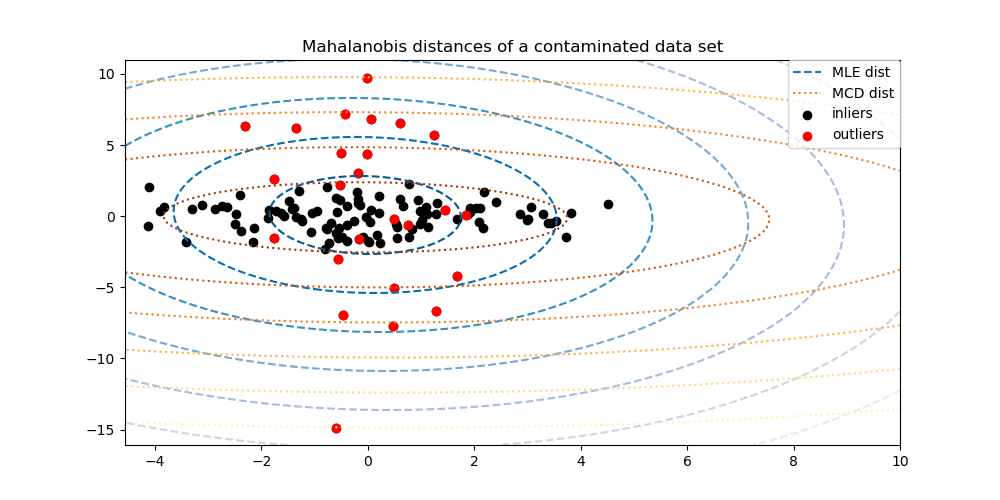
Wenn zum Beispiel angenommen wird, dass die Inlier-Daten Gaußsch verteilt sind, schätzt es die Inlier-Position und Kovarianz auf robuste Weise (d.h. ohne von Ausreißern beeinflusst zu werden). Die aus dieser Schätzung abgeleiteten Mahalanobis-Distanzen werden verwendet, um ein Maß für die Abweichung abzuleiten. Diese Strategie wird unten veranschaulicht.
Beispiele
Siehe Robuste Kovarianzschätzung und die Relevanz von Mahalanobis-Distanzen für eine Veranschaulichung des Unterschieds zwischen der Verwendung einer Standard- (
covariance.EmpiricalCovariance) oder einer robusten Schätzung (covariance.MinCovDet) von Position und Kovarianz zur Bewertung des Grads der Abweichung einer Beobachtung.Siehe Ausreißererkennung auf einem realen Datensatz für ein Beispiel zur robusten Kovarianzschätzung auf einem realen Datensatz.
Referenzen
Rousseeuw, P.J., Van Driessen, K. „A fast algorithm for the minimum covariance determinant estimator“ Technometrics 41(3), 212 (1999)
2.7.3.2. Isolation Forest#
Eine effiziente Methode zur Ausreißererkennung in hochdimensionalen Datensätzen ist die Verwendung von Zufallswäldern. Der ensemble.IsolationForest „isoliert“ Beobachtungen, indem er zufällig ein Merkmal auswählt und dann zufällig einen Split-Wert zwischen den Maximal- und Minimalwerten des ausgewählten Merkmals wählt.
Da die rekursive Partitionierung durch eine Baumstruktur dargestellt werden kann, entspricht die Anzahl der Teilungen, die zur Isolierung einer Stichprobe erforderlich sind, der Pfadlänge vom Wurzelknoten zum Endknoten.
Diese Pfadlänge, gemittelt über einen Wald solcher Zufallsbäume, ist ein Maß für die Normalität und unsere Entscheidungfunktion.
Zufällige Partitionierung erzeugt für Anomalien spürbar kürzere Pfade. Daher sind Proben, für die ein Wald von Zufallsbäumen gemeinsam kürzere Pfadlängen ergibt, mit hoher Wahrscheinlichkeit Anomalien.
Die Implementierung von ensemble.IsolationForest basiert auf einem Ensemble von tree.ExtraTreeRegressor. Nach dem ursprünglichen Isolation Forest-Papier ist die maximale Tiefe jedes Baumes auf \(\lceil \log_2(n) \rceil\) gesetzt, wobei \(n\) die Anzahl der Stichproben ist, die zum Aufbau des Baumes verwendet werden (siehe [1] für weitere Details).
Dieser Algorithmus wird unten veranschaulicht.
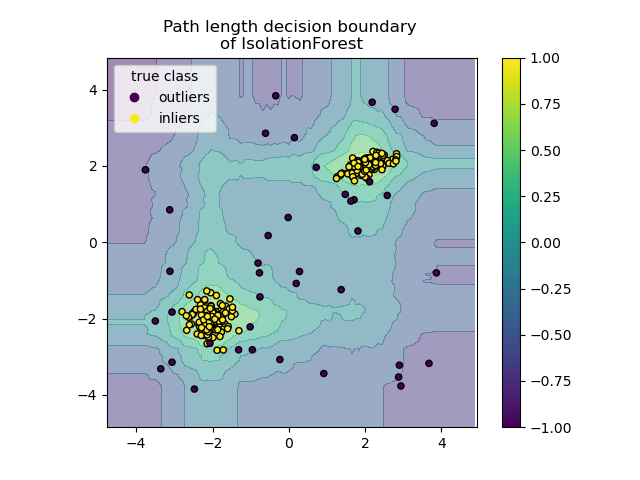
Der ensemble.IsolationForest unterstützt warm_start=True, was es Ihnen ermöglicht, einem bereits gefitteten Modell weitere Bäume hinzuzufügen.
>>> from sklearn.ensemble import IsolationForest
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [0, 0], [-20, 50], [3, 5]])
>>> clf = IsolationForest(n_estimators=10, warm_start=True)
>>> clf.fit(X) # fit 10 trees
>>> clf.set_params(n_estimators=20) # add 10 more trees
>>> clf.fit(X) # fit the added trees
Beispiele
Siehe IsolationForest-Beispiel für eine Veranschaulichung der Verwendung von IsolationForest.
Siehe Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Spielzeugdatensätzen für einen Vergleich von
ensemble.IsolationForestmitneighbors.LocalOutlierFactor,svm.OneClassSVM(optimiert für Ausreißererkennung),linear_model.SGDOneClassSVMund einer kovarianzbasierten Ausreißererkennung mitcovariance.EllipticEnvelope.
Referenzen
2.7.3.3. Local Outlier Factor#
Eine weitere effiziente Methode zur Ausreißererkennung in moderat hochdimensionalen Datensätzen ist die Verwendung des Local Outlier Factor (LOF)-Algorithmus.
Der neighbors.LocalOutlierFactor (LOF)-Algorithmus berechnet einen Score (genannt Local Outlier Factor), der den Grad der Abnormalität von Beobachtungen widerspiegelt. Er misst die lokale Dichteabweichung eines gegebenen Datenpunkts im Verhältnis zu seinen Nachbarn. Die Idee ist, Stichproben zu erkennen, die eine erheblich geringere Dichte als ihre Nachbarn aufweisen.
In der Praxis wird die lokale Dichte aus den k-nächsten Nachbarn ermittelt. Der LOF-Score einer Beobachtung entspricht dem Verhältnis der durchschnittlichen lokalen Dichte ihrer k-nächsten Nachbarn zu ihrer eigenen lokalen Dichte: Eine normale Instanz wird voraussichtlich eine lokale Dichte aufweisen, die der ihrer Nachbarn ähnelt, während abweichende Daten voraussichtlich eine viel geringere lokale Dichte aufweisen.
Die Anzahl k der betrachteten Nachbarn (Alias-Parameter n_neighbors) wird typischerweise gewählt 1) größer als die Mindestanzahl von Objekten, die ein Cluster enthalten muss, damit andere Objekte lokale Ausreißer in Bezug auf dieses Cluster sein können, und 2) kleiner als die maximale Anzahl nahegelegener Objekte, die potenziell lokale Ausreißer sein können. In der Praxis sind solche Informationen im Allgemeinen nicht verfügbar, und die Wahl von n_neighbors=20 scheint im Allgemeinen gut zu funktionieren. Wenn der Anteil der Ausreißer hoch ist (d.h. größer als 10 %, wie im folgenden Beispiel), sollte n_neighbors größer sein (n_neighbors=35 im folgenden Beispiel).
Die Stärke des LOF-Algorithmus liegt darin, dass er sowohl lokale als auch globale Eigenschaften von Datensätzen berücksichtigt: Er kann auch in Datensätzen, in denen abweichende Stichproben unterschiedliche zugrundeliegende Dichten aufweisen, gut funktionieren. Die Frage ist nicht, wie isoliert die Stichprobe ist, sondern wie isoliert sie im Verhältnis zur umgebenden Nachbarschaft ist.
Bei der Anwendung von LOF für die Ausreißererkennung gibt es keine Methoden predict, decision_function und score_samples, sondern nur eine fit_predict-Methode. Die Scores der Abnormalität der Trainingsstichproben sind über das Attribut negative_outlier_factor_ zugänglich. Beachten Sie, dass predict, decision_function und score_samples auf neuen, ungesehenen Daten verwendet werden können, wenn LOF für die Neuheitserkennung angewendet wird, d.h. wenn der Parameter novelty auf True gesetzt ist, das Ergebnis von predict jedoch vom Ergebnis von fit_predict abweichen kann. Siehe Neuheitserkennung mit Local Outlier Factor.
Diese Strategie wird unten veranschaulicht.
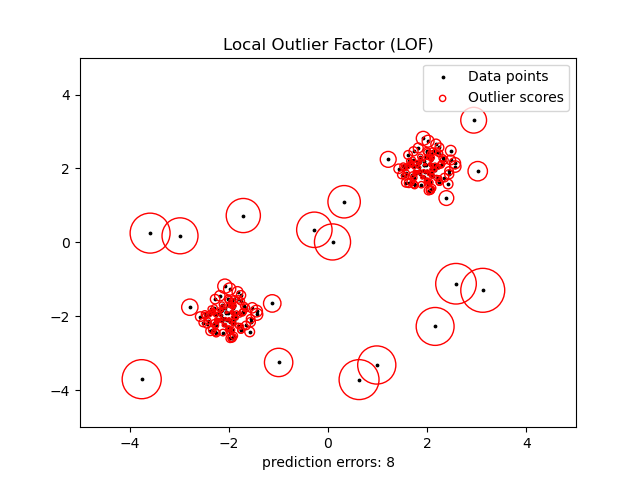
Beispiele
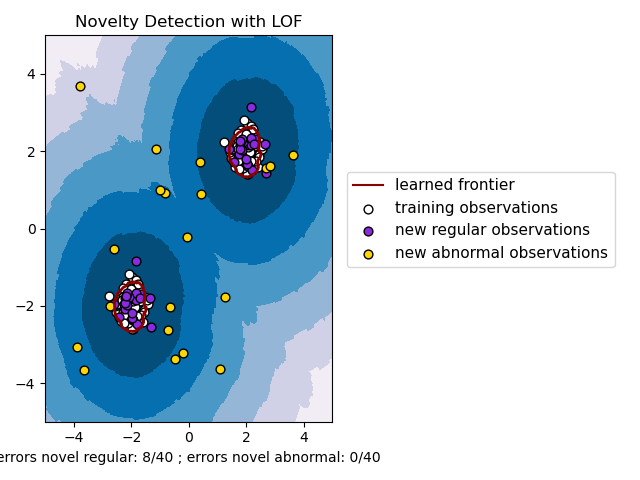
Siehe Ausreißererkennung mit Local Outlier Factor (LOF) für eine Veranschaulichung der Verwendung von
neighbors.LocalOutlierFactor.Siehe Vergleich von Anomalieerkennungsalgorithmen zur Ausreißererkennung auf Spielzeugdatensätzen für einen Vergleich mit anderen Anomalieerkennungsmethoden.
Referenzen
Breunig, Kriegel, Ng, und Sander (2000) LOF: identifying density-based local outliers. Proc. ACM SIGMOD
2.7.3.3. Local Outlier Factor#
Um neighbors.LocalOutlierFactor für die Neuheitserkennung zu verwenden, d.h. um Labels vorherzusagen oder den Score der Abnormalität neuer, ungesehener Daten zu berechnen, müssen Sie den Estimator mit dem Parameter novelty auf True setzen, bevor Sie den Estimator fitten.
lof = LocalOutlierFactor(novelty=True)
lof.fit(X_train)
Beachten Sie, dass fit_predict in diesem Fall nicht verfügbar ist, um Inkonsistenzen zu vermeiden.
Warnung
Neuheitserkennung mit Local Outlier Factor
Wenn novelty auf True gesetzt ist, beachten Sie, dass Sie predict, decision_function und score_samples nur auf neuen, ungesehenen Daten verwenden dürfen und nicht auf den Trainingsstichproben, da dies zu falschen Ergebnissen führen würde. D.h., das Ergebnis von predict wird nicht dasselbe sein wie das von fit_predict. Die Scores der Abnormalität der Trainingsstichproben sind immer über das Attribut negative_outlier_factor_ zugänglich.
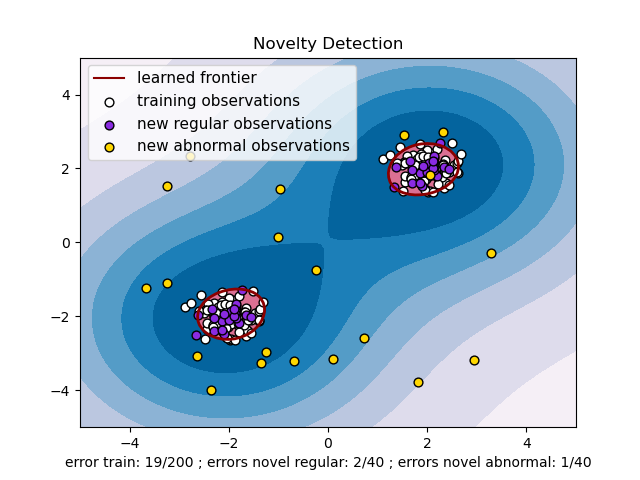
Die Neuheitserkennung mit neighbors.LocalOutlierFactor wird unten veranschaulicht (siehe Neuheitserkennung mit Local Outlier Factor (LOF)).